How Do You Simplify (1 - Tan²x) / (1 + Tan²x)
Trigonometric identities are equations involving trigonometric functions that hold true for all possible values of the variables within their respective domains. These identities are derived from the geometric relationships and properties of right triangles, circles, and periodic functions. In this article, we will derive one such trigonometric identity by simplifying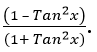
What are Trigonometric Ratios
Trigonometric ratios are mathematical functions that relate the angles of a right triangle to the ratios of the lengths of its sides. In trigonometry, there are six primary trigonometric ratios,namely sine, cosine, tangent, cosecant, secant, and cotangent. These
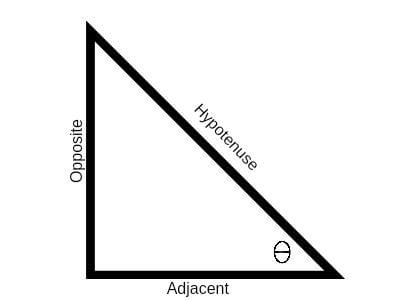
ratios are often abbreviated as sin, cos, tan, csc, sec, and cot, respectively.
The tangent function is denoted as "Tan" and is defined as follows:
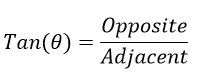
The sine function is denoted as "Sin" and is defined as follows:
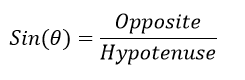
The cosine function is denoted as "Cos" and is defined as follows:
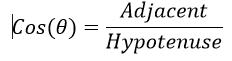
Here, theta represents the angle, and the opposite and adjacent sides refer to the sides of the right triangle relative to the angle.
What Is (1 - Tan²x) / (1 + Tan²x)
Mathematically, (1 - Tan²x) / (1 + Tan²x) can be expressed as:
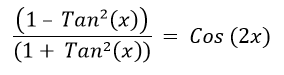
This identity provides a way to express the tangent of an angle in terms of its cosine. It helps simplify trigonometric expressions by replacing the tangent of an angle with the cosine of the angle.
Explanation
To prove that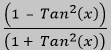 is equal to Cos (2x), we can start with the left side of the equation and manipulate it using trigonometric identities until we arrive at the right side. Here's a step-by-step explanation: is equal to Cos (2x), we can start with the left side of the equation and manipulate it using trigonometric identities until we arrive at the right side. Here's a step-by-step explanation:
- Step 1: Start with the left side of the equation:
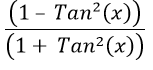
- Step 2: Use the identity Tan2 (x) + 1 = Sec2 (x) to rewrite the denominator:
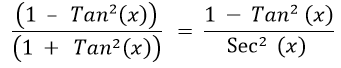
- Step 3: Use the identity Tan2 (x)=
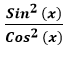 to rewrite the numerator: to rewrite the numerator:
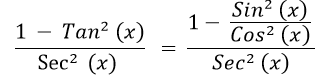
- Step 4: Use the identity Sin2 (x)+ Cos2 (x) = 1 to rewrite the numerator:
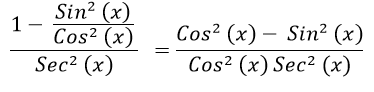
- Step 5: Use the identity Sec2 (x)=
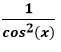 to simplify the denominator: to simplify the denominator:
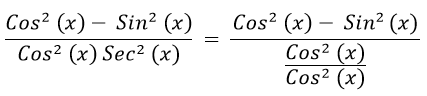
- Step 6: Cancel out Cos2(x) in the denominator:
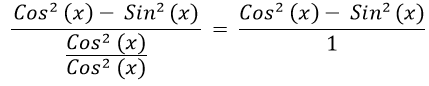
- Step 7: Use the identity Cos2(x) - Sin2(x) = Cos(2x) to rewrite the numerator:
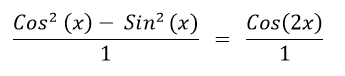
- Step 8: Simplify the expression by removing the denominator:
Thus, we have proved that  is equal to Cos (2x) by stepwise manipulation of the equation. is equal to Cos (2x) by stepwise manipulation of the equation.
Uses of Trigonometric Identities
The trigonometric identities are immensely useful in trigonometry, calculus, and physics.
- They can be used to solve trigonometric equations by transforming them into simpler forms. By substituting
 with Cos (2x) , equations can be rewritten in terms of a single variable for easier solving. with Cos (2x) , equations can be rewritten in terms of a single variable for easier solving.
- Trigonometric identities aids in simplifying complex trigonometric expressions involving multiple angles. Repeatedly applying the trigonometric identities can reduce the number of angles and terms in an expression, enhancing clarity and facilitating further analysis.
- In calculus, trigonometric identities allow for the transformation of trigonometric functions into simpler forms. This simplification enables the application of integration and differentiation rules, helping to solve differential equations, evaluate integrals, and derive mathematical models in physics and engineering.
- Geometrically, the trigonometric identities help analyze angles and their relationships within shapes and figures. It allows for relating angles to their double angles, enabling exploration of symmetry, congruence, and similarity in geometric configurations.
- Trigonometric identities assist in solving problems involving angles in triangles, quadrilaterals, and other polygons.
- In physics, trigonometric identities are extensively used in wave mechanics, oscillations, and vibrations. It helps describe the behavior of waves, such as light and sound, by relating the angles of incidence and reflection.
- Trigonometric identities also play a crucial role in analyzing the phase difference between waves and determining interference patterns.
Conclusion
 = Cos (2x) is a fundamental trigonometric identity that relates the tangent function to the cosine of the angle. It serves as a powerful tool in trigonometry, calculus, and physics, facilitating the simplification of expressions, solving equations, and analyzing geometric and wave-related problems. Its versatility and wide range of applications make it an essential concept for anyone studying or working with trigonometry and its related fields. = Cos (2x) is a fundamental trigonometric identity that relates the tangent function to the cosine of the angle. It serves as a powerful tool in trigonometry, calculus, and physics, facilitating the simplification of expressions, solving equations, and analyzing geometric and wave-related problems. Its versatility and wide range of applications make it an essential concept for anyone studying or working with trigonometry and its related fields.
|

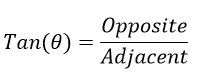
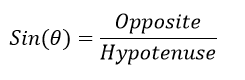
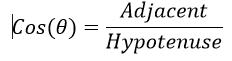
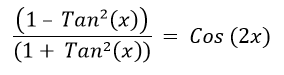
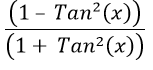
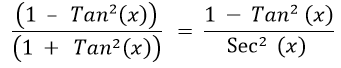
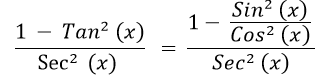
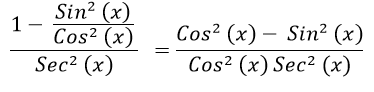
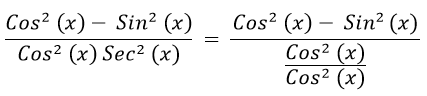
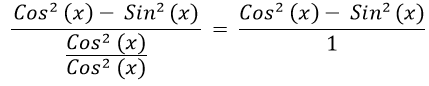
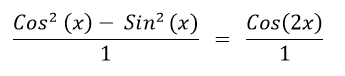
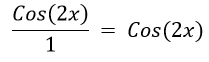
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now





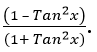
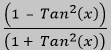 is equal to Cos (2x), we can start with the left side of the equation and manipulate it using trigonometric identities until we arrive at the right side. Here's a step-by-step explanation:
is equal to Cos (2x), we can start with the left side of the equation and manipulate it using trigonometric identities until we arrive at the right side. Here's a step-by-step explanation: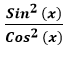 to rewrite the numerator:
to rewrite the numerator: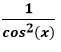 to simplify the denominator:
to simplify the denominator: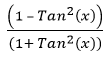 is equal to Cos (2x) by stepwise manipulation of the equation.
is equal to Cos (2x) by stepwise manipulation of the equation.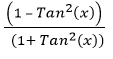 with Cos (2x) , equations can be rewritten in terms of a single variable for easier solving.
with Cos (2x) , equations can be rewritten in terms of a single variable for easier solving.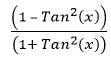 = Cos (2x) is a fundamental trigonometric identity that relates the tangent function to the cosine of the angle. It serves as a powerful tool in trigonometry, calculus, and physics, facilitating the simplification of expressions, solving equations, and analyzing geometric and wave-related problems. Its versatility and wide range of applications make it an essential concept for anyone studying or working with trigonometry and its related fields.
= Cos (2x) is a fundamental trigonometric identity that relates the tangent function to the cosine of the angle. It serves as a powerful tool in trigonometry, calculus, and physics, facilitating the simplification of expressions, solving equations, and analyzing geometric and wave-related problems. Its versatility and wide range of applications make it an essential concept for anyone studying or working with trigonometry and its related fields.




