Bessel Function in MATLAB

In MATLAB, Bessel functions are a family of mathematical functions that are part of the special functions toolbox. These functions are named after Friedrich Bessel and are solutions to Bessel's differential equation. MATLAB provides several Bessel functions, each serving different purposes in various applications, such as physics, engineering, and signal processing.

Here are some of the main Bessel functions available in MATLAB:

Bessel Function of the First Kind (besselj):

Computes the Bessel function of the first kind, denoted as J?(X), where nu is the order of the Bessel function, and X is the input.

Bessel Function of the Second Kind (bessely):

Computes the Bessel function of the second kind, denoted as Y?(X), where nu is the order of the Bessel function, and X is the input.

Modified Bessel Function of the First Kind (besseli):

Computes the modified Bessel function of the first kind, denoted as I?(X), where nu is the order of the Bessel function, and X is the input.

Modified Bessel Function of the Second Kind (besselk):

Computes the modified Bessel function of the second kind, denoted as K?(X), where nu is the order of the Bessel function, and X is the input.

Hankel Function of the First Kind (besselh):

Computes the Hankel function of the first kind, denoted as H?(X), where nu is the order, kind specifies the kind of Hankel function, and X is the input.

These functions are essential in solving problems involving circular or cylindrical symmetry, such as wave propagation, heat conduction, and vibration analysis.
They are valuable tools for researchers and engineers working on diverse scientific and engineering applications.

Starting with the Fundamentals

Embracing the Basics of Bessel Functions

To understand Bessel functions, it's imperative to start with their fundamental forms. MATLAB, a versatile numerical computing environment, offers convenient access to these functions, simplifying their integration into various computational tasks.

The Primary Players: Jν(x) and Yν(x)

Two essential entities lie at the core of Bessel functions: the primary Bessel function of the first kind, represented as Jν(x), and its counterpart, the Bessel function of the second kind, denoted as Yν(x).

These functions are foundational components that form the basis for more complex variations and applications.

The Primary Bessel Function (Jν(x))

The Bessel function of the first kind, Jν(x), is a solution to Bessel's differential equation. It describes oscillatory behavior, often encountered in problems with circular or cylindrical symmetry.

In MATLAB, generating and manipulating Jν(x) is as straightforward as calling the besselj function.

Example:

% Generating Bessel Function J?(x)
x_values = linspace(0, 10, 100);
nu = 1; % Order of Bessel Function
J_nu_values = besselj(nu, x_values);

% Displaying the Result
figure;
plot(x_values, J_nu_values);
title('Primary Bessel Function J_1(x)');
xlabel('x');
ylabel('J_1(x)');

Output:

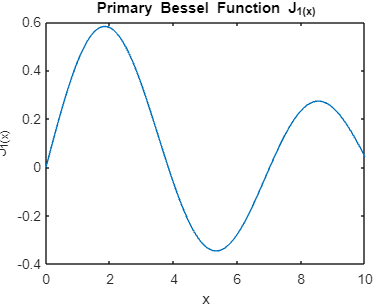
Explanation:

Generate x-values: linspace(0, 10, 100) creates an array of 100 equally spaced values between 0 and 10. These values represent the variable x for which the Bessel function will be calculated.

Set the order of the Bessel function: nu = 1 specifies the order ν of the Bessel function. In this case, it's set to 1, so the code is generating the Bessel function 1J1 (x).

Calculate Bessel function values: besselj(nu, x_values) calculates the values of the Bessel function Jν (x) for the specified order ν and the array of x-values.

The Bessel Function of the Second Kind (Yν(x))

Complementing Jν(x), the Bessel function of the second kind, Yν(x), provides another perspective on oscillatory phenomena.

It also arises as a solution to Bessel's differential equation but exhibits different behavior, particularly near the origin.
MATLAB's bessely function facilitates the exploration of Yν(x).

Example:

% Generating Bessel Function Y?(x)
x_values = linspace(0, 10, 100);
nu = 1; % Order of Bessel Function
Y_nu_values = bessely(nu, x_values);

% Displaying the Result
figure;
plot(x_values, Y_nu_values);
title('Bessel Function of the Second Kind Y_1(x)');
xlabel('x');
ylabel('Y_1(x)');

Output:

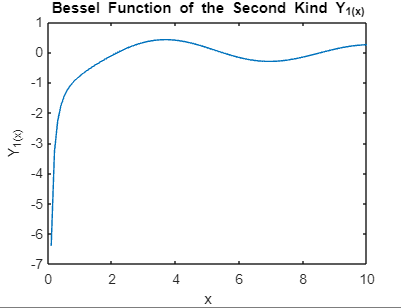
Understanding Orders and Arguments

The order (ν) and argument (x) of Bessel functions play a pivotal role in shaping their behavior.

Exploring different orders and arguments provides insights into the diverse applications of these functions across various mathematical scenarios.

Exploring the Mathematical Landscape

Bessel Functions: A Mathematical Marvel

These functions are known for their appearance in solutions to partial differential equations, making them indispensable in diverse scientific and engineering domains.

Versatility in Problem Solving

Bessel functions are characterized by their versatility in solving mathematical problems, especially those involving wave propagation, diffusion phenomena, and circular symmetry.

Crucial Role in Physics

In the realm of physics, Bessel functions frequently arise when dealing with problems featuring cylindrical or spherical symmetry.
For instance, when studying wave propagation in circular or spherical geometries, Bessel functions naturally emerge as solutions to the associated differential equations.

Engineering Applications

Engineers leverage Bessel functions to address a myriad of problems, particularly those involving cylindrical structures and vibrations.
The functions' ability to describe oscillatory behavior in these scenarios makes them invaluable in the analysis and design of mechanical systems, antennas, and resonant structures.

Signal Processing Significance

Signal processing stands as another domain where Bessel functions leave a profound impact.
Their role in filter design, especially in the creation of Bessel filters, highlights their significance.
Bessel filters are known for their maximally flat group delay, making them ideal for applications where maintaining the timing relationships among different frequency components is crucial.

Unveiling the Complexity with MATLAB

Its built-in functions allow researchers, scientists, and engineers to seamlessly integrate Bessel functions into their workflows, simplifying complex mathematical tasks in various disciplines.

Special Cases and Applications

Diving Deeper into Bessel Functionality

Bessel functions, with their distinctive properties for varying orders and arguments, hold a significant place in mathematical analysis. Understanding these nuances is crucial for their effective application in solving real-world problems. Let's explore special cases and delve into practical applications.

Zeroth-Order Bessel Function (J0(x))

One of the key special cases is the zeroth-order Bessel function, denoted as J0(x). This function represents circular symmetry and finds applications in scenarios where radial symmetry is paramount. In fields like heat conduction and vibration analysis, J0(x) emerges as a fundamental solution.

Example:

% Zeroth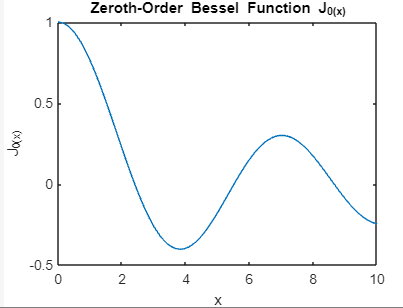-Order Bessel Function
x_values = linspace(0, 10, 100);
J0_values = besselj(0, x_values);

% Displaying the Result
figure;
plot(x_values, J0_values);
title('Zeroth-Order Bessel Function J_0(x)');
xlabel('x');
ylabel('J_0(x)');

Output:

Visualizing Bessel Functions

Enhancing Comprehension through Visualization

Visual representation plays a pivotal role in comprehending the intricate behavior of Bessel functions. MATLAB's powerful plotting capabilities allow us to create visually appealing representations, aiding in the interpretation of their oscillatory patterns.

Example:

% Visual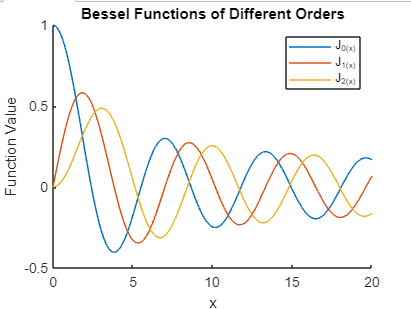ization of Bessel Functions
x = linspace(0, 20, 200);
nu_values = [0, 1, 2];

figure;
hold on;
for nu = nu_values
    J_nu = besselj(nu, x);
    plot(x, J_nu, 'DisplayName', ['J_' num2str(nu) '(x)']);
end

title('Bessel Functions of Different Orders');
xlabel('x');
ylabel('Function Value');
legend('show');

Output:

In this visualization, different orders of Bessel functions (Jν(x)) are displayed, providing a clear depiction of their oscillatory nature.

This visual exploration enhances our understanding of how these functions behave across varying values of x and order ν.

Advanced Applications

Bessel Functions in Signal Processing

In the realm of advanced applications, Bessel functions demonstrate their prowess in signal processing, specifically in the design of filters.

The unique properties of Bessel functions contribute to the creation of filters with specific and desirable frequency responses.

Example:

% Signal Processing with Bessel Functions
n = 4; % Filter Order
wc = 0.5; % Cutoff Frequency

[b, a] = besself(n, wc);
freqz(b, a);
title('Frequency Response of Bessel Filter');

Output:

Bessel filters, designed using Bessel functions, hold a distinctive advantage in signal processing due to their maximally flat group delay.
This characteristic makes them well-suited for applications where maintaining the timing relationships among different frequency components is critical.
Exploration into Bessel functions reveals that these mathematical tools are not merely theoretical entities but have practical significance, especially in MATLAB.

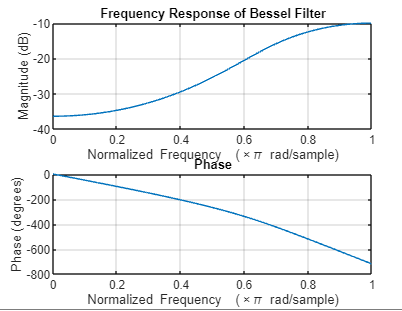
Their versatility spans across physics, engineering, and signal processing, making them indispensable for solving complex problems, few use-cases are:

Antenna Design and Radiation Patterns

Bessel functions play a crucial role in antenna design, especially when dealing with circular or cylindrical structures. The mathematical description provided by Bessel functions aids in analyzing and optimizing radiation patterns, ensuring efficient and precise antenna performance.

Acoustic Modeling and Vibrations

In acoustics and vibration analysis, Bessel functions find applications in describing the vibrational modes of circular and cylindrical structures. These functions help model the resonance frequencies and mode shapes, enabling engineers to design structures with desired acoustic properties and minimal vibration.

Heat Conduction in Cylindrical Systems

The study of heat conduction in cylindrical systems often involves Bessel functions. Their solutions to the heat equation provide insights into temperature distributions and heat transfer mechanisms in cylindrical geometries, which are particularly valuable in thermal analysis and the design of cooling systems.

Quantum Mechanics and Wave Functions

Bessel functions appear in the solutions of Schrödinger's equation in quantum mechanics. They play a vital role in describing the wave functions of particles in circular or cylindrical potentials, contributing to our understanding of quantum states and energy levels.

Bessel-Fourier Transformations

Bessel functions are intricately linked to Fourier transformations in problems with cylindrical symmetry. The Bessel-Fourier transform is employed in solving partial differential equations involving cylindrical coordinates, facilitating the analysis of phenomena such as diffraction and wave propagation.

Bessel Filters in Signal Processing

As previously mentioned, Bessel functions find extensive use in signal processing, particularly in the design of Bessel filters. These filters are favored for applications where maintaining the timing relationships among different frequency components is critical, such as in audio processing and telecommunications.

Plasma Physics and Fusion Research

In plasma physics and fusion research, Bessel functions emerge to describe the behavior of plasma waves and oscillations. Understanding these functions is essential for predicting and controlling the dynamics of plasma in fusion reactors.

Medical Imaging and Tomography

Bessel functions contribute to the mathematical models used in medical imaging, especially in tomography. Their applications aid in reconstructing images from projection data, allowing for detailed and accurate diagnostic imaging in fields like computed tomography (CT) scans.

In essence, the advanced applications of Bessel functions underscore their indispensable role in solving complex problems across diverse scientific and engineering disciplines.
Their mathematical elegance and ability to describe phenomena in circular and cylindrical geometries make them a valuable tool in the hands of researchers and practitioners pushing the boundaries of knowledge and technology.

Example:

% Antenna Design and Radiation Patterns

% Parameters
radius = 0.5; % Radius of the circular antenna array
num_elements = 8; % Number of antenna elements
theta = linspace(0, 2*pi, 360); % Angular range for radiation pattern

% Bessel Function for Radiation Pattern
J_nu = @(nu, kr) besselj(nu, kr); % Bessel function handle

% Calculate Radiation Pattern
radiation_pattern = zeros(size(theta));
for nu = 0:2 % Example: Considering the first three orders
    kr = (2*pi*radius /1) * sin(theta); % kr is the product of wavenumber and radius
    radiation_pattern = radiation_pattern + abs(J_nu(nu, kr)).^2;
end

% Normalize the Radiation Pattern
radiation_pattern = radiation_pattern / max(radiation_pattern);

% Plotting the Radiation Pattern
figure;
polarplot(theta, radiation_pattern, 'LineWidth', 2);
title('Circular Antenna Array Radiation Pattern');

Output:

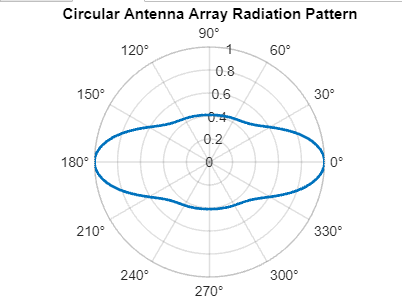
In this implementation:

The circular antenna array is defined with a specified radius and number of elements. Bessel functions are utilized to calculate the radiation pattern for each antenna element.
The radiation patterns for different Bessel function orders (ν) are considered and summed up. The resulting radiation pattern is normalized for visualization.
The polar plot is used to depict the radiation pattern in a circular context.

Explanation:

This example illustrates how Bessel functions can be employed in the context of antenna design, providing insights into the radiation characteristics of a circular antenna array.

Actual implementations would vary based on the specific requirements and mathematical models relevant.
The chosen application, whether it be in acoustics, heat conduction, quantum mechanics, or any other field where Bessel functions find application.

Advantages and Disadvantages

Advantages of Bessel Functions	Disadvantages of Bessel Functions
Mathematical Elegance: Bessel functions exhibit elegant mathematical properties, facilitating their use in various differential equations.	Limited Applicability: Bessel functions are specifically tailored for problems with circular or cylindrical symmetry, limiting their scope in other geometries.
Versatility: Bessel functions find applications across diverse scientific and engineering domains, making them a powerful tool for solving a wide range of problems.	Complexity in Higher Orders: Higher-order Bessel functions can exhibit intricate behavior, and their mathematical expressions may become more complex.
Orthogonality: Bessel functions are orthogonal over specific intervals, simplifying their use in Fourier series expansions and integral transforms.	Numerical Stability: Numerical instability may arise when computing Bessel functions, especially with high orders or extreme values of arguments.
Representation of Oscillatory Phenomena: Bessel functions naturally describe oscillatory behavior in systems with circular or cylindrical symmetry.	Boundary Conditions: Bessel functions are often solutions to homogeneous differential equations, and specific boundary conditions must be applied to match the physical problem.
Bessel's Differential Equation Solutions: Bessel functions arise as solutions to Bessel's differential equation, providing insights into complex physical phenomena.	Limited Direct Physical Interpretation: While Bessel functions provide mathematical solutions to problems, their direct physical interpretation may only sometimes be intuitive.