Numerical Integration (Quadrature)

A numerical evaluation of the integral ∫ f(x)dx is known as Quadrature.

The general form of numerical integration of a function f (x) over some interval [a, b] is a weighted total of the function values at a finite number (N + 1) of sample points (nodes), indicated to as 'quadrature':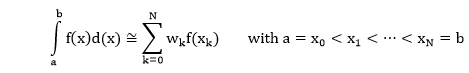

MATLAB provides built-in functions for numerical integration:

quad

It integrates a specified function over specified limits, build on adaptive Simpson's rule. The adaptive rule follows to improve accuracy by adaptively selecting the estimate of the subintervals within the limits of integrations while evaluating the sums that make up the integral.

quadl

It integrates a specified function over specified limits, build on adaptive Lobatto quadrature. This one is more accurate than a quad, but it also uses more function evaluations.

The syntax for both quad and quad1 are as follows: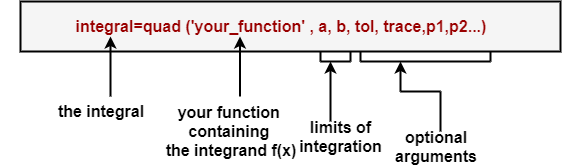

To use quad1, you replace quad with quad1 in the syntax. As shown in syntax, both functions require us to supply the integrand as a userwritten function.

The optional input argument tol specifies absolute tolerance (default value is 10^-6). A nonzero value of the other optional argument, trace, shows some intermediate calculations at each step.

The optional arguments p1, p2, etc., are passed on to the user-defined function as input arguments in addition to x.

The steps include in numerical integration using these built-in functions are:

Step1: Write a function that returns the value of the integrand f(x) given the value of x. Our function should be able to accept the input value x as a vector and produce the value of the integrand (the output) as a vector.

Step2: It decides which function to use -quad or quad1(quad is faster but less accurate than quad1). The default tolerance value is 10^-6 Find the Integral.

Example

Let us compute the following Integral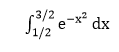

This integration is closely related to the error function, erf.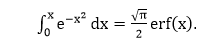

MATLAB also provides the error function, erf, as a built-in function, we can evaluate our integral in closed form (in terms of the error function) and compare the results from numerical integration. Let us follow the steps outlined previously.

Step1: Here is the function that evaluates the integrand at given x (x is allowed to be a vector).

Step2: Let us use quad with its simplest syntax:

The exact result for the integral, up to 10 decimal places, is 0.3949073872. In the preceding example, we have used the default tolerance. Here is a table showing the results of a few experiments with the integral. We use both quad and quad1 for integration. For a quad, we tabulate results with different tolerances. In the table, we list the value of the integral, % error, and the number of function evaluations. For quad1 gives quite an accurate solution with just the default tolerance.