MATLAB Inverse Function

Introduction

In MATLAB, the identity matrix, commonly abbreviated as I is produced by multiplying the inverse of a matrix, denoted as A1, by the original matrix A. Many scientific and technical applications require the ability to compute the inverse of a matrix, which enables researchers and practitioners to solve challenging mathematical issues quickly and accurately.

The inverse function in MATLAB is explored in-depth in this article, along with insights into its syntax, uses, and best practices for utilizing this crucial tool in numerical computation and data analysis.

• Users can manipulate matrices, solve linear equations, and engage in complex mathematical analyses with confidence and accuracy by grasping the nuances of the MATLAB inverse function.
• The inverse of a matrix A is known as A1 in linear algebra. The identity matrix, indicated as I is produced when this inverse matrix is multiplied by the original matrix A.
• The identity matrix is a square matrix with zeros everywhere else and ones on the main diagonal.

In mathematics, the identity matrix is the result of a matrix and its inverse:

In many mathematical operations, such as resolving systems of linear equations, identifying eigenvalues and eigenvectors, and carrying out transformations, computing the inverse of a matrix is a crucial step.

• MATLAB's 'inv' function is intended exclusively for calculating a matrix's inverse.

The 'inv' function in MATLAB has a simple syntax for use.

If we have a matrix A, then the instruction to obtain A's inverse is:

Additionally, MATLAB offers several tools and functions for resolving linear equation systems and computing matrices.

• The 'inv' function is one way to determine a matrix's inverse. However, it is only sometimes the fastest or most accurate approach.
• The backslash operator (''), which MATLAB provides, is preferred over the 'inv' function for solving systems of linear equations because of its computational effectiveness and numerical stability.

Inv Function;

The 'inv' function may not produce correct results when working with big and complicated matrices because of numerical instability or precision problems. Applying more sophisticated techniques, like the LU or QR decomposition, can offer more dependable and effective answers in these situations. Because MATLAB has built-in functions for various operations, users can select the most effective technique based on the unique properties of the matrices in question.

Consider the following example to show how the MATLAB 'inv' function is used:

Output: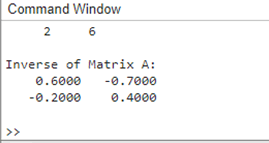

The original matrix A and its matching inverse are shown when this code is run in MATLAB. The accuracy and effectiveness of matrix computations in MATLAB can be greatly improved by being aware of the characteristics and restrictions of the "inv" function.

eigenvalues and eigenvectors:

MATLAB supports complicated mathematical issues, such as eigenvalue and eigenvector computations and simple matrix operations. A matrix's eigenvalues and eigenvectors are essential in many applications, including signal processing, data compression, and stability analysis. MATLAB's 'eig' function can calculate a matrix's eigenvalues and eigenvectors.

It is simple to use the 'eig' function in MATLAB. The command to determine the eigenvalues and eigenvectors of a matrix B is:

Additionally, MATLAB provides a wide range of visualization tools for displaying data and mathematical operations. Understanding large, complicated data sets and mathematical models requires visualization. Line plots, scatter plots, bar plots, surface plots, and other plots can all be created using MATLAB's functions.

Example:

Output: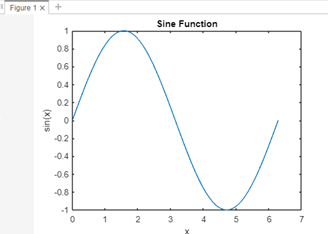

When this code is run in MATLAB, a plot of the sine function throughout the range [0, 2] is produced. To generate visually appealing and useful visualizations, users can modify several characteristics, including line styles, colors, markers, and axis features, using MATLAB's full customization tools for plots.

The inverse function is an essential tool for carrying out numerous mathematical computations and analyses in MATLAB. Users may effectively manage difficult mathematical tasks and visualize data by understanding its application and other crucial MATLAB functions. A sophisticated and adaptable platform for numerical computing and data analysis across a wide range of fields, MATLAB has a robust set of features and operations.