MATLAB Derivatives

Introduction:

MATLAB, a prominent numerical computing environment, stands as a go-to tool for engineers, scientists, and researchers. One of its cornerstone capabilities lies in the realm of derivatives, a fundamental concept in calculus that measures how a function changes concerning its input. In this extensive exploration,

we embark on a journey through the intricacies of derivatives in MATLAB, covering both symbolic and numerical approaches. By the end, you will not only grasp the underlying mathematical principles but also wield the practical skills to compute derivatives efficiently.

Understanding Derivatives

Unraveling the Dynamics

At the heart of calculus lies the profound concept of derivatives, which serves as a fundamental tool for understanding how a function evolves. The essence of derivatives lies in quantifying the rate of change of a function, providing insights into how the function behaves at any given point. This concept holds immense significance across diverse fields, transcending disciplinary boundaries from physics to finance.

• In the realm of physics, derivatives help describe the motion of objects, detailing how velocity changes concerning time or how acceleration varies.
• In finance, derivatives play a pivotal role in risk management, helping to evaluate how financial instruments' values fluctuate with market dynamics.
• The ability to comprehend and harness derivatives is, therefore, a cornerstone skill for professionals navigating complex and dynamic systems.

MATLAB, with its robust computational capabilities, stands as an invaluable ally in unraveling the dynamics encapsulated within derivatives. Not only does it provide a platform for understanding the theoretical underpinnings of derivatives, but it also offers precise tools for their computational exploration.

Decoding the Derivative Notation

Mathematically, the derivative of a function f(x) is a measure of how the function's output changes concerning its input variable x. This instantaneous rate of change is denoted as f?(x) or dxdf, and it encapsulates a wealth of information about the function's behavior at a specific point.

• Breaking down the notation, f?(x) signifies the first derivative of with respect to x. It captures the slope of the tangent line to the graph of f at any given point, providing a visual representation of the function's rate of change.
• Alternatively, dxdf reinforces the idea that the derivative is obtained by considering the infinitesimally small change (dx) in the input variable and the resulting change (df) in the function's output.

Understanding this mathematical representation is crucial for interpreting and utilizing derivatives in various applications. It lays the foundation for both symbolic and numerical approaches to computing derivatives in MATLAB.

Symbolic Differentiation

Beyond Notation

MATLAB's Symbolic Math Toolbox elevates the understanding of derivatives beyond symbolic notation. It allows users to work with mathematical expressions as entities themselves rather than numerical values. Through this toolbox, users can manipulate and analyze derivatives symbolically, gaining a more profound insight into the underlying mathematical structures.

• For instance, consider a scenario where a function is represented symbolically, and its derivative needs to be obtained.
• MATLAB's symbolic differentiation functions, such as diff(), provide a direct pathway to compute the derivative without resorting to numerical approximations.
• This ensures precision and fidelity to the mathematical representation of derivatives.

Bridging Continuity with Discreteness

While symbolic approaches offer a deep understanding of derivatives, numerical computation in MATLAB provides the bridge between the continuous world of mathematics and the discrete reality of computing. Finite difference methods, readily available in MATLAB, enable the approximation of derivatives when analytical expressions are not feasible.

• MATLAB's numerical capabilities shine when dealing with real-world data, enabling the computation of derivatives from discrete measurements.
• Whether employing forward, backward, or central differences, MATLAB offers versatile tools to navigate the nuances of numerical differentiation, ensuring accuracy even in the presence of noisy data.

Bridging Theory and Computation

Numerical differentiation in MATLAB is a crucial technique for approximating derivatives when analytical solutions are impractical or when dealing with discrete data. This section will comprehensively explore the methods, strategies, and MATLAB functions involved in numerical differentiation.

Implementation:

Output:

Explanation:

rng(1);: Sets the random seed for reproducibility, ensuring the same random numbers are generated each time the program runs.

linspace(0, 2*pi, 100): Creates a linearly spaced vector x_numeric with 100 points between 0 and 2*pi.

y_numeric_noisy = sin(x_numeric) + 0.3 * randn(size(x_numeric));: Generates a sinusoidal function with added random noise to simulate real-world noisy data.

dy_dx_numeric_diff = diff(y_numeric_noisy) ./ diff(x_numeric);: Computes numerical derivatives using the diff function, representing the discrete approximation of the derivative.

Finite Difference Methods

Forward Difference:

The forward difference method approximates the derivative by considering the slope between a point and a point slightly ahead in the domain. In MATLAB, this is achieved using the diff function, which calculates the difference between consecutive elements in a vector.

Backward Difference

Conversely, the backward difference method calculates the slope between a point and a point slightly behind in the domain. The implementation is similar to the forward difference, with a slight modification.

Central Difference

The central difference method strikes a balance by considering points on both sides of the target point. This results in a more accurate approximation, especially for functions with rapid changes.

MATLAB Functions for Numerical Differentiation

Diff Function

The diff function in MATLAB is a versatile tool for numerical differentiation. It calculates the difference between consecutive elements in a vector and is a fundamental component in implementing finite difference methods.

Gradient Function

The gradient function in MATLAB extends the capabilities of diff by allowing users to compute gradients for multi-dimensional arrays. It provides a powerful tool for numerical differentiation in various scientific and engineering applications.

Handling Noisy Data

Real-world data is often subject to noise, which can adversely impact the accuracy of numerical differentiation. MATLAB provides several techniques to mitigate the effects of noise, enhancing the reliability of derivative computations.

Smoothing Techniques

Applying smoothing techniques, such as convolutions with a kernel or using the smooth data function, can help reduce the impact of noise on numerical derivatives.

Curve Fitting

Curve fitting using MATLAB's fit functions or other regression techniques can be employed to model the underlying trend in noisy data, facilitating more accurate numerical differentiation.

Implementation:

Navigating Noisy Data

In the realm of real-world data analysis, noise is an ever-present challenge that can significantly impact the accuracy of numerical differentiation. MATLAB, with its diverse set of tools and functions, provides robust strategies for handling noisy data, ensuring that the computed derivatives remain reliable and accurate. This section delves into the intricacies of navigating noisy data in MATLAB, offering insights into strategies for filtering and mitigating noise.

Understanding Noise in Data

Noise in data can manifest as random fluctuations or unwanted variations that distort the underlying signal. This phenomenon is particularly common in experimental measurements, sensor readings, or any data acquisition process influenced by external factors. When computing derivatives from such noisy data, the challenge lies in distinguishing between the genuine signal and the undesired noise.

Filtering Techniques

Moving Average Filtering

One fundamental technique for handling noisy data is the application of moving average filters. MATLAB provides a simple and effective way to smooth data using the smooth data function, allowing users to apply a moving average filter to reduce high-frequency noise.

Savitzky-Golay Filtering

The Savitzky-Golay filter, available in MATLAB, is another effective tool for noise reduction. It performs smoothing and differentiation simultaneously, preserving important features of the signal.

Curve Fitting for Noise Reduction

Curve fitting is a powerful technique to model the underlying trend in noisy data. MATLAB's fit functions, coupled with various fitting options, allow users to fit a smooth curve to the data, enabling more accurate derivative computations.

Robust Derivative Computation

Once the data has been preprocessed using filtering or curve fitting techniques, robust derivative computation becomes crucial. MATLAB's numerical differentiation methods, such as the forward, backward, or central difference methods, can be applied to the preprocessed data to obtain reliable derivatives.

Visualization and Evaluation

Visualizing the original noisy data, the filtered or fitted data and the computed derivatives is essential for evaluating the effectiveness of the noise reduction techniques. MATLAB's plotting functions enable users to create clear visualizations, facilitating a comprehensive analysis of the data processing pipeline.

Implementation:

Output: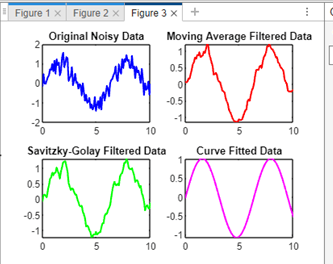

Explanation:

• Generate example noisy data: We create a sinusoidal signal with added random noise.
• Moving Average Filtering: We use the smoothdata function with a moving average filter.
• Savitzky-Golay Filtering: We use the sgolayfilt function for Savitzky-Golay filtering.
• Curve Fitting: We perform curve fitting using MATLAB's curve fitting toolbox.
• Robust Derivative Computation: We calculate the derivative using the gradient function.
• Visualization and Evaluation: We create two plots to visualize the original data, the filtered or fitted data, and the computed derivatives.

Advanced Techniques and Applications:

Symbolic Computation of Higher-Order Derivatives

In MATLAB, the computation of higher-order derivatives is facilitated by both symbolic and numerical methods. Symbolic computation allows for an elegant representation of higher-order derivatives, providing a deeper understanding of the mathematical intricacies. The diff function in MATLAB's Symbolic Math Toolbox can be employed to compute higher-order derivatives symbolically.

Numerical Computation of Higher-Order Derivatives

For numerical exploration of higher-order derivatives, MATLAB's finite difference methods can be applied. The choice of finite difference method (forward, backward, or central) depends on the specific requirements of the problem.

Partial Derivatives

Partial derivatives come into play when dealing with functions of multiple variables. They provide information about how the function changes concerning each input variable independently. MATLAB seamlessly handles partial derivatives through the Symbolic Math Toolbox.

Optimization and Root Finding

Derivatives play a pivotal role in optimization and root-finding algorithms, aiding in the efficient discovery of extrema and roots. MATLAB's Optimization Toolbox provides specialized functions that leverage derivative information for enhanced performance.

Minimization Example

Consider a simple minimization problem using MATLAB's fminunc function, which requires the gradient (first derivative) information for optimization.

Root Finding Example

Root finding, exemplified by MATLAB's zero function, is often employed to locate points where a function equals zero. Derivative information enhances the efficiency of the root-finding process.

Visualization of Optimization

Visualization is crucial for understanding the optimization process. MATLAB's plotting capabilities can be harnessed to depict the function and the optimization path.

Example:

Output: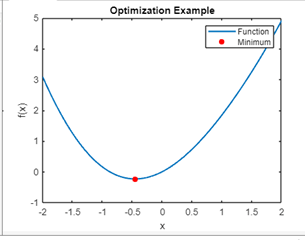

In this example, the optimization path for finding the minimum is visualized along with the function.

Harnessing Advanced Derivative Techniques with MATLAB

MATLAB's prowess in handling advanced derivative techniques empowers users to explore the intricacies of higher-order derivatives, partial derivatives, and their applications in optimization and root finding.

• The seamless integration of symbolic and numerical approaches, coupled with specialized toolboxes, makes MATLAB a formidable platform for tackling complex mathematical models and optimizing real-world systems.
• As you delve into these advanced techniques, MATLAB becomes not just a tool for computation but a catalyst for innovation and precision in mathematical modeling and analysis.
• Derivatives are fundamental in various fields, and MATLAB provides a robust platform for employing advanced techniques for their computation. In symbolic differentiation, MATLAB's Symbolic Math Toolbox allows the manipulation and analysis of mathematical expressions directly.
• This ensures precision and fidelity in obtaining derivatives without relying on numerical approximations.

Bridging the continuity: For bridging the continuity of mathematical concepts with discrete computing reality, MATLAB's numerical differentiation methods, such as finite differences, shine. These methods are particularly valuable when working with real-world data, enabling accurate derivative computations even in the presence of noise.

Handling noisy: Handling noisy data is a common challenge, and MATLAB provides advanced techniques like smoothing and curve fitting.

• Smoothing methods help reduce noise impact, while curve fitting allows modeling the underlying trend in noisy data for more accurate derivative computations.

Robust derivative: Robust derivative computation is achieved using MATLAB's numerical differentiation methods. Visualization is a key aspect of the evaluation process, and MATLAB's plotting functions facilitate clear representations, aiding in a comprehensive analysis of the data processing pipeline.

MATLAB seamlessly integrates symbolic and numerical approaches, empowering users to navigate the complexities of mathematical expressions and real-world data. Whether in research, engineering, or finance, MATLAB's capabilities ensure precise and versatile derivative computations.