Gauss and Gauss-Jordan EliminationThere are two methods of solving systems of linear equations are:
They are both based on the observation that systems of equations are equivalent if they have the same solution set and performing simple operations on the rows of a matrix, known as the Elementary Row Operations or (EROs). There are 3 EROs:
Example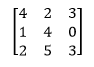
An example of interchanging rows would be r1⟵⟶r3. 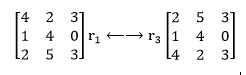
Now, starting with this matrix, an example of scaling would be: 2r2⟶r2,which describes all items in row 2 are multiplied by 2. 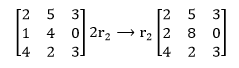
Now, starting with this matrix, an example of a replacement would be: r3-2r2⟶r3.Element-by-element, row 3, is replaced by the element in row 3 minus 2 * the corresponding items in row 2. These yields: 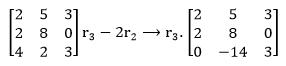
Both the Gauss and Gauss-Jordan methods begin with the matrix form Ax = b of a system of equations, and then augment the coefficient matrix A with the column vector b. Gauss EliminationThe Gauss Elimination method is a method for solving the matrix equation Ax=b for x. The process is:
ExampleUse a 2 x 2 system, the augmented matrix would be: 
Then, EROs are used to get the augmented matrix into an upper triangular form: 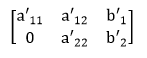
So, it is simply to replace a21 with 0. Here, the primes indicate that the values have been change. Putting this back into the equation form yield 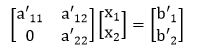
Executing this matrix multiplication for each row results in: 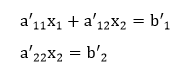
So, the solution is: 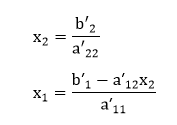
Similarly, for the 3x3 system, the augmented matrix is reduced to an upper triangular form: 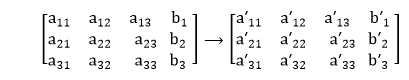
This will be done orderly by first getting a0in the a21 position, then a31, and finally a32. Then, the solution will be: 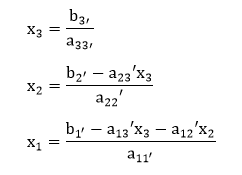
Consider the following 2x2 system of equations: x1+2x2=2 As the matrix equation Ax = b, this is: 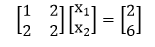
The first process is to augment the coefficient matrix A with b to get an augmented matrix [A| b]: 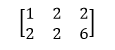
For the forward elimination, we need to get a0 in the a21 position. To accomplish this, we can change the second line in the matrix by subtracting from it 2 * the first row. The way we would write this ERO is: 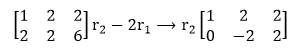
Now, putting it back in the matrix equation form: 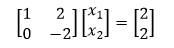
says that the second equation is now -2x2= 2 so x2 = -1. Plugging into the first equation: x1+2(-1)=2 This is called a back-substitution. Gauss-Jordan EliminationThe Gauss-Jordan Elimination method start the similar technique that the Gauss Elimination method does, but then the instead of back-substitution, the elimination continues. The Gauss-Jordan method consists of:
ExampleUse 2x 2 system, the augmented matrix would be: 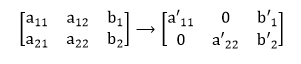
Use 3x 3 system, the augmented matrix would be: 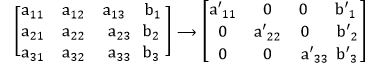
Note: The resulting diagonal form does not include the right-most column.For example, for the 2x2 system, forward elimination yielded the matrix: 
Now, to continue with back elimination, we want a0in the a12position. 
So, the solution is 
Here is an example of a 3x3 system: 
In matrix form, the augmented matrix [A|b] is 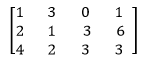
Forward substitution (done orderly by first getting a0in the a21position, then a31 , and finally a32): 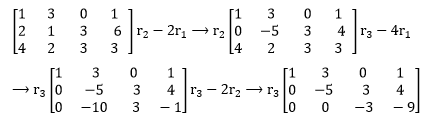
For the Gauss technique, this is followed by back-substitution: 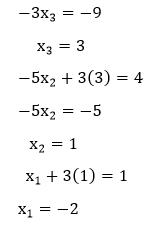
For the Gauss-Jordan technique, this is instead followed by back elimination: 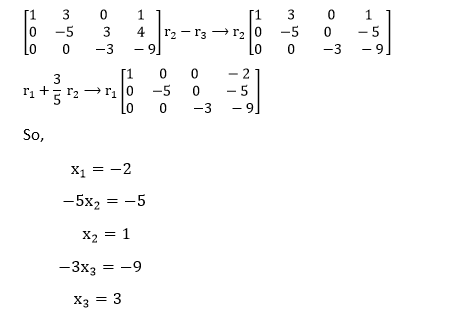
Here's an example of operating these substitutions using MATLAB:
Next TopicMATLAB rref
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









