Matlab diff

Introduction

The diff function in MATLAB is used for numerical differentiation, which involves calculating the differences between consecutive elements of a vector. This function is particularly useful for estimating derivatives of discrete data or signals.

Understanding the Basics

The diff function in MATLAB is designed to compute the differences between consecutive elements of an array.

Its basic syntax is simple:

Here, A is the input array, and B is the output array containing the differences between consecutive elements of A. By default, the differences are computed along the first non-singleton dimension of A. The result, B, is one element shorter than A along this dimension.

Simple Usage Examples

Let's start with some basic examples to illustrate the fundamental usage of the diff function.

In this example, the array A represents the sequence of perfect squares, and B will be the differences between consecutive elements.

Output:

Each element in B is computed as the difference between the corresponding element in A and the one preceding it.

Applications in Numerical Analysis

The diff function is particularly useful in numerical analysis, where it finds applications in various mathematical and scientific domains. Let's explore some common use cases.

Differentiation

One of the primary applications of the diff function is numerical differentiation. Given a set of discrete data points, the differences between consecutive elements can approximate the derivative of the underlying function.

Example: Numerical differentiation

In this example, we generate a set of points representing the sine function and then use diff to compute the numerical derivative. The result is plotted alongside the original function.

Output: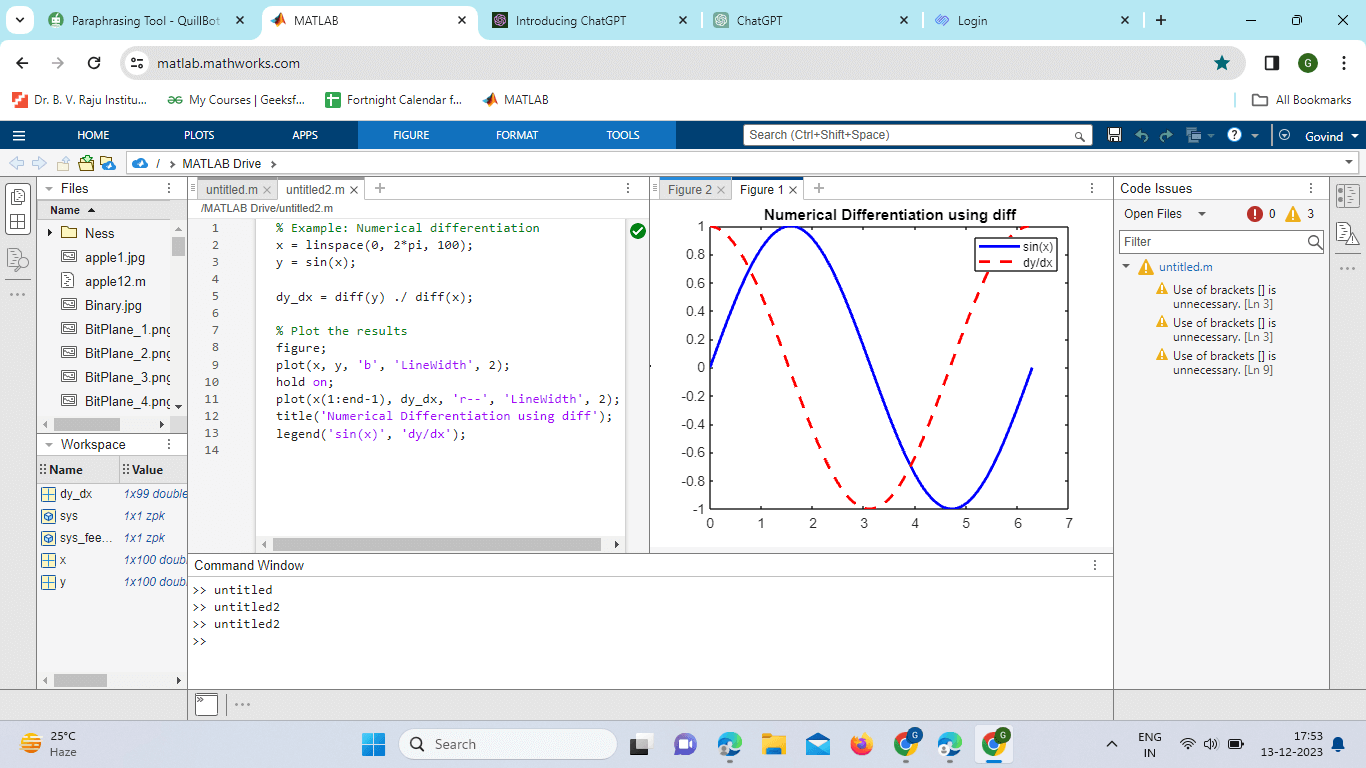

Explanation:

It shows how to numerically approximate a function's derivative visually using the diff function. The results are plotted for comparison. The red dashed curve represents the numerical derivative of the sine function with respect to x, while the blue curve represents the sine function.

Signal Processing

The diff function is also employed in signal processing for tasks such as edge detection and feature extraction. By computing the differences between consecutive elements of a signal, one can identify abrupt changes or peaks.

Example: Edge detection using diff

Output: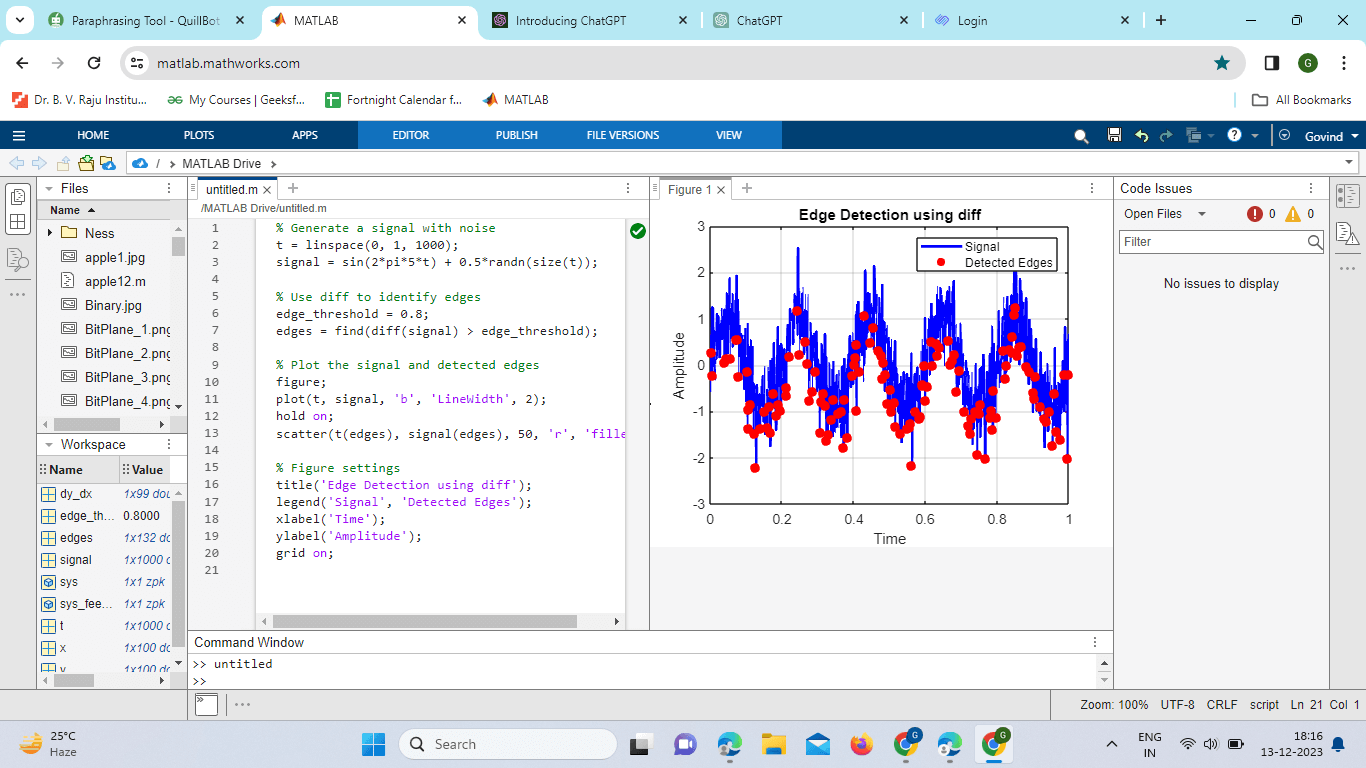

Explanation:

Added Labels and Grid: added x-axis and y-axis labels for Clarity and turned on the grid for better visualization.

Defined Edge Threshold: introduced a variable edge_threshold to make it easier to adjust the threshold for edge detection.

Comments for Clarity: Add comments to explain the purpose of each section of the code. Modify the edge_threshold variable to fine-tune the sensitivity of edge detection based on your specific requirements.

Advanced Features of the Different Functions

Specify Dimension:

The diff function allows you to specify the dimension along which differences are calculated. This is particularly useful when working with multidimensional arrays or matrices. By default, diff operates along the first non-singleton dimension.

Higher Order Differences:

In addition to first-order differences, the diff function can compute higher-order differences. By specifying the order as the second argument, you can calculate second-order, third-order, and so on differences. This flexibility is valuable in scenarios where higher-order derivatives are required.

Handling NaN Values:

The diff function gracefully handles datasets containing NaN (Not a Number) values. It preserves NaN values in the output, ensuring that differences involving NaN elements result in NaN. This feature is essential for scenarios where missing or undefined data points are present.

Custom Differences:

For specialized differencing schemes, the diff function allows users to specify custom differences using the second input argument. This capability provides a high degree of flexibility in tailoring the differencing operation to specific requirements.

Differentiation with Respect to Specific Elements:

With the ability to differentiate with respect to specific elements in the array, the diff function becomes even more versatile. This feature is particularly useful when the goal is to analyze how individual elements contribute to the overall change in the dataset.

Vectorized Input:

The diff function supports vectorized input, enabling the differencing operation to be performed on multiple vectors simultaneously. This capability enhances efficiency and convenience when working with large datasets or when differencing multiple variables.

Performance Considerations:

When dealing with large datasets, specifying the data type of the input can significantly improve the performance of the diff function. By choosing an appropriate data type, such as 'single' precision, users can optimize the computation for efficiency.

• These advanced features collectively empower users to tailor the behavior of the different functions to meet specific demands in various numerical differentiation scenarios.
• Whether dealing with multidimensional data, custom differencing schemes, or performance optimization, the diff function provides a versatile toolset for diverse applications.

This explored the different functions in MATLAB, uncovering its basic usage, applications in numerical analysis and signal processing, and advanced features.

• MATLAB's diff function proves to be a valuable tool for a wide range of tasks, from simple array manipulation to complex mathematical computations.
• As you continue your MATLAB journey, consider experimenting with the different functions in different contexts, exploring its capabilities, and fine-tuning its parameters to suit your specific needs.
• Whether you're analyzing data, performing numerical simulations, or working on signal processing tasks, the diff function will likely become an indispensable part of your MATLAB toolkit.