MATLAB limit

Introduction:

A fundamental idea in mathematical analysis is how functions behave when variables get closer to certain values. Understanding this behavior, particularly in the context of calculus and mathematical analysis, depends heavily on the concept of limits. The limit function, a crucial tool provided by the well-known computer program MATLAB, allows users to determine function limits symbolically.

Comprehending the Idea of Limitations

When understanding how functions act close to specific points or as variables get closer to specific values, limits are crucial. They are essential in many mathematical fields, including calculus, differential equations, and real analysis, and they aid in determining the behavior of functions around critical points. Mathematicians and scientists can learn more about how functions behave in various scenarios by evaluating limits, which lays a strong basis for more mathematical research and problem-solving.

Importance of the limit in MATLAB Operation

• The limit function in MATLAB is a potent computational tool that makes it easier to compute limits symbolically. MATLAB allows users to evaluate complex limits, derivatives, integrals, and other mathematical operations by utilizing the Symbolic Math Toolbox's capabilities to manipulate mathematical expressions symbolically.
• This function is invaluable in both academic and practical settings, enabling researchers, engineers, and students to conduct sophisticated analyses and explore complex mathematical topics effectively.

Syntax:

The syntax for the limit function in MATLAB is as follows:

The parameters are as follows:

f: The expression or function for which the limit needs to be calculated.

x: The variable that the limit is calculated about.

a: The value at which variable x is getting close.

The formula f's limit as x gets closer to the value an is shown by the output L.

Symbolic Math Toolbox in MATLAB includes the limit function:

In calculus and mathematical analysis, the idea of limits is essential because it sheds light on how functions behave close to particular points or as variables get closer to particular values.

The Symbolic Math Toolbox in MATLAB includes the limit function, which enables users to handle and work with mathematical statements symbolically as opposed to quantitatively. MATLAB allows users to carry out intricate mathematical operations, such as the evaluation of limits, derivatives, integrals, and more, using symbolic expression by utilizing symbolic computations.

Example:

Output: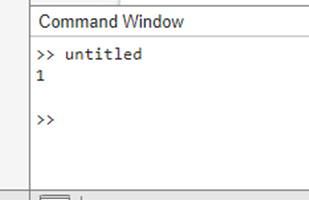

The syms x command in this code sample makes it possible to consider the variable x as a symbolic variable, allowing the usage of symbolic expressions and operations. Calculus limit evaluation is sometimes illustrated with the function f, which is defined as the sine of x divided by x. Next, when x gets closer to zero, the limit function determines the function's limit. The disp function then displays the computed limit.

• To work with symbolic expressions and calculations in MATLAB, one must have the Symbolic Math Toolbox. It provides several tools and functions for symbolic mathematics, allowing users to carry out a variety of mathematical operations and analyses that would be difficult or time-consuming to carry out by hand.

limit of Symbolic Vector Expressions

Using the limit function from the Symbolic Math Toolbox, you may use MATLAB to find the limit of expressions in symbolic vectors. When working with expressions involving symbolic vectors, you must take into account the particular components of the vectors used to calculate the limit. As long as you indicate the direction of the limit along the elements of the vector, the limit function can handle these situations.

Example:

Output: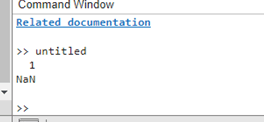

Explanation:

This line declares the symbolic variables x and y.

f1 = sin(x)/x; - The variable f1 denotes the symbolic vector expression's first element, sin(x)/x.

f2 = cos(y)/y; - The second component of the symbolic vector expression, cos(y)/y, is represented by the variable f2.

L1 = limit(f1, x, 0); - As x gets closer to 0, this line calculates the limit of the first element, f1.

L2 = limit(f2, y, 0); - As y gets closer to 0, this line calculates the limit of the second element, f2.

L = [L1; L2]; - In this case, we build the final vector L, which has the calculated limits of each element.

Disp (L); - This line shows the calculated limits as a vector.