MATLAB Quadprog

Introduction

MATLAB, a widely used numerical computing environment, offers a powerful optimization toolbox that includes various functions for solving optimization problems. One such function is quadprog, which stands for quadratic programming. Quadratic programming is a special case of mathematical optimization where the objective function is quadratic, and the constraints are linear. In this comprehensive guide, we will delve into the details of quadprog in MATLAB, exploring its syntax and applications and providing practical examples to enhance your understanding.

Understanding Quadratic Programming

Basics of Quadratic Programming

Quadratic programming involves optimizing a quadratic objective function subject to linear equality and inequality constraints. The general form of a quadratic programming problem can be expressed as follows:

minimize12minimize21 xTHx+fTx subject to subject toA⋅x≤b C⋅x=d

Here, x is the vector of decision variables, H is a symmetric positive definite matrix, f is a column vector, and A, b, C, and d represent matrices and vectors defining the linear constraints.

The quadprog Function

The quadprog function in MATLAB is designed to solve quadratic programming problems.

Its syntax is as follows:

Let's break down the parameters:

• H is the Hessian matrix of the quadratic objective function.
• f is the linear term vector of the objective function.
• A and b are matrices defining the linear inequality constraints (an⋅x≤b).
• Aeq and beq are matrices defining the linear equality constraints (Aeq⋅x=beq).
• lb and ub are vectors defining the lower and upper bounds of the decision variables.
• x0 is the initial guess for the solution.

Options is a structure specifying various options for the optimization.

The function returns the optimal solution vector x, the minimum value of the objective function value, an exit flag indicating the status of the optimization, additional output information output, and the Lagrange multipliers lambda associated with the constraints.

Practical Examples

To better understand how to use the quadprog function, let's walk through a couple of practical examples.

Portfolio Optimization

Consider a financial portfolio optimization problem where you want to allocate funds to different assets to maximize the expected return while maintaining a certain level of risk.

The objective function can be formulated as:

maximize2ΣmaximizeμTx-2γ xTΣx

Here, μ is the vector of expected returns, ΣΣ is the covariance matrix of returns, x is the vector of asset weights, and γ is the risk aversion parameter.

In this example, we maximize the expected return while constraining the sum of weights to be equal to 1. The quadprog function helps us find the optimal asset weights.

Output: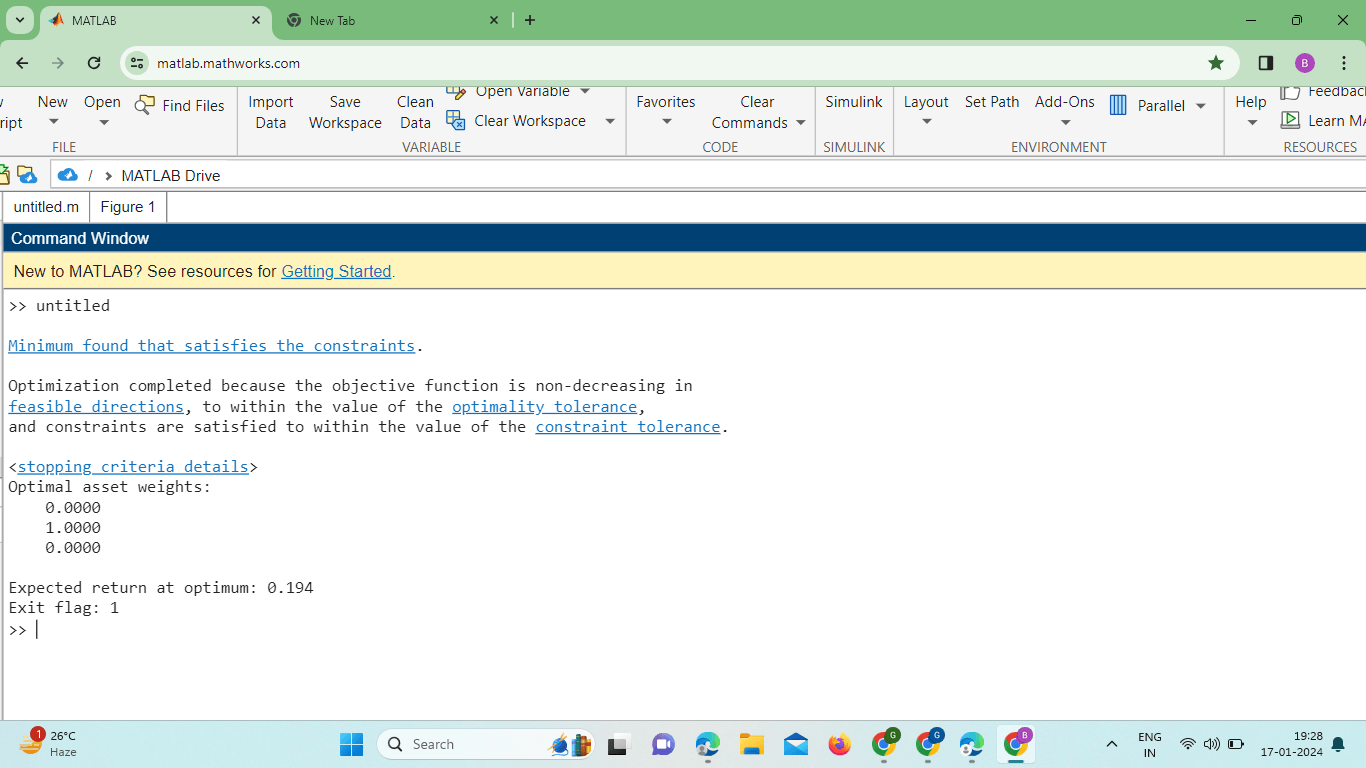

Define the Parameters:

Here, we have a financial scenario with three assets. mu represents the expected returns for each asset, and Sigma is the covariance matrix that captures the relationships between the assets. Gamma is the risk aversion parameter.

Formulate the Quadratic Programming Problem:

The Hessian matrix H is formed by multiplying the risk aversion parameter gamma with the covariance matrix Sigma.

The linear term vector f is the negative of the expected returns (-mu).

The linear equality constraint is specified using Aeq and beq. In this case, it ensures that the sum of the asset weights is equal to 1.

Solve the Problem Using Quadprog:

The quadprog function is used to solve the quadratic programming problem.

H and f define the objective function, and Aeq and beq define the linear equality constraint.

The decision variable x represents the optimal asset weights, the value is the minimum value of the objective function, the exit flag indicates the optimization status, the output provides additional output information, and lambda contains the Lagrange multipliers associated with the constraints.

Display the Results:

The optimal asset weights, expected return at the optimum, and exit flag are displayed in the console.

Example: Support Vector Machines (SVM)

Quadratic programming is commonly used in machine learning, particularly in the training of support vector machines (SVMs). Let's consider a simplified linear SVM problem:

Minimize12 minimize21 wTw subject to subject toyi (wTxi +b)≥1

Here, w is the weight vector, b is the bias term, xi is a training sample, and is its corresponding class label.

Output:

In this example, we use synthetic data to train a linear SVM. The quadprog function helps us find the optimal weight vector and bias term, allowing the SVM to classify new data points.

Choosing the Right Algorithm:

quadprog uses an interior-point algorithm by default, but for large-scale problems, consider using specialized algorithms like active-set or trust-region-reflective by specifying the 'Algorithm' option.

Regularization:

Ensure that the Hessian matrix (H) is positive definite to guarantee a unique solution.

For ill-conditioned problems, consider adding a small regularization term to H to improve numerical stability.

Scaling:

Scaling the decision variables and constraints can significantly impact the performance of the optimization. Use the 'ScaleProblem' option to scale the problem based on its characteristics automatically.

Warm Starts:

Providing a good initial guess (0x0) can speed up convergence. Use the solution of a similar problem or a heuristic method to obtain a reasonable starting point.

Output Interpretation:

Pay attention to the exit flag, which indicates the status of the optimization. A positive value (typically 1) usually indicates success.

• MATLAB's quadprog function is a valuable tool for solving quadratic programming problems, offering a flexible and efficient optimization framework.
• Whether you're working on financial portfolio optimization, machine learning, or any other application involving quadratic objectives and linear constraints, quadprog provides a robust solution.
• By understanding its syntax, applications, and best practices, you can leverage this powerful tool to tackle a wide range of optimization challenges in your numerical computing endeavors.

Sensitivity Analysis:

Perform sensitivity analysis to understand how changes in problem parameters impact the solution. This can be achieved by varying the coefficients in the objective function or adjusting constraint bounds.

Constraint Violations:

Inspect the Lagrange multipliers to identify which constraints are active or violated. Positive multipliers indicate active constraints, while negative ones suggest violated constraints.

• Understanding and effectively utilizing the quadprog function in MATLAB opens up a realm of possibilities for solving complex quadratic programming problems.
• By extending your knowledge through practical examples, exploring additional details, and incorporating tips and best practices, you can confidently apply quadprog to diverse scenarios, ranging from finance to machine learning.

As you master its capabilities, MATLAB's quadprog becomes an invaluable tool in your optimization toolkit, providing robust solutions to a myriad of real-world challenges.

Example:

Output:

Explanation:

Project Parameters:

resources required: Vector representing the resources required for each project.

profitPerProject: Vector representing the profit generated by each project.

Budget and Resource Constraints:

budget constraint: Maximum budget available.

resource constraint: Maximum total resources available.

Quadratic Programming Formulation:

The Hessian matrix H is constructed to maximize profit (equivalent to minimizing negative profit).

The linear term vector f is set to zeros.

Equality constraints (Aeq and be) are defined based on resource requirements.

Binary decision variables (lb and ub) are used to indicate project selection (1 for selected, 0 for not selected).

Solving the Resource Allocation Problem:

The quadprog function is employed to find the optimal solution that maximizes total profit while adhering to constraints.

Displaying Results:

The optimal project selection, total profit at the optimum, exit flag, and Lagrange multipliers associated with equality constraints are displayed.

This example demonstrates how quadratic programming can be applied to solve resource allocation problems, where decision variables are binary and subject to linear equality constraints. The quadprog function aids in efficiently optimizing such problems, making it a versatile tool for a wide range of applications.