Permute in MATLABIntroductionIn MATLAB, the permute command is a powerful tool used for rearranging elements within a multidimensional array. This function enables users to manipulate the order of dimensions in an array, offering flexibility in data organization. By specifying the desired order of dimensions, users can reshape their data efficiently. In addition to permute, MATLAB also provides the permute function for reversing the permutation process. Basic SyntaxThe basic syntax for the permute function is as follows: B = permute(A, order) A: The input multidimensional array. Order: A vector specifying the order of dimensions in the output array. Key FeaturesDimension Manipulation: The primary purpose of permute is to manipulate the dimensions of a multidimensional array. This is particularly useful when dealing with data organized in a way that doesn't align with the desired analysis. Size Adjustment: permute allows users to change the size of the array along different dimensions. This is crucial when preparing data for specific operations or algorithms. Circular Shift (circshift): The circshift function is often combined with permute to achieve circular shifts within the array. This is useful for creating sliding window operations or cyclic data transformations. Reshaping (reshape): While permute focuses on rearranging dimensions, the reshape function in MATLAB is used to alter the shape of an array. These two functions are often used in conjunction for comprehensive data manipulation. Transpose Relationships: Understanding the relationship between permute and transpose operations (' and .') is essential. The output of permuting a matrix is equivalent to the transpose (.') of the output of the permute with inverted dimensions. This relationship simplifies the understanding of how data transforms through Permutation. Reverse Permutation (permute): The permute function in MATLAB serves as the inverse operation to permute. It allows users to reverse the order of dimensions, restoring the original structure of the array. ImplementationLet's consider a practical example where permute is applied to a 3D array: Output: 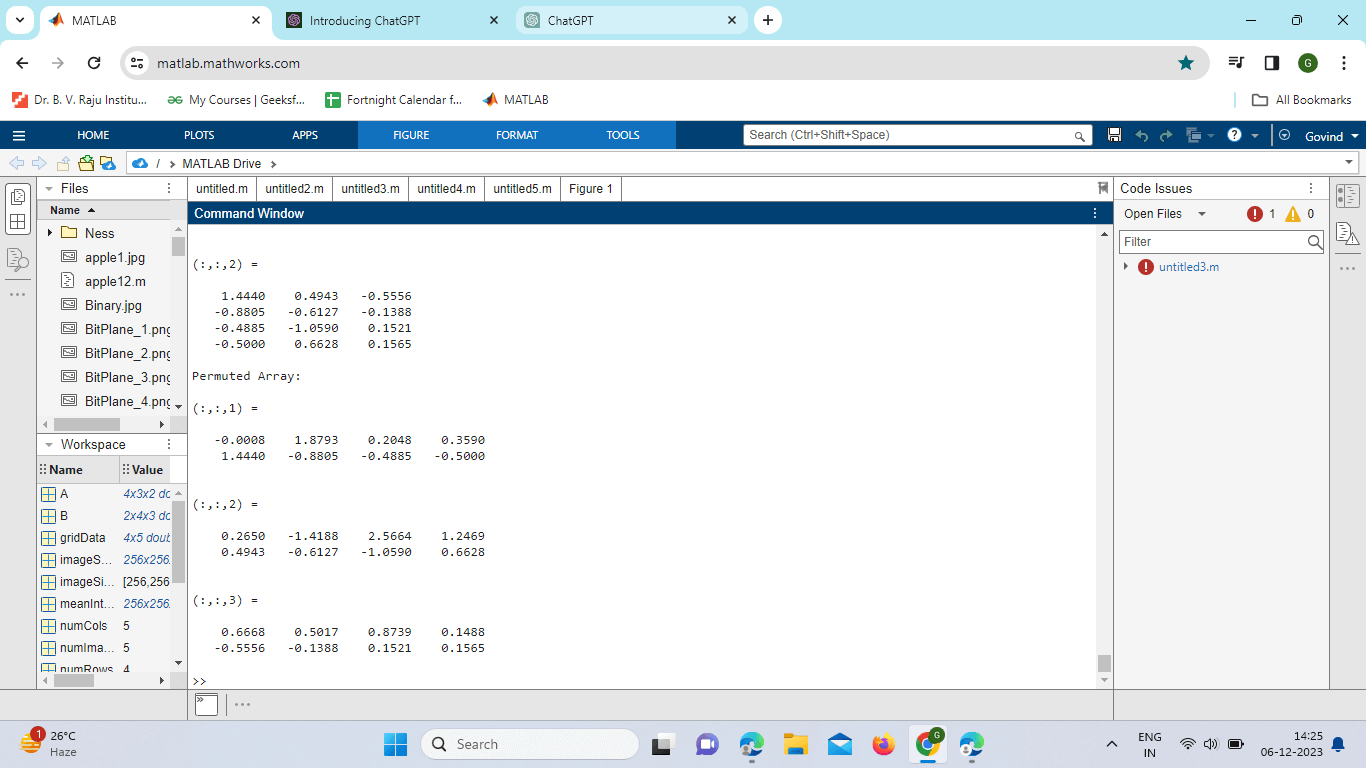
Explanation: In this example, the dimensions of the original array A are rearranged as specified in the permute command. The permute function in MATLAB provides a versatile solution for rearranging dimensions within multidimensional arrays. Whether adjusting data for specific analyses, creating circular shifts, or preparing input for algorithms, permute is a valuable tool for data manipulation. Understanding its relationship with transpose operations and the availability of the permute function further enhances its utility in MATLAB programming. Advanced Usage of permute in MATLABDimensional Shuffling for Analysis One of the primary applications of the permute function is in preparing data for analysis. Consider a scenario where data is organized in a way that doesn't align with the requirements of a particular algorithm or statistical analysis. Permute can be employed to efficiently shuffle dimensions, bringing the data into a format conducive to the analysis at hand. Size Adjustment and Integration with ReshapeIn addition to rearranging dimensions, permute is useful for adjusting the size of an array along different dimensions. This is particularly valuable when preparing data for operations that require specific input sizes. % Example: Adjusting size using permute and reshape originalData = randn(2, 3, 4); % 3D array permutedData = permute(originalData, [3, 1, 2]); % Shuffling dimensions reshapedData = reshape(permuted data, [4, 2, 3]); % Reshaping % Now, 'reshapedData' has a different size and dimension order. Circular Shifts with circshift: Combining the circshift function with permute allows for circular shifts within an array. This is particularly useful in scenarios where cyclic patterns or sliding window operations are required. Relationship with Transpose Operations: Understanding the relationship between permute and transpose operations (' and .') is crucial for effectively utilizing these functions. The transpose of the permuted array is equivalent to the permute operation with the inverse order of dimensions. Reverse Permutation with permute: The permute function serves as the inverse of permute and is used to reverse the order of dimensions, effectively restoring the original structure of the array.
Example: Output: 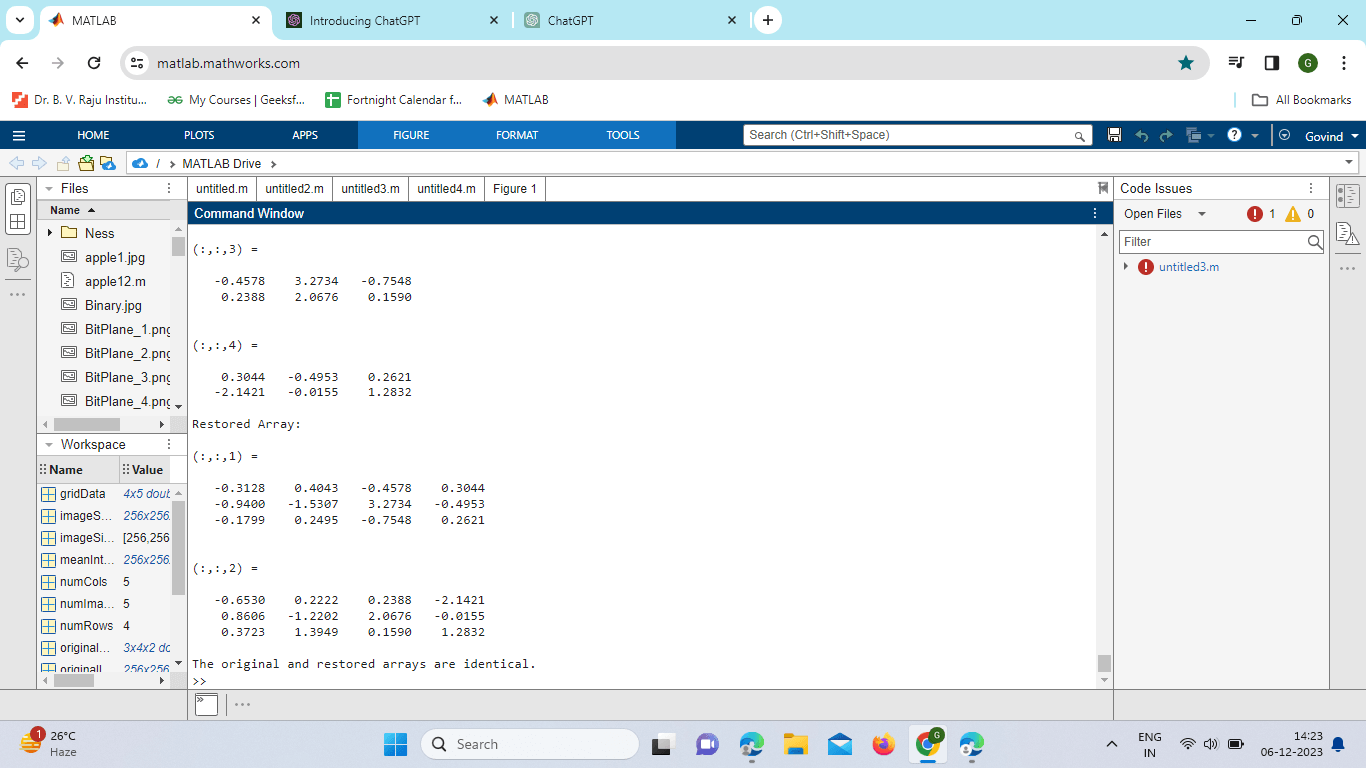
Explanation: Creates a random 3D array (originalArray). Uses permute to rearrange the dimensions of the array (permutedArray). Uses permute to restore the original order of dimensions (restoredArray). Check if the original and restored arrays are identical. ExampleOutput: 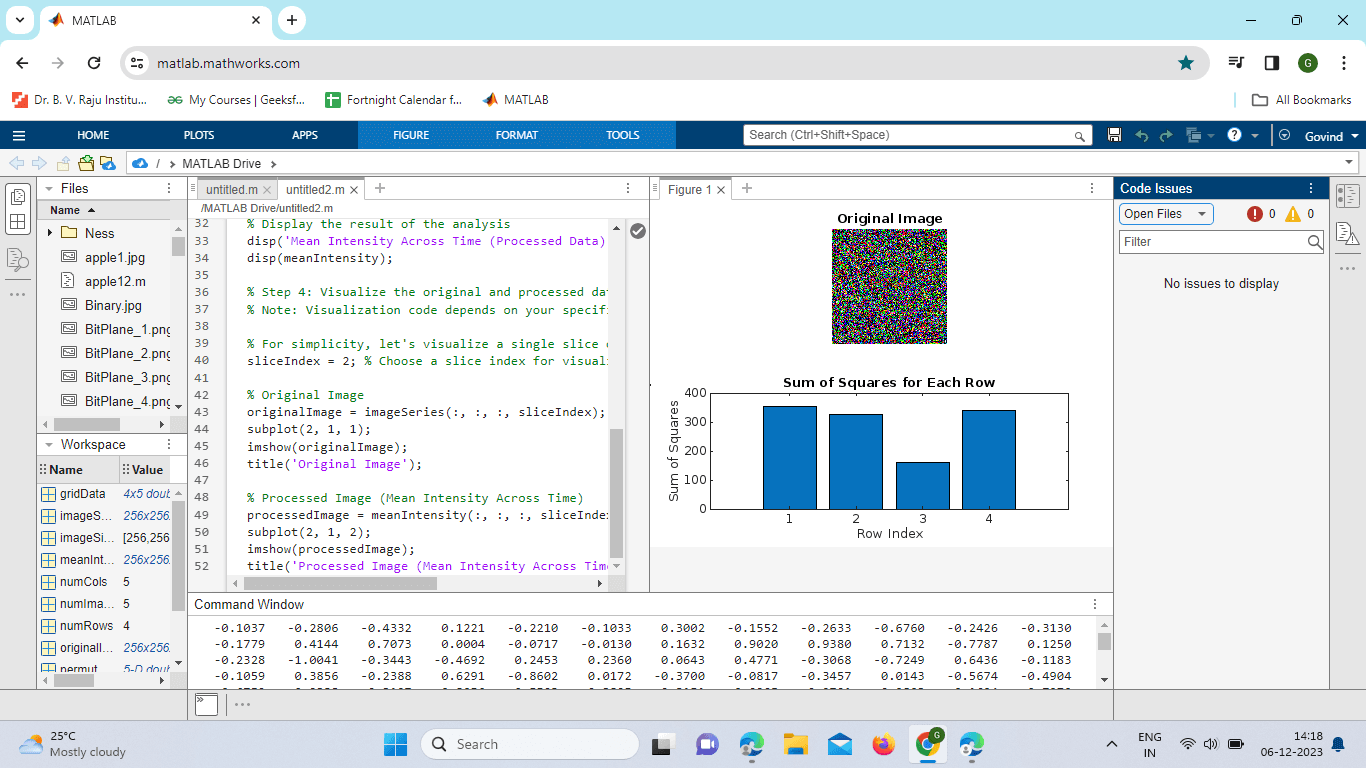
Explanation: Creating 4D Array: We create a 4D array (imageSeries) representing a series of 3D images over time. Using permute: We use the permute function to rearrange dimensions, placing the time dimension (4th dimension) at the end for better analysis. Analysis: We perform a simple analysis of the permuted data. In this example, we compute the mean intensity across time for each pixel. Visualization: We visualize a single slice of one image before and after processing for comparison. Example: Output: 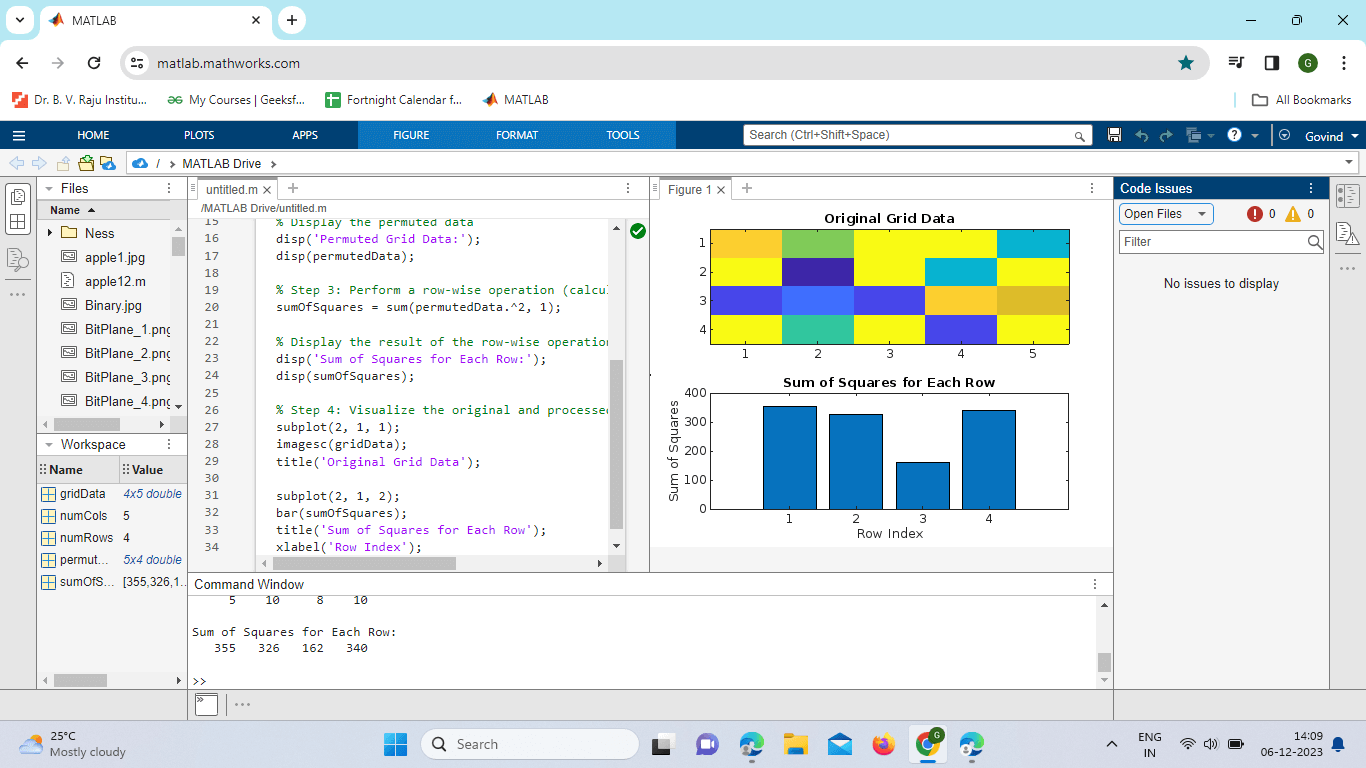
Explanation: Creating 2D Grid: We create a random 2D grid (gridData) representing some data with rows and columns. Using permute: We use the permute function to transpose the dimensions, effectively treating columns as rows and vice versa. Row-wise Operation: We perform a row-wise operation, calculating the sum of squares for each row using the permuted data. Visualization: For illustration purposes, we visualize the original grid data and the result of the row-wise operation.
Next TopicHeaviside in Matlab
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









