Linear AlgebraSolving a Linear SystemA linear algebraic equation is an equation of the system a1 x1+a2 x2+a3 x3+⋯+an xn=b where a's are constant coefficients, the x's are the unknowns, and b is a constant. A solution is a sequence of numbers s1,s2, and s3that satisfies the equation. Example 4x1+5x2-2x3=16 is such an equation in which there are three unknown: x1,x2,andx3. One solution to this equation is x1=3,x2=4 and x3=8,since 4*3+5*4-2*8 is equal to 16. A system of a linear algebraic equation is a set of the equation of the form: a11 x1+a12 x2+a13 x3+⋯+a1n xn=b1 This is called an m*n system of equations; there are m equations and n unknowns. Matrix FormsBecause of the method that matrix multiplication works, these equations can be defined in the matrix form as Ax = b where A is the matrix of the coefficients, x is the column vector of the unknown, and b is a column vector of the constant from the right-hand side of the equations: A x = b A solution set is a set of all possible solutions to the system of equation (all sets of value for the unknowns that solve the equation). All systems of linear equations have either:
Solution using matrix InverseProbably the simple way of solving this system of equations is to use the matrix inverse. A-1 A=1 We can multiply both sides of the matrix equation AX= B by A-1to get A-1 AX=A-1 B Or X=A-1 B So, the solution can be found as a product of the inverse of A and the column vector b. In MATLAB, there are two method of doing this, using the built-in inv function and matrix multiplication, and also using the "\" operator: Solving 2x2 Systems of EquationsThe simplest system is a 2 x 2 system, with just two equations and two unknowns. For these systems, there is a simple definition for the inverse of a matrix, which uses the determinant D of the matrix. For a coefficient matrix, A generally defined as 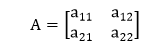
the determinant D is defined as a11 a22-a12 a21 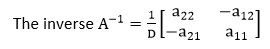
Example x1+3x2=-2 This would be written in matrix form as 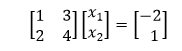
The determinant D = 1*4 -3*2 = -2. 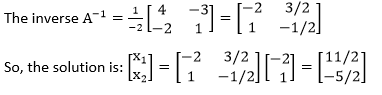
MATLAB has built-in functions det to find the determinant of the matrix.
Next TopicGauss and Gauss-Jordan Elimination
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









