Matlab randn

Introduction:

MATLAB, a powerful programming language, and environment designed for numerical computing, provides a wide array of functions to manipulate and generate random numbers. One such function is randn, a cornerstone in statistical analysis, Monte Carlo simulations, and various other applications. In this comprehensive guide, we will delve into the intricacies of the randn function, exploring its features, applications, and best practices.

Basics of randn

At its core, the randn function in MATLAB generates random numbers from a standard normal distribution with a mean of 0 and a standard deviation of 1. This distribution, also known as the Gaussian or normal distribution, is a fundamental concept in statistics and probability theory.

The basic syntax of randn:

Here, size denotes the dimensions of the output array, determining the number of random numbers generated. The result is an array filled with random values conforming to the standard normal distribution.

Applications in Statistical Analysis:

Hypothesis Testing: The randn function is frequently employed in hypothesis testing scenarios. Researchers use it to simulate data under the null hypothesis, allowing them to assess the likelihood of obtaining observed results purely by chance.

% Simulating data for hypothesis testing

null_hypothesis_data = randn(1, 1000);

Monte Carlo Simulations: Monte Carlo simulations involve using random sampling to obtain numerical results for various mathematical problems. The randn function is indispensable in generating random inputs for these simulations.

Custom Mean and Standard Deviation: While randn generates random numbers with a mean of 0 and a standard deviation of 1 by default, users can customize these parameters to fit specific requirements.

% Custom mean and standard deviation
custom_mean = 5;
custom_std_dev = 2;
custom_data = custom_mean + custom_std_dev * randn(1, 1000);

Multidimensional Arrays: The randn function can generate random numbers for multidimensional arrays, providing a convenient tool for simulating complex scenarios.

% Multidimensional array example
multi_dim_data = randn(3, 4, 5); % 3x4x5 array of random numbers

Reproducibility with Seed: To ensure reproducibility in simulations or analyses, MATLAB allows users to set a seed for the random number generator. This ensures that the same sequence of random numbers is generated each time the code is run.

% Setting seed for reproducibility
seed_value = 42;
rng(seed_value);
reproducible_data = randn(1, 100);

Best Practices and Tips:

Vectorization: MATLAB's strength lies in its ability to perform operations on entire arrays at once. Vectorization, or the use of array operations, enhances the efficiency of code utilizing the randn function.

% Vectorized example
vectorized_data = custom_mean + custom_std_dev * randn(1, 1000);

Preallocating Arrays: Preallocating arrays before using the randn function can significantly improve performance, especially in large-scale simulations.

% Preallocating arrays
num_samples = 10000;
result_data = zeros(1, num_samples);
for i = 1:num_samples
    result_data(i) = randn();
end

MATLAB's randn function serves as a versatile and essential tool for generating random numbers conforming to a standard normal distribution. Its applications range from statistical analysis to Monte Carlo simulations, making it a valuable asset for researchers, engineers, and data scientists alike. By understanding its features, customizing parameters, and adhering to best practices, users can harness the full power of the randn function in MATLAB for a myriad of numerical computing tasks.

Generating Correlated Random Variables:

The randn function in MATLAB is not limited to generating independent random variables; it can also be used to generate correlated random variables. This is particularly useful in scenarios where the relationship between variables needs to be simulated realistically.

% Generating correlated random variables
correlation_matrix = [1 0.8; 0.8 1];
correlated_data = chol(correlation_matrix) * randn(2, 1000);

In this example, chol is used to compute the Cholesky decomposition of the correlation matrix, and the result is multiplied by randn to generate correlated data. This technique is valuable in financial modeling, risk analysis, and various scientific simulations.

Random Number Generation for Random Processes:

Random processes are common in fields like signal processing and communication systems. MATLAB's randn function proves indispensable in simulating these processes, aiding in the analysis and design of systems.

% Simulating random process
num_samples = 1000;
time = 1:num_samples;
random_process = cumsum(randn(1, num_samples));

In this example, cumsum is used to obtain a cumulative sum of the random numbers, creating a simple random walk. Such simulations are fundamental in understanding system behaviors over time.

Generating Random Matrices and Images:

The randn function is not confined to generating one-dimensional arrays; it can be extended to create random matrices and even images. This capability is valuable in testing algorithms, studying image processing techniques, and more.

% Generating a random matrix
random_matrix = randn(3, 3);

% Displaying a random image
random_image = randn(256, 256);
imshow(random_image, []);

By adjusting the dimensions, users can create random matrices of different sizes or generate images with varying resolutions. This versatility makes the randn function a valuable tool in experimental and algorithmic development.

Performance Considerations and Parallelization:

For large-scale simulations or data generation tasks, optimizing code becomes crucial. MATLAB offers various techniques to enhance performance, such as parallelization and efficient memory usage.

% Parallelized random number generation
num_simulations = 1000;
parallel_pool = carpool; % Start parallel pool
simulated_data_parallel = randn(parallel_pool, num_simulations, 1);
delete(parallel_pool); % Delete parallel pool

By utilizing the parallel computing toolbox, the randn function can be parallelized to generate random numbers concurrently, significantly reducing computation time for large-scale simulations.

Implementation:

% Exampl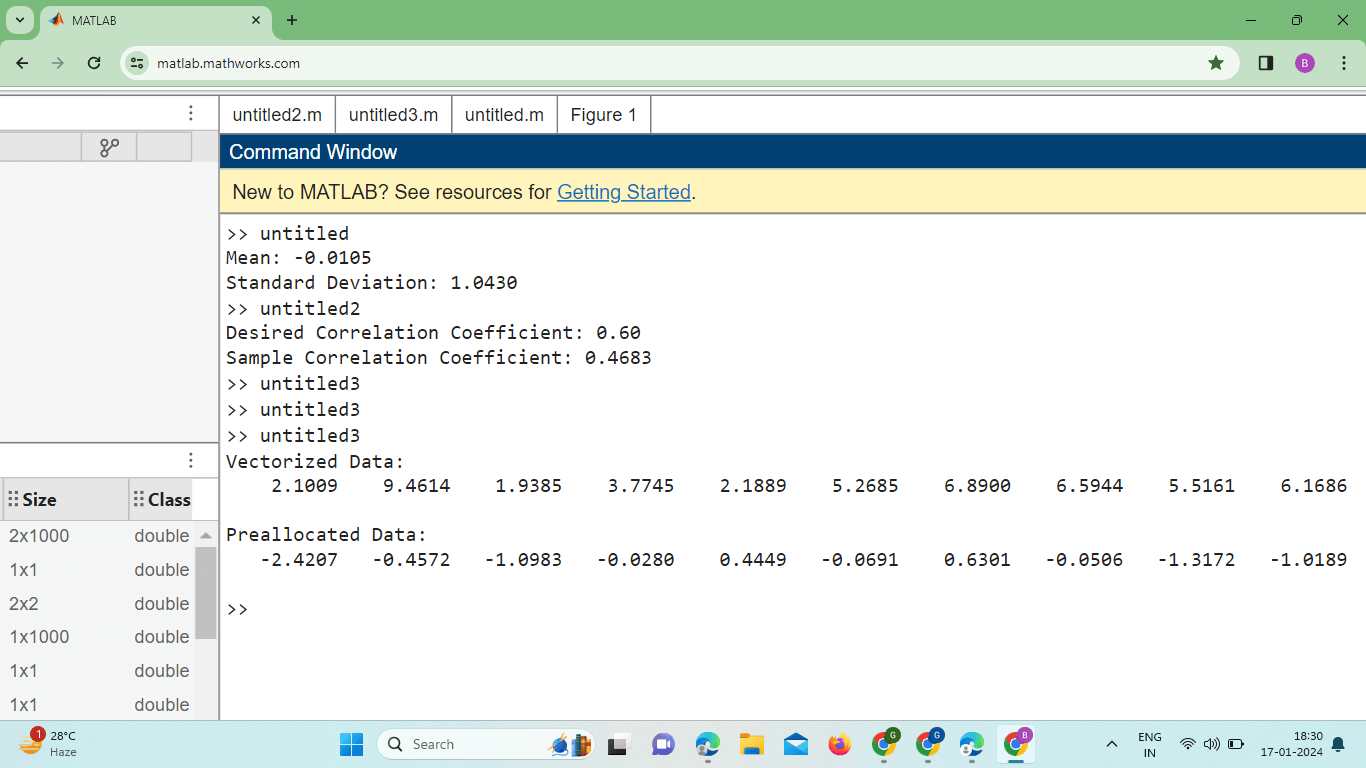e: Efficient Random Number Generation using randn
% Vectorized Example:
custom_mean = 5;
custom_std_dev = 2;

% Using vectorization to generate random data efficiently
vectorized_data = custom_mean + custom_std_dev * randn(1, 1000);

% Preallocating Arrays Example:
num_samples = 10000;

% Preallocating an array for improved performance
result_data = zeros(1, num_samples);

% Generating random numbers using a loop
for i = 1:num_samples
result_data(i) = randn();
End

% Displaying results
disp('Vectorized Data:');
disp(vectorized_data(1:10)); % Displaying first 10 elements for brevity

disp('Preallocated Data:'); 

disp(result_data(1:10)); % Displaying first 10 elements for brevity  

Output:

Explanation:

Vectorized Example: The vectorized_data is generated efficiently using vectorization, taking advantage of MATLAB's ability to perform operations on entire arrays at once. This is particularly useful when generating a large number of random numbers.

Preallocating Arrays Example: The result_data array is preallocated before using a loop to generate random numbers. Preallocating arrays can significantly improve performance, especially in large-scale simulations, by avoiding the need to resize the array during each iteration of the loop.

Displaying Results: The first 10 elements of both the vectorized and preallocated data arrays are displayed for verification.

Limitations and Caveats:

While the randn function is a powerful tool, it's essential to be aware of its limitations. The generated random numbers are based on algorithms and may not be truly random. Users should exercise caution in cryptographic applications and ensure they understand the underlying principles of random number generation.

The randn function in MATLAB is a versatile and indispensable tool for a wide range of applications.
Its ability to generate random numbers from a standard normal distribution, along with advanced features such as customization, correlation, and multidimensional array support, makes it a cornerstone in statistical analysis, simulations, and various scientific endeavors.
By mastering the intricacies of the randn function and incorporating best practices, MATLAB users can unlock its full potential in their numerical computing tasks.

Implementation:

% MATLAB Program: Understanding randn Implementation
% Step 1: Setting seed for reproducibility (optional)
seed_value = 42;
rng(seed_value);

% Step 2: Generating random numbers using randn
num_samples = 1000;
random_data = randn(1, num_samples);

% Step 3: Plotting the histogram for visualization
histogram(random_data, 'Normalization', 'probability');
title('Random Numbers from rand);
xlabel('Values');
ylabel('Probability');


% Step 4: Calculating mean and standard deviation
mean_value = mean(random_data);
std_deviation = std(random_data);


% Step 5: Displaying results
fprintf('Mean: %.4f\n', mean_value);
fprintf('Standard Deviation: %.4f\n', std_deviation);

Output: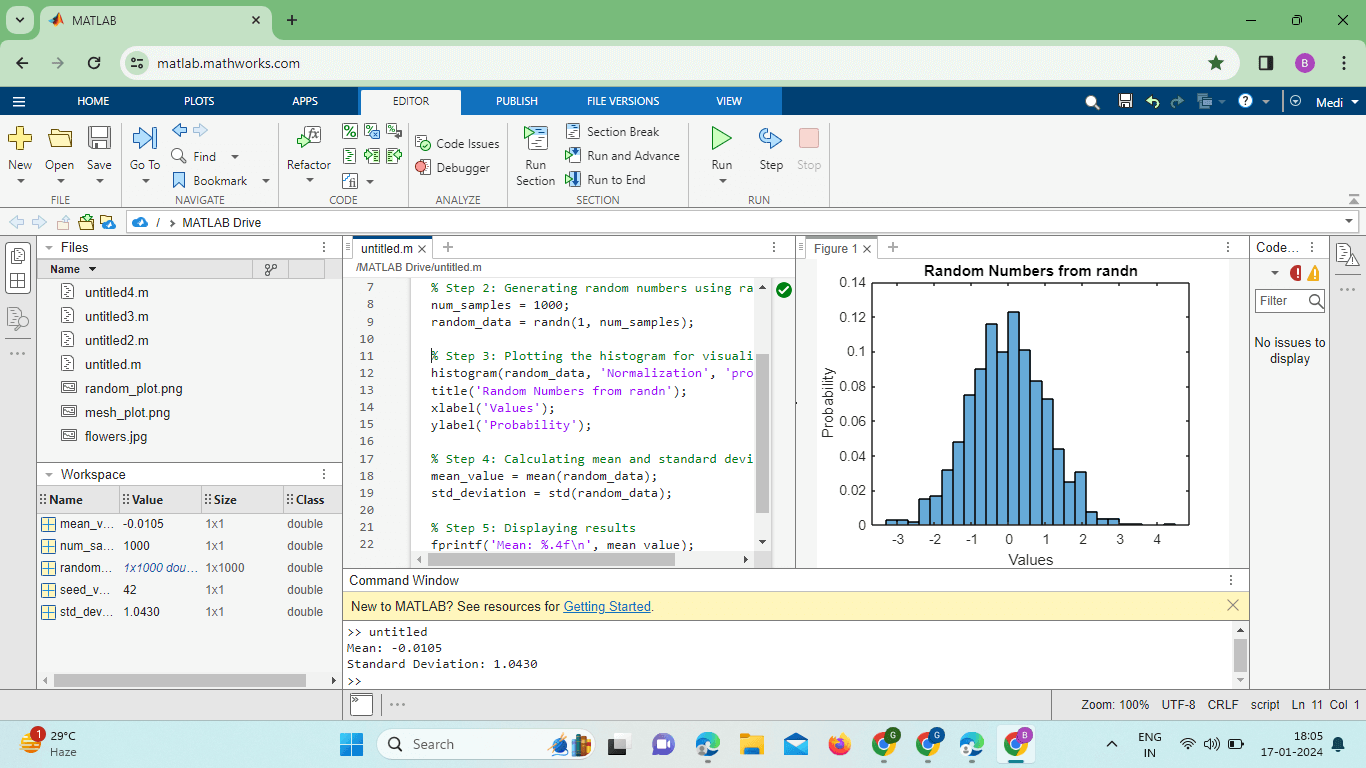

Explanation:

Setting Seed for Reproducibility (Optional): Setting the seed using rng is optional but ensures reproducibility. If you want the same sequence of random numbers every time you run the program, you can set a seed value.

Generating Random Numbers Using ran: dnThe randn function is then used to generate an array of random numbers. In this example, we generate 1000 random numbers conforming to a standard normal distribution.

Plotting the Histogram for Visualization: A histogram is created to visualize the distribution of the generated random numbers. The 'Normalization' option is set to 'probability' to display relative frequencies.

Calculating Mean and Standard Deviation: The mean and standard deviation of the generated random numbers are calculated using the mean and std functions.

Implementation:

% MATLAB Program: Generating Correlated Random Variables with randn
% Step 1: Setting seed for reproducibility (optional)
seed_value = 123;
rng(seed_value);

% Step 2: Generating correlated random variables
num_samples = 1000;
% Correlation matrix
correlation_coefficient = 0.6;


correlation_matrix = [1, correlation_coefficient; correlation_coefficient, 1];
% Cholesky decomposition to obtain correlated random variables
correlated_data = chol(correlation_matrix) * randn(2, num_samples);


% Step 3: Scatter plot for visualization
scatter(correlated_data(1, :), correlated_data(2, :), 20, 'filled');
title('Correlated Random Variables from rand);
xlabel('Variable 1');
ylabel('Variable 2');
axis equal;


% Step 4: Calculating sample correlation coefficient
sample_correlation = corrected(correlated_data(1, :), correlated_data(2, :));


% Step 5: Displaying results
fprintf('Desired Correlation Coefficient: %.2f\n', correlation_coefficient);
fprintf('Sample Correlation Coefficient: %.4f\n', sample_correlation(1, 2));

Output:

Explanation:

Setting Seed for Reproducibility (Optional): Similar to the previous example, setting the seed ensures reproducibility.
Generating Correlated Random Variables: We generate correlated random variables using the randn function and the Cholesky decomposition of the correlation matrix.
Scatter Plot for Visualization: A scatter plot is created to visualize the correlation between the two variables.
Calculating Sample Correlation Coefficient: The sample correlation coefficient is calculated using the corrected function.

Next TopicMATLAB text()

← prev next →