MATLAB Simpson's RuleThe trapezoidal and Simpson's rules are special cases of the Newton-Cote rules which use higher degree functions for numerical integration. Let the parabola represent the curve of the figure. y=αx2+βx+γ…………..equation 1 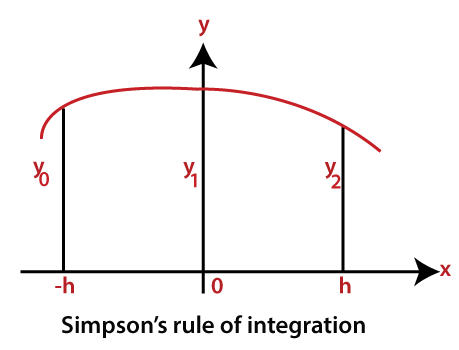
The area under this method for the interval -h≤x≤h is 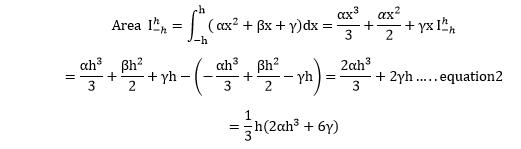
The curve passes through the three points(-h,y0 ),(0,y1 ),and (h,y2 ). Then, by an equation, we have: 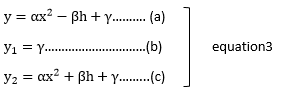
We can now evaluate the coefficients α,β,γ and express equation2 in terms of h, y0, y1and y2. This is done with the following procedure.By substitution of (b) of equation3 into (a) and (c) and rearranging we obtain αx2-βh=y0-y1…..equation4 αx2+βh=y2-y1…..equation5 Adding of equation4 with equation 5 yields 2αh2=y0-2y1+y2…...equation6 and by substitution into equation2, we obtain 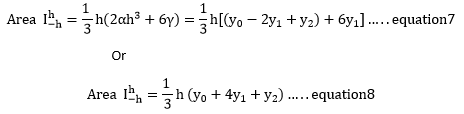
Now, we can apply equation8 to successive segments of any curve y=f(x) in the interval a≤x≤b as shown on the curve of the figure. 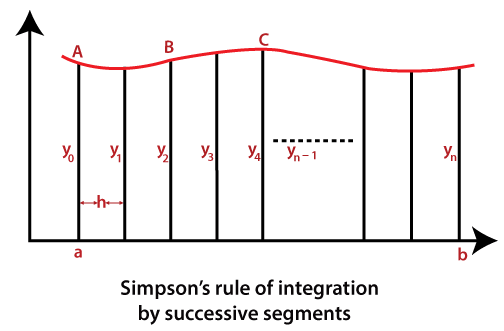
We observe that a parabola can approximate each segment of width 2h of the curve through its ends and its midpoint. Thus, the area under segment AB is 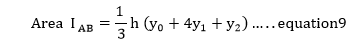
Likewise, the area under segment BC is 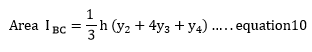
and so on. When the areas under each segment are added, we obtain 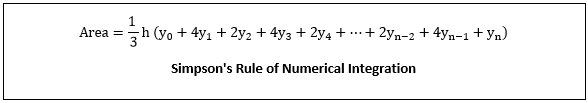
Since each segment has width 2h, to apply Simpson's rule of numerical integration, the number n of subdivisions must be even. This restriction does not apply to the trapezoidal rule of numerical integration. The value of for equation11 is found from 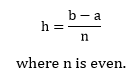
Next TopicMATLAB GUI
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









