MATLAB Unique

Introduction

The unique function in MATLAB is a powerful tool for identifying and extracting unique elements from arrays, cell arrays, and tables. Its flexibility in handling different data types and providing additional information about indices makes it a valuable asset in various applications.

One such versatile function is unique, which plays a crucial role in identifying and extracting unique elements from arrays or tables, eliminating duplicates. In this comprehensive guide, we'll explore the syntax, applications, and nuances of the unique function in MATLAB.

Syntax of the Unique Function

The unique function in MATLAB has a general syntax as follows:

A: Input array or vector.

C: Vector of unique values in the input array A.

a: Index vector that maps the values in C to the corresponding values in the input array A.

ic: Index vector that maps each element in the input array A to its corresponding value in C.

The output of the unique function provides not only the unique values in the Array but also information about their indices.

Basic Usage

Let's start with a simple example to illustrate the basic usage of the unique function:

% Creati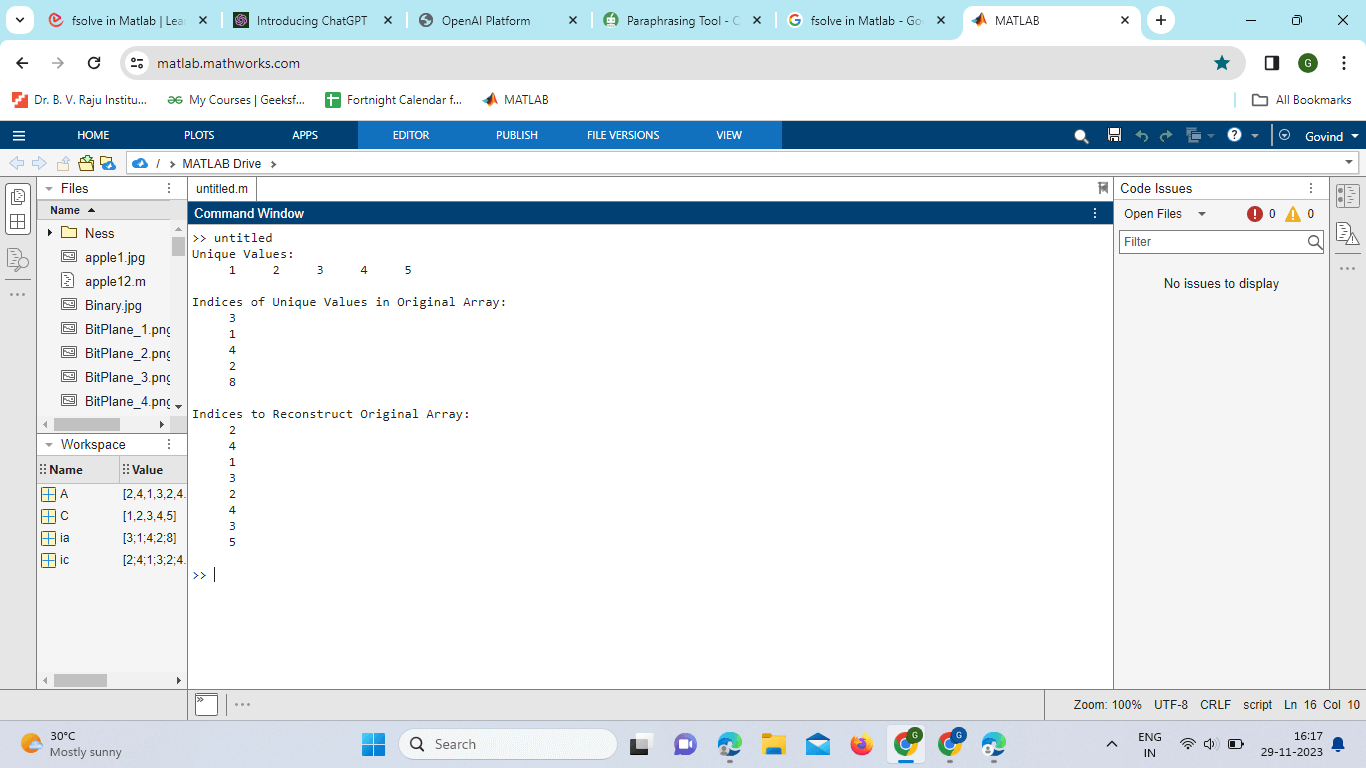ng an array with duplicate values
A = [2, 4, 1, 3, 2, 4, 3, 5];

% Using the unique function
[C, ia, ic] = unique(A);

% Displaying the unique values
disp('Unique Values:');
disp(C);

% Displaying the indices of unique values in the original Array
disp('Indices of Unique Values in Original Array:');
disp(ia);

% Displaying the indices to reconstruct the original Array from unique values
disp('Indices to Reconstruct Original Array:');
disp(ic);

Output:

Explanation:

In this example, Array A contains duplicate values, and the unique function is applied to it. The unique values are stored in vector C, the indices of these values in the original Array are stored in vector ia, and the indices to reconstruct the original Array from unique values are stored in the vector ic.

Array Creation:

A = [2, 4, 1, 3, 2, 4, 3, 5];

An array named A is created with eight elements, some of which are duplicates.

Applying unique to the Array:

[C, ia, ic] = unique(A);

C: Contains the unique values of the original Array.

ia: Contains the indices of the unique values in the original Array.

ic: Contains the indices to reconstruct the original Array from unique values.

Displaying Unique Values:

disp('Unique Values:');

disp(C);

This displays the unique values found in the array A.

Displaying Indices of Unique Values in Original Array:

disp('Indices of Unique Values in Original Array:');

disp(ia);

This displays the indices of the unique values in the original Array. It shows the positions of the unique values within the original Array.

Displaying Indices to Reconstruct Original Array:

disp('Indices to Reconstruct Original Array:');

disp(ic);

This displays the indices that can be used to reconstruct the original Array from the unique values. It provides a way to map back from the unique values to the original Array.

Handling Different Data Types

One of the strengths of the unique function is its ability to handle various data types. It is not limited to numeric arrays; it can be applied to character arrays, cell arrays, and even tables.

Example with Character Array

% Creati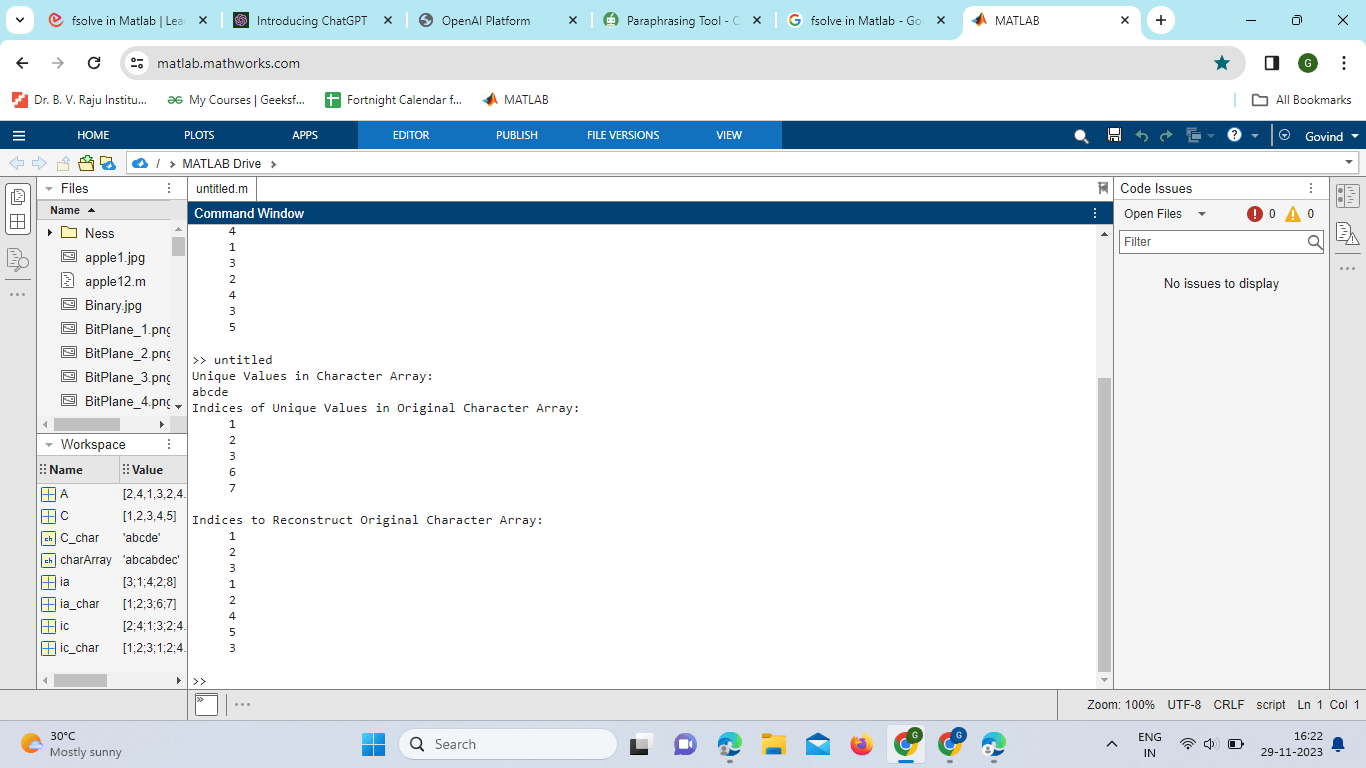ng a character array with duplicate values
charArray = ['a', 'b', 'c', 'a', 'b', 'd', 'e', 'c'];

% Using the unique function
[C_char, ia_char, ic_char] = unique(char array);

% Displaying the unique values in the character array
disp('Unique Values in Character Array:');
disp(C_char);

% Displaying the indices of unique values in the original character array
disp('Indices of Unique Values in Original Character Array:');
disp(ia_char);

% Displaying the indices to reconstruct the original character array from unique values
disp('Indices to Reconstruct Original Character Array:');
disp(ic_char);

Output:

In this example, a character array is used as input to the unique function. The same principles apply, and the output vectors C_char, ia_char, and ic_char provide information about the unique values and their indices.

Example with Cell Array

% Creati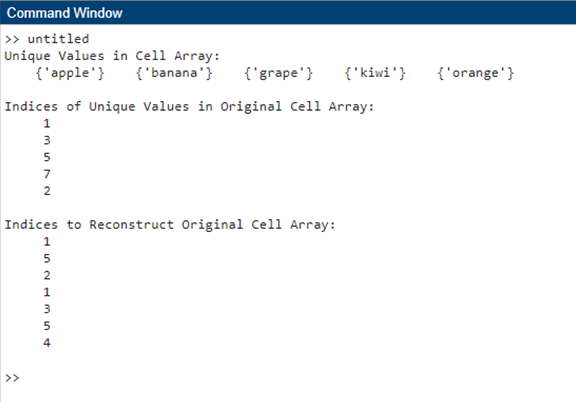ng a cell array with duplicate values
cell array = {'apple,' 'orange,' 'banana,' 'apple,' 'grape,' 'orange,' 'kiwi'};

% Using the unique function
[C_cell, ia_cell, ic_cell] = unique(cell array);

% Displaying the unique values in the cell array
disp('Unique Values in Cell Array:');
disp(C_cell);

% Displaying the indices of unique values in the original cell array
disp('Indices of Unique Values in Original Cell Array:');
disp(ia_cell);

% Displaying the indices to reconstruct the original cell array from unique values
disp('Indices to Reconstruct Original Cell Array:');
disp(ic_cell);

Output:

Here, a cell array containing strings is processed using the unique function. The resulting vectors provide insights into the unique values and their positions.

Advanced Options

The unique function in MATLAB also offers advanced options to customize its behavior based on specific requirements.

Sorting the Output

By default, the unique function returns the unique values in the order they appear in the input array.

However, it can be useful to sort the output. This can be achieved using an additional argument:

Example:

% Creati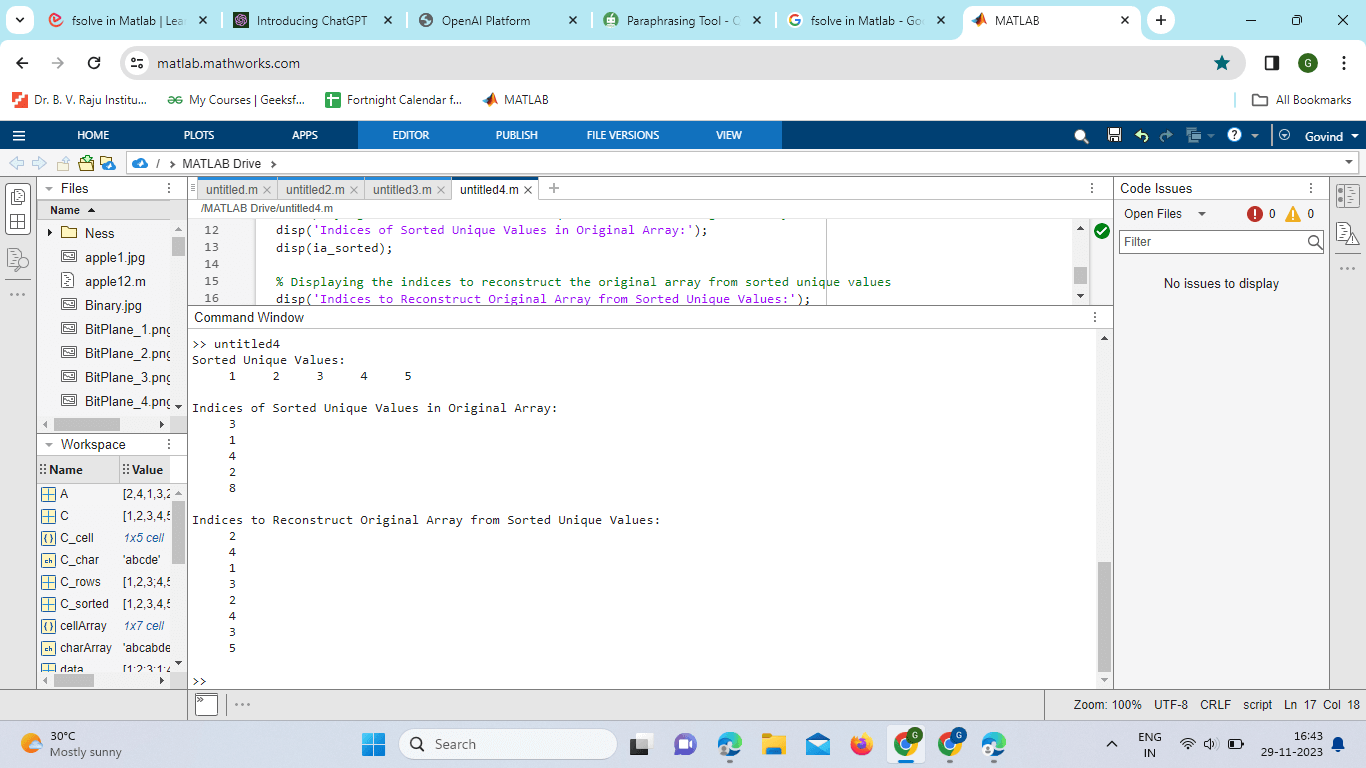ng an array with duplicate values
A = [2, 4, 1, 3, 2, 4, 3, 5];

% Using the unique function with sorting
[C_sorted, ia_sorted, ic_sorted] = unique(A, 'sorted');

% Displaying the sorted unique values
disp('Sorted Unique Values:');
disp(C_sorted);

% Displaying the indices of sorted unique values in the original Array
disp('Indices of Sorted Unique Values in Original Array:');
disp(ia_sorted);

% Displaying the indices to reconstruct the original Array from sorted unique values
disp('Indices to Reconstruct Original Array from Sorted Unique Values:');
disp(ic_sorted);

Output:

In this example, the 'sorted' option is used to obtain the unique values in sorted order.

Stable Sorting

Sometimes, it is important to maintain the order of appearance for the first occurrence of each unique value.

The 'stable' option can be used for this purpose:

% Creati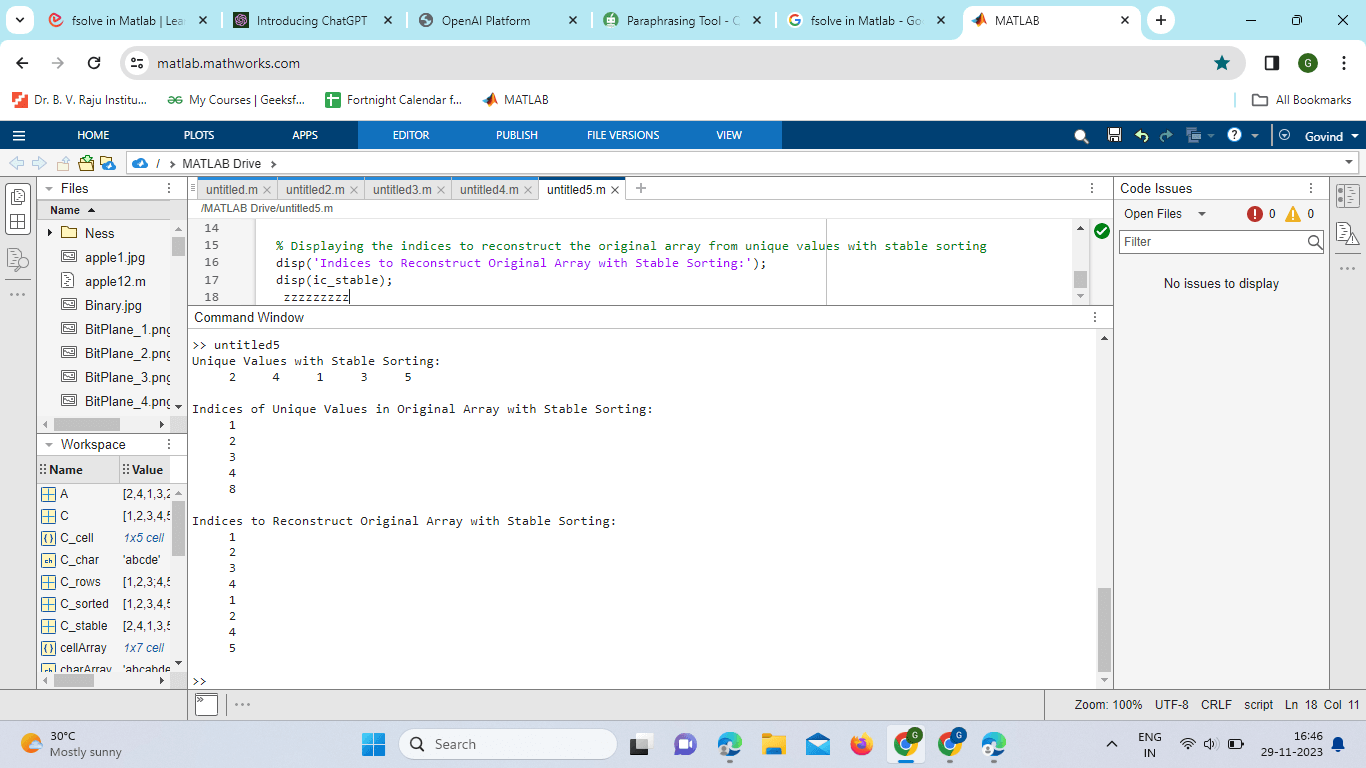ng an array with duplicate values
A = [2, 4, 1, 3, 2, 4, 3, 5];

% Using the unique function with stable sorting
[C_stable, ia_stable, ic_stable] = unique(A, 'stable');

% Displaying the unique values with stable sorting
disp('Unique Values with Stable Sorting:');
disp(C_stable);

% Displaying the indices of unique values in the original Array with stable sorting
disp('Indices of Unique Values in Original Array with Stable Sorting:');
disp(ia_stable);

% Displaying the indices to reconstruct the original Array from unique values with stable sorting
disp('Indices to Reconstruct Original Array with Stable Sorting:');
disp(ic_stable);

Output:

Here, the 'stable' option ensures that the order of the first occurrence of each unique value is maintained.

Rows or Columns

Example:

The unique function can be applied to either rows or columns of a matrix by specifying the 'rows' or 'columns' option:

% Creati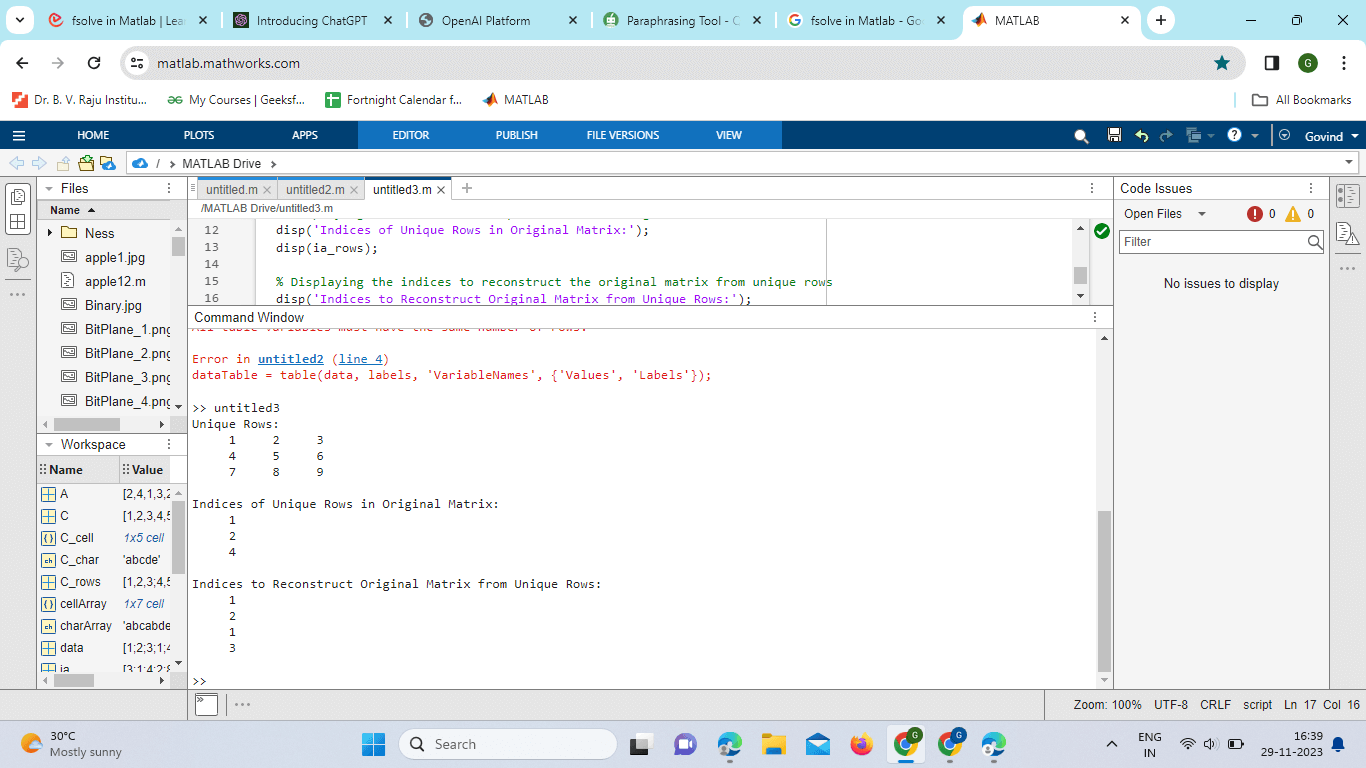ng a matrix with duplicate rows
matrix = [1, 2, 3; 4, 5, 6; 1, 2, 3; 7, 8, 9];

% Using the unique function on rows
[C_rows, ia_rows, ic_rows] = unique(matrix, 'rows');

% Displaying the unique rows
disp('Unique Rows:');
disp(C_rows);

% Displaying the indices of unique rows in the original matrix
disp('Indices of Unique Rows in Original Matrix:');
disp(ia_rows);

% Displaying the indices to reconstruct the original matrix from unique rows
disp('Indices to Reconstruct Original Matrix from Unique Rows:');
disp(ic_rows);

Output:

Explanation:

In this example, the unique function is applied to the rows of a matrix using the 'rows' option.

Matrix Creation:

matrix = [1, 2, 3; 4, 5, 6; 1, 2, 3; 7, 8, 9];

A matrix named matrix is created with four rows and three columns. The first and third rows are identical.

Applying unique to Rows:

[C_rows, ia_rows, ic_rows] = unique(matrix, 'rows');

C_rows: Contains the unique rows of the original matrix.

ia_rows: Contains the indices of the unique rows in the original matrix.

ic_rows: Contains the indices to reconstruct the original matrix from unique rows.

Displaying Unique Rows:

disp('Unique Rows:');

disp(C_rows);

This displays the unique rows found in the matrix variable.

Displaying Indices of Unique Rows in Original Matrix:

disp('Indices of Unique Rows in Original Matrix:');

disp(ia_rows);

This displays the indices of the unique rows in the original matrix. In other words, it shows the positions of the unique rows within the original matrix.

Displaying Indices to Reconstruct Original Matrix:

disp('Indices to Reconstruct Original Matrix from Unique Rows:');

disp(ic_rows);

The code demonstrates how to identify and extract unique rows from a matrix using the unique function with the 'rows' option in MATLAB. The resulting unique rows, their indices in the original matrix, and indices to reconstruct the original matrix are then displayed.

Performance Considerations

When dealing with large datasets, the performance of the unique function becomes a crucial factor. Understanding the underlying mechanisms can help optimize its usage.

Time Complexity

The time complexity of the unique function depends on the algorithm used. MATLAB employs different algorithms based on the characteristics of the input data. For example, sorting algorithms are used when the data is numeric or character, and hashing is used for cell arrays.

Memory Usage

Memory consumption is another important consideration, especially when dealing with large datasets. Sorting algorithms may require additional memory, and this can impact the performance of the function.

Vectorization

Taking advantage of MATLAB's vectorized operations can significantly improve the performance of the unique function. Vectorized code is optimized for array operations, and MATLAB is designed to perform these operations efficiently.

Vectorized operations often outperform their loop-based counterparts in MATLAB.

Understanding the syntax and advanced options of the unique function allows users to tailor its behavior to specific requirements. Whether dealing with numeric arrays, character arrays, cell arrays, or tables, the unique function provides a consistent and efficient way to handle duplicate values in MATLAB.

When working with large datasets, it's essential to consider the performance implications of the unique function.
Optimizing code by taking advantage of vectorized operations and being aware of the underlying algorithms can lead to significant improvements in execution time and memory usage.

Next TopicMatlab Colon

← prev next →