PermLAB

Introduction:

A low-pass filter in MATLAB is a digital signal processing technique intended to attenuate or block higher frequencies while permitting lower-frequency signals to flow through. In order to expose the underlying trends in the signal, high-frequency components like noise or abrupt changes must be suppressed or removed in situations where this filtering process is essential.

What is a Low-Pass Filter?

A low-pass filter is an electronic circuit or algorithm designed to allow signals with a frequency lower than a specified cutoff frequency to pass through while attenuating or blocking higher frequencies. This is crucial in scenarios where high-frequency noise needs to be removed, and only the essential, lower-frequency components of a signal are of interest.

Importance of Low-Pass Filters

Low-pass filters serve various purposes in signal processing, communication systems, and image processing. They help eliminate high-frequency noise, reduce data transmission errors, and enhance the clarity of signals. In MATLAB, the 'dp.LowpassFilter' command is a powerful tool for implementing low-pass filters.

Frequency Elements

Various frequency components are frequently combined to form signals. Low-pass filters isolate slower-varying or important parts of the signal by selectively focusing on higher-frequency components.

Cutoff Wavelength:

One important low-pass filter parameter is the cutoff frequency. It indicates the frequency at which the filter attenuates higher frequencies. To establish and modify this parameter in accordance with the particular needs of the signal processing activity, MATLAB offers tools.

Types of low pass filter:

Low-pass filters that attenuate higher-frequency signals while allowing low-frequency signals to flow through are crucial parts of electronic circuits.

The inductor, which is the main component of these filters, effectively suppresses high-frequency signals due to its high impedance.

Inductive Low-Pass Filters

Inductive low-pass filters use inductors to attenuate higher frequencies. These filters are common in audio applications, where they can help remove high-frequency interference while allowing the desired low-frequency audio signals to pass through. MATLAB offers versatile tools for designing and simulating inductive low-pass filters.

Capacitive Low-Pass Filters

Capacitive low-pass filters, on the other hand, employ capacitors to achieve signal attenuation. These filters find applications in electronic circuits and communication systems, where they effectively block high-frequency noise. MATLAB's capabilities make it an ideal environment for designing and analyzing capacitive low-pass filters.

Implementation in MATLAB:

Design: Inductive low-pass filter design tools are available in MATLAB. For filter design, the Signal Processing Toolbox and the disinfect function are frequently utilized.

Simulation and Analysis: The frequency response of inductive low-pass filters can be simulated and examined by engineers using MATLAB. This helps to optimize the filter settings for certain uses.

Design Points to Remember:

Inductor Selection: Selecting the right inductor requires taking into account a number of variables, including saturation characteristics, current-carrying capability, and inductance value. For better filter performance, high-quality inductors with low resistance and parasitic capacitance are frequently recommended.

Filter Order: The roll-off's steepness is influenced by the filter order. Although they may require more complicated components, higher-order filters attenuate higher frequencies more aggressively.

Getting Started with 'dp.LowpassFilter'

MATLAB simplifies the implementation of low-pass filters through the 'dp.LowpassFilter' command. This command provides a user-friendly interface for designing and applying low-pass filters to signals. Users can specify parameters such as cutoff frequency, filter order, and filter type.

Syntax and Parameters

Understanding the syntax of the 'dp.LowpassFilter' command is essential for effective implementation. Parameters such as 'CutoffFrequency,' 'FilterOrder,' and 'FilterType' play a crucial role in shaping the characteristics of the low-pass filter. Practical examples will be provided to illustrate the impact of these parameters on filter performance.

Designing Custom Low-Pass Filters

While 'dp.LowpassFilter' offers convenience, there are instances where custom filters are necessary. MATLAB's signal processing toolbox provides functions for designing custom filters based on specific requirements. We will explore the design process and demonstrate how to implement custom low-pass filters in MATLAB.

Applications and Examples

Signal Denoising

One common application of low-pass filters is signal denoising. MATLAB's ability to apply low-pass filters to noisy signals will be showcased. Examples will include audio signals and biomedical data, demonstrating how low-pass filtering enhances signal clarity by reducing high-frequency noise.

Image Processing

In image processing, low-pass filters are employed to smooth images and remove high-frequency details. MATLAB's image processing toolbox integrates seamlessly with the 'dp.LowpassFilter' command, allowing users to apply low-pass filters to images for various applications, such as blurring and feature extraction.

Right Filter Parameters

Selecting appropriate filter parameters is crucial for achieving the desired filtering effect. We will discuss best practices for choosing cutoff frequencies, filter orders, and types based on the specific characteristics of the input signals.

Constituents and Features:

C-type Capacitor:

Within their electric fields, capacitors store and discharge electrical energy. Capacitors are used to short-circuit higher-frequency signals in capacitive low-pass filters effectively.

A capacitor can conduct more effectively at higher frequencies because its impedance lowers with frequency.

Resistance (R): To regulate the total impedance and mold the filter response, the circuit may use a series resistor.

The resistor aids in optimizing the filter's properties and reducing the filter's response.

Reaction to Frequency:

Cutoff Frequency: The cutoff frequency of capacitive low-pass filters is the same as that of inductive filters. Low-frequency signals can travel through the capacitor below this frequency with little to no attenuation.

Higher-frequency components are effectively shorted out by the capacitor's decreasing impedance beyond the cutoff frequency.

Roll-off: The filter's sequence affects how quickly higher frequencies are attenuated after the cutoff point.

Higher-order filters suppress high-frequency components more well because of their steeper roll-off characteristics.

Uses:

Audio Signal Filtering: Only the intended low-frequency audio signals are transferred when high-frequency noise and undesired harmonics are removed from audio systems using capacitive low-pass filters.

Radio Frequency (RF) Signal Processing: Capacitive low-pass filters can be used in RF applications to filter out undesired harmonics and high-frequency interference.

For the efficient suppression of high-frequency components in a wide range of electronic applications, capacitive low-pass filters are indispensable. Engineers working on electronic circuits and signal processing applications need to understand the design concepts, features, and factors related to capacitive low-pass filters. The flexible tools in MATLAB make it much easier to create, simulate, and analyze these filters for particular engineering applications.

Implementation:

Output: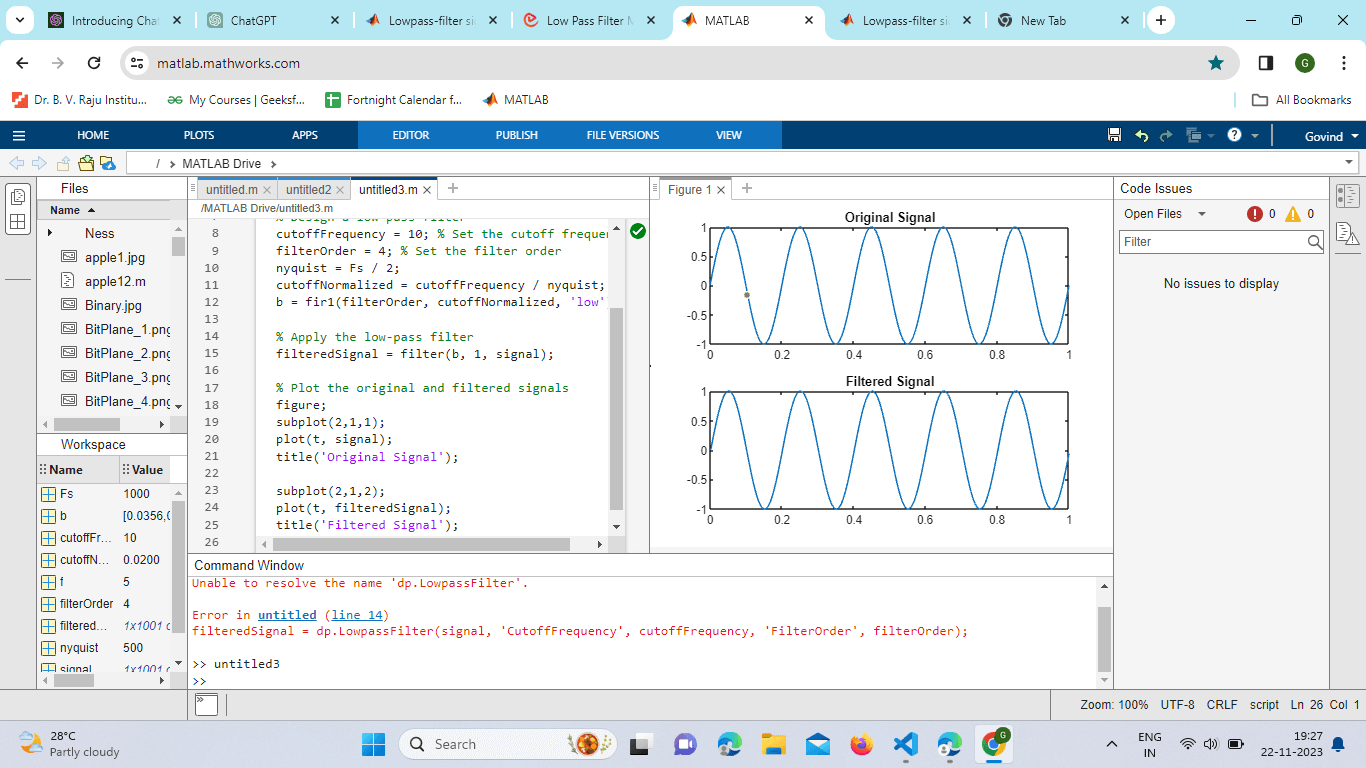

Explanation:

Design of Low-Pass Filter: CutoffThe frequency at which the filter attenuates signals is 10 Hz; that's where it's placed.

The filter's complexity is determined by setting filterOrder to 4.

Half of the sampling frequency is known as the Nyquist frequency or Nyquist.

cut-offBy dividing the cutoff frequency by the Nyquist frequency, one can obtain the normalized cutoff frequency.

A low-pass FIR filter (b) with the required filter order and normalized cutoff frequency is designed using fir1.

Program:

Output:

Explanation:

Open an Illustrated Image:

I read the original image as "apple1.jpg"; 'apple1.jpg' is the sample image that is loaded into the variable origin.

Transform the Picture into Grayscale:

grayImage = rgb2gray(originalImage);: Stores the grayscale version of the loaded color image (originalImage) in grayImage.

How to Make a Low-Pass Filter:

Cutoff frequency = 0.1; Adjusts the low-pass filter's cutoff frequency. Adapt this parameter to suit your needs.

filterOrder = 4;: Indicates the filter's order.

How to Make a Gaussian Filter

special ('gaussian,' [filterOrder*2+1, filterOrder*2+1], cutoffFrequency); gaussian filter =; makes use of the special function to create a Gaussian filter. In both dimensions, filterOrder*2+1 determines the filter size.

Use the Low-Pass Filter to Smooth Images:

smoothedImage = filter (double(grayImage), gaussian filter, 'replicate');: The grayscale image is smoothed by applying the Gaussian filter. Image borders are handled using the ' replicate' option.