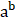Matrices and Arrays in MATLAB
- MATLAB operates on whole matrices and arrays at a time.
- All types of data variables are stored as multidimensional arrays, let it be a character, string, or numbers.
- A two-dimensional array is called a matrix often used for linear algebra.
Array creation in MATLAB
We can create arrays in multiple ways in MATLAB:
- By using space in between elements:
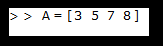
- This command creates an array variable 'A' having one row and four columns.
- 'A' variable stored in the workspace and the output will be displayed in the command window as:
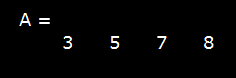
- By using comma in between elements:
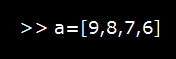
- This command will create an array variable 'a' having one row and four columns.
- 'a' variable stored in the workspace, and the output will be displayed in the command window as:

- We can combine both approaches into one, but this is not a good practice.
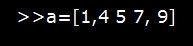
It will work the same as before, but avoid it for better syntax.
- The array having its elements in a single row is known as a row vector. Or we can say a single-dimensional array is a vector.
- A two-dimensional array is called a matrix. It means a matrix has multiple rows and columns. So, while creating a matrix with multiple rows, we have to separate the rows with semicolons.
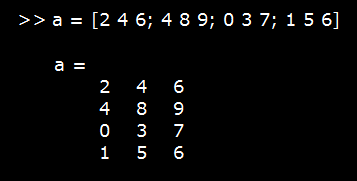
- Be careful while creating a matrix, each row should have the same number of columns, and each row should be separated with a semicolon. Otherwise, it will show error and won't create the matrix.

- We can create a matrix by using the in-built function, such as ones, zeros, or rand.

Matrix and Array Operations in MATLAB
MATLAB support two categories of operations between arrays, known as array operations and matrix operations.
Array operations are operations implemented between arrays on an element-by-element basis. That is, the operation is implemented on corresponding elements in the two arrays.
For example,
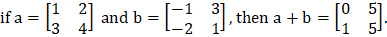
Note: The number of row and columns in both arrays must be the same. If not, MATLAB will generate an error message.
The following table provides a summary of arithmetic operations between two scalars in MATLAB.
Arithmetic Operations between two Scalars
| Operation |
Algebraic Form |
MATLAB Form |
| Addition |
a + b |
a + b |
| Subtraction |
a - b |
a - b |
| Multiplication |
a x b |
a * b |
| Division |
 |
a / b |
| Exponentiation |
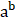 |
a ^ b |
Array operations may also appear between an array and a scalar. If the operation is performed between an array and a scalar, the value of the scalar is applied to every element of the array.
For example,
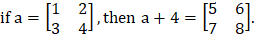
Matrix Operations
Matrix operations follow the standard rules of linear algebra, such as matrix multiplication. In linear algebra, the product c=a x b is defined by the equation.
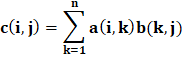
For example,
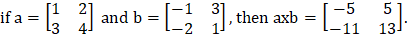
Note: The number of columns in the matrix a must be equal to the number of rows in matrix b.
MATLAB uses a special symbol to categorize array operations from matrix operations. In the method where array operations and matrix operations have a different definition, MATLAB uses a period before the symbol to indicate an array operation (for example, .*).
A list of the standard array and matrix operations is given in the table.
| Operation |
MATLAB Form |
Comments |
| Array Addition/td>
| a+b/td>
| Array addition and matrix addition are identical. |
| Array Subtraction/td>
| a-b/td>
| Array subtraction and matrix subtraction are identical. |
| Array Multiplication/td>
| a .* b/td>
| Element-by-Element multiplication of a and b. Both array must be the same shape, and one of them must be a scalar. |
| Matrix Multiplication/td>
| a*b/td>
| Matrix multiplication of a and b. The number of column in a must equal the number of rows in b. |
| Array Right Division/td>
| a ./ b/td>
| Element-by-element division of a and b: a (i, j) / b (i, j). Both arrays must be the same shape, and one of them must be a scalar. |
| Array Left Division/td>
| a .\ b/td>
| Element-by-element division of a and b, but with b in the numerator: b(i,j) / a(i,j). Both arrays must be the same shape, and one of them must be a scalar. |
| Matrix Right Division/td>
| a/b/td>
| Matrix division defined by a * inv (b), where inv(b) is the inverse of matrix b. |
| Matrix Left Division/td>
| a\b/td>
| Matrix division defined by inv(a) * b, where inv(a) is the inverse of matrix a. |
| Array Exponentiation |
a .^ b/td>
| Element-by-Element exponentiation of a and b: a (i, j) ^ b (i, j). Both arrays must be the same shape, and one of them must be a scalar. |
Examples of Matrix and Array Operations
- We can process all of the values in a matrix using a single arithmetic operator.
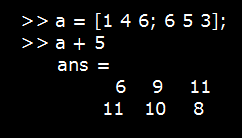
- One point to note here is that when we input the command as a + 5, it will not change the original variable 'a' till we don't assign it the output again.
- That's why the above output assigned to the default variable 'ans.'
- We can process the whole matrix using a single function, as well.

- We can enter a comment by using the '%' percentage sign before the comment line.
- Use single quote (') after the variable, to transpose the matrix.

- Transposing of matrix places each row as a column.
- In MATLAB, we can perform element-wise multiplication besides matrix multiplication.
Let's understand what is the difference between element-wise multiplication and matrix multiplication, with an example:

Format Command in MATLAB
MATLAB stores internally all numbers as floating-point values, up to 15 decimal points. But it usually displays up to 4 decimal points. Let's see with an example.
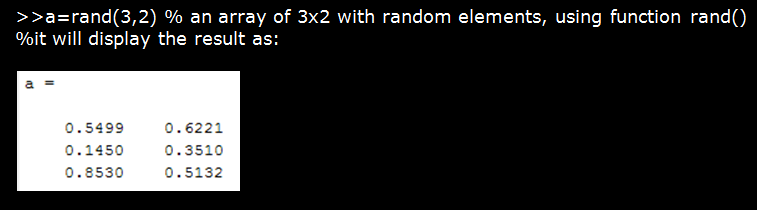
- Now we will use the format command to display the result up to maximum possible decimal points in MATLAB:
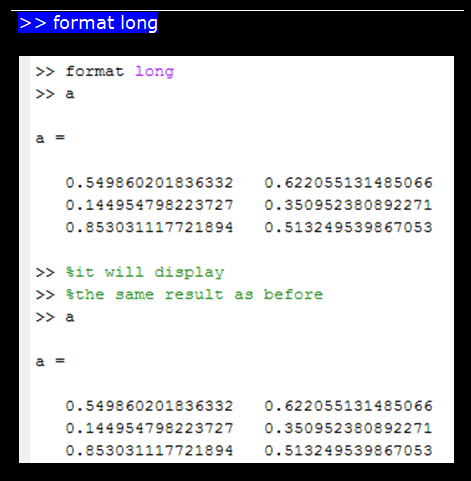
- Format command syntax: enter 'format long' at the command line.
- It will continue the above format until we change the format command.
- Now we will use another format command to change the format:

Concatenation of Arrays in MATLAB
As we concatenate or join the strings, in MATLAB, we can join the arrays also. The pair of square brackets [ ] used in the declaration of the array is itself a concatenation operator.
We can concatenate the arrays in two ways:
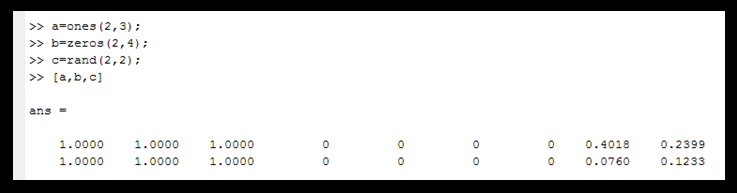
Horizontal Concatenation of Arrays in MATLAB
- Rule: all arrays should have the same number of rows.
- Syntax: enclose all arrays in square bracket separated by commas, [a, b, c].
- Example:
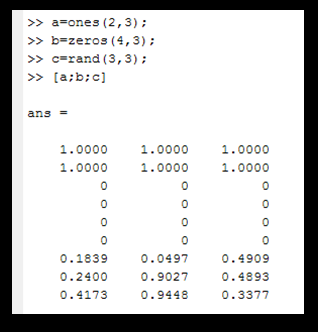
Vertical Concatenation of Arrays in MATLAB
- Rule: all arrays should have the same number of columns.
- Syntax: enclose all arrays in square bracket separated by semi-colons, [a;b;c].
- Example:
Denoting Complex Numbers in MATLAB
- Complex numbers have both real and imaginary parts.
- The value of the imaginary unit is equivalent to the square root of -1.
sqrt (-1) => 0.0000 + 1.0000i
- Use letter either 'i' or 'j' to represent the imaginary part of the complex number.
- Example:

Array Indexing in MATLAB
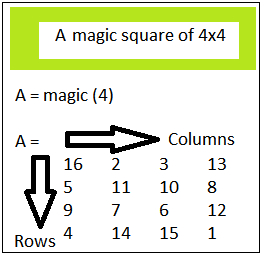
Every variable is an array in MATLAB. And all the elements in the array are indexed as per row and column. Any particular element can be accessed using indexing in MATLAB. The indexing in arrays in MATLAB is the same as mathematics. It has a different syntax of accessing the elements.
There are several ways of indexing elements in MATLAB.
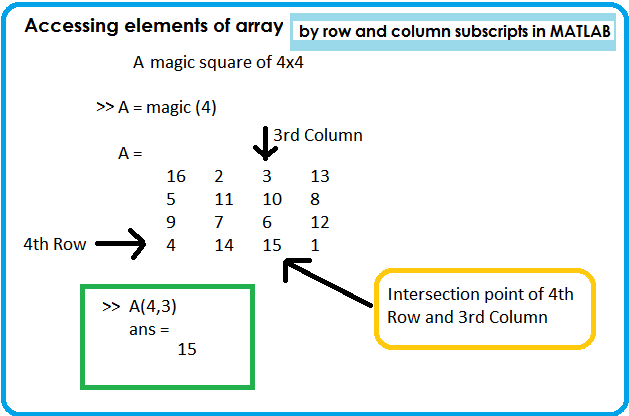
1. By specifying row and column subscripts:
- The most common way to refer particular components of an array is by specifying row and column subscripts in brackets with an array variable.
- The element s searched at the intersection point of row and column specified as the subscript.
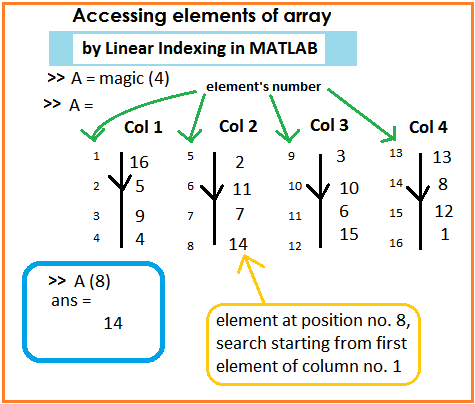
2. Linear Indexing in MATLAB
- The use of single subscript in-spite-of row and column subscript is called Linear Indexing in MATLAB.
- An element is searched traversing down each column in order.
3. Refer multiple elements of an Array in MATLAB
- There is one colon operator (:) in MATLAB, use it to refer multiple elements of an array.
- Example:



Vector Creation Using Colon Operator in MATLAB
By using the colon operator, we can create an equally spaced vector of values. We can assign step value that can affect the next value at a fixed interval.
- Syntax: start: step: end.
- Example:
Let's create a table of 13 with the help of the colon operator.

Accessing Array Elements Outside Current Dimension
- We can access elements only within the current dimension. It means if it is a vector and holds nine elements, then, we can't access the element at position 12. Because the 12th position was not defined during the vector creation.
- If we enter a command for accessing an element outside its' current dimension, then it will throw an error saying index exceeds array bounds.

- But we can assign a value to the position which is currently not available.
- For example, we have a vector of 9 elements; then, we can create a 12th element or any element beyond the 9th by assigning it the value.
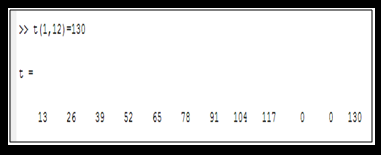
- And if there is any gap between the last index and the newly created index, then the gap index will be assigned a 0 value automatically.
- A value can be assigned to an index in all arrays.

|
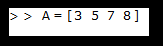
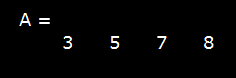
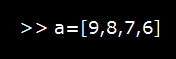





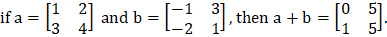
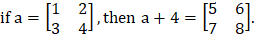
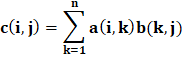
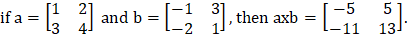




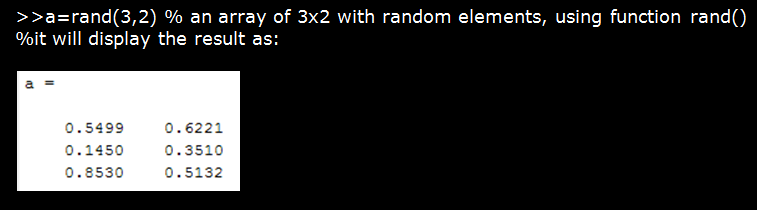















 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now