Edge Detection Using in-Built Function in MATLAB

An image processing method called edge detection is used to locate boundaries and edges in an image. The contours of objects or interesting areas might be represented by these edges, which frequently correspond to substantial changes in the image's intensity, colour, or texture. Edge detection's main objective is to draw attention to these sudden shifts, making extracting and evaluating an image's key elements simpler.

Edge detection is frequently used in various applications, including image analysis, object recognition, computer vision, and picture segmentation. It acts as a preprocessing step for tasks like object detection, picture compression, and pattern recognition.

About Edge:

You can select the edge feature in MATLAB from various edge detection algorithms. Some of these algorithms, like Sobel, Prewitt, and Roberts, are based on the first derivative of intensity to find sudden changes in intensity, while others, like Canny, use the second derivative criterion with zero crossing to detect edges more complexly. In many image processing and computer vision applications, identifying and highlighting edges or boundaries in images is a crucial step. These algorithms assist with this.

First Derivative Standard:

The intensity change rate at each pixel position is represented by an image's first derivative of intensity. Potential edges are regions of the image where the first derivative exceeds a predetermined threshold in magnitude. Using MATLAB's edge function, you may apply this criterion to several edge detection techniques, including the Sobel, Prewitt, and Roberts operators.

Sobel operator: The Sobel operator uses convolution with two 3x3 kernels, one for detecting changes in the horizontal direction (Sobel-X) and the other for changes in the vertical direction (Sobel-Y), to determine the gradient of the image. The gradient's size calculates the rate at which intensity changes.

Prewitt Operator: Like the Sobel operator, the Prewitt operator calculates the gradient in both the horizontal and vertical directions using convolution with 3x3 kernels.

Roberts Operator: The Roberts operator is a less complex operator that uses two 2x2 kernels to estimate the gradient.

When invoking the edge function, you can specify which operator to use, and it will compute the first derivative of intensity depending on that operator.

Second Derivative Criterion with Zero Crossing

The second intensity derivative measures the gradient's rate of change or the rate at which intensity changes from pixel to pixel. We are looking for areas in edge detection where this second derivative crosses the zero line. When the gradient's sign (from positive to negative or vice versa) changes, it indicates the presence of an edge when there is a zero crossing.

Canny Edge Detector: The Canny edge detector is one of the edge function methods in MATLAB that uses the second derivative criterion with zero crossing. The gradient's magnitude and direction are computed, and noise is reduced using Gaussian smoothing.

• Then, it uses hysteresis thresholding to connect neighbouring edge pixels into continuous edge contours and applies non-maximum suppression to thin edges.
• MATLAB includes several built-in edge detection functions that use various algorithms and methods to find image edges.

Sobel's Edge Detector:

The gradient of the image in both the horizontal and vertical directions is calculated by the Sobel edge detector using convolution with 3x3 kernels.

It draws attention to locations with a noticeable variation in intensity to emphasize edges.

Examples:

Output: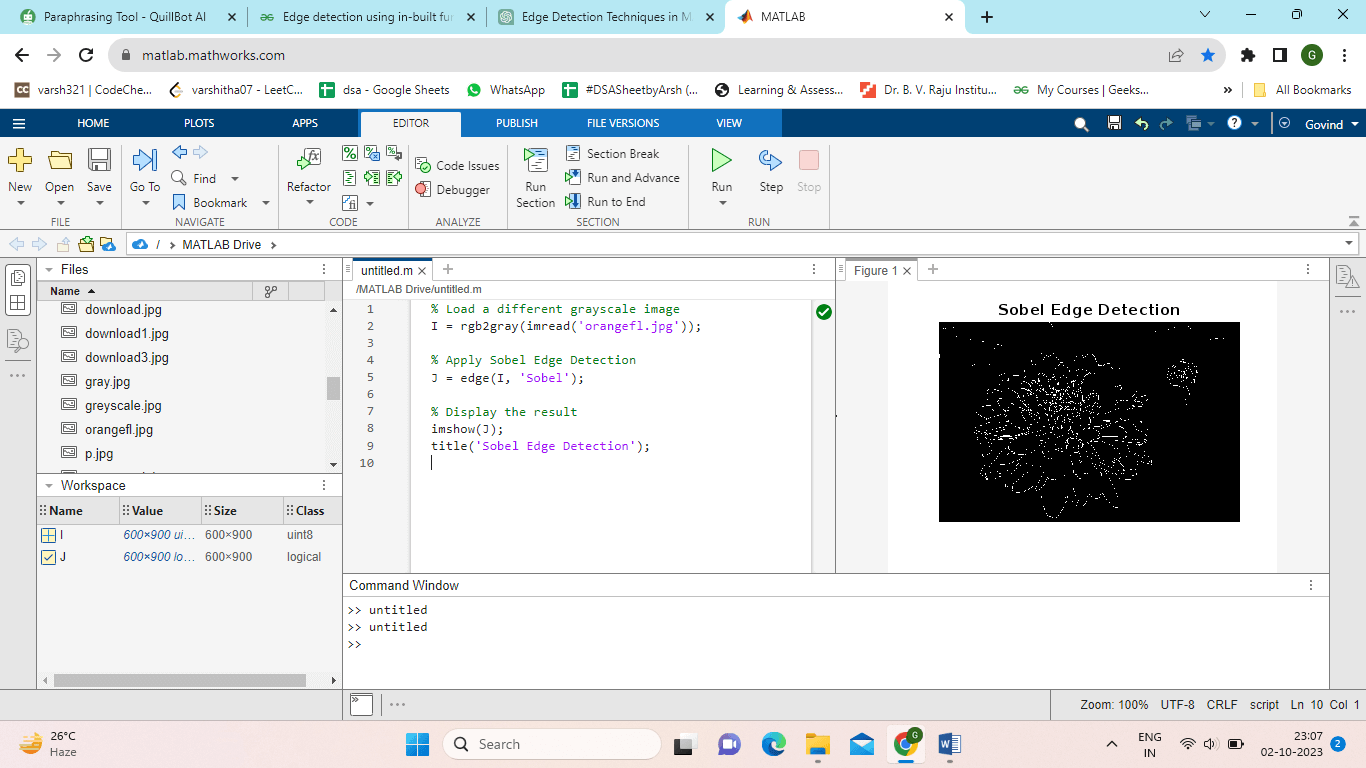

Edge Detector by Prewitt:

The Prewitt edge detector calculates the gradient in the horizontal and vertical directions using convolution with 3x3 kernels, much like the Sobel operator.

Images' edges are likewise highlighted with this technique.

Example:

Output: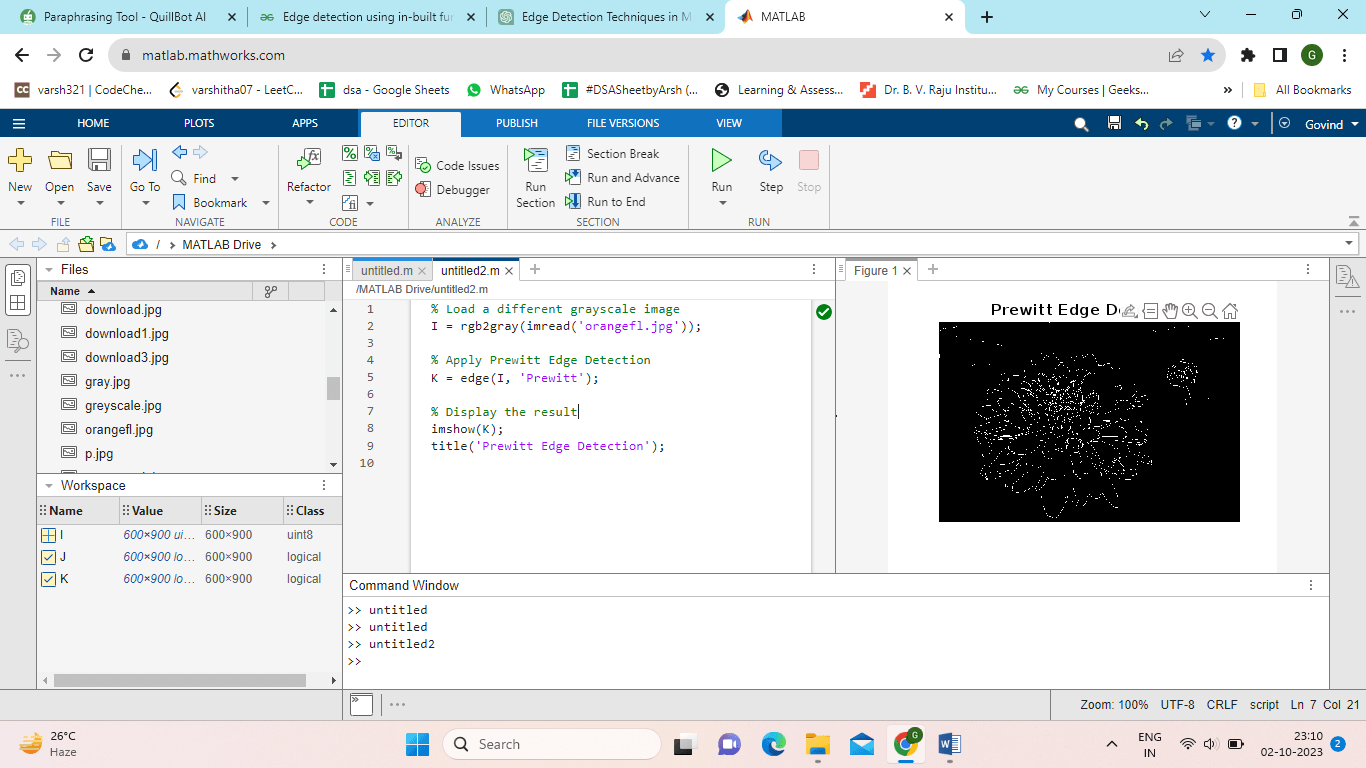

Edge Detector by Roberts:

A pair of 2x2 kernels are used by the Roberts edge detector, a less complex operator, to approximate the gradient.

A simple edge detection technique draws attention to sudden intensity fluctuations.

Example:

Output: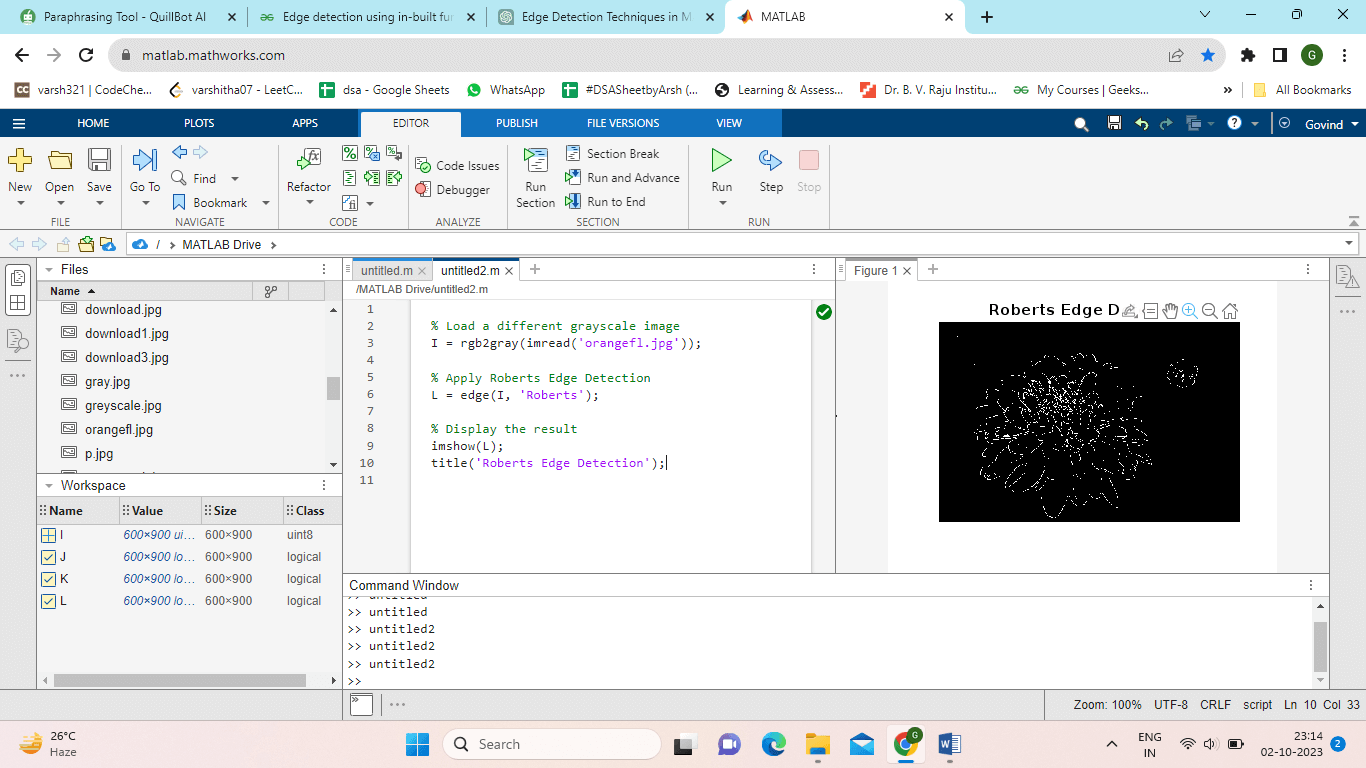

Edge Detector for Log (Laplacian of Gaussian):

The image is smoothed with a Gaussian algorithm by the Laplacian of Gaussian (LoG) edge detector before computing the Laplacian operator.

By seeing zero crossings in the Laplacian image, it is utilized to find edges.

Example:

Output: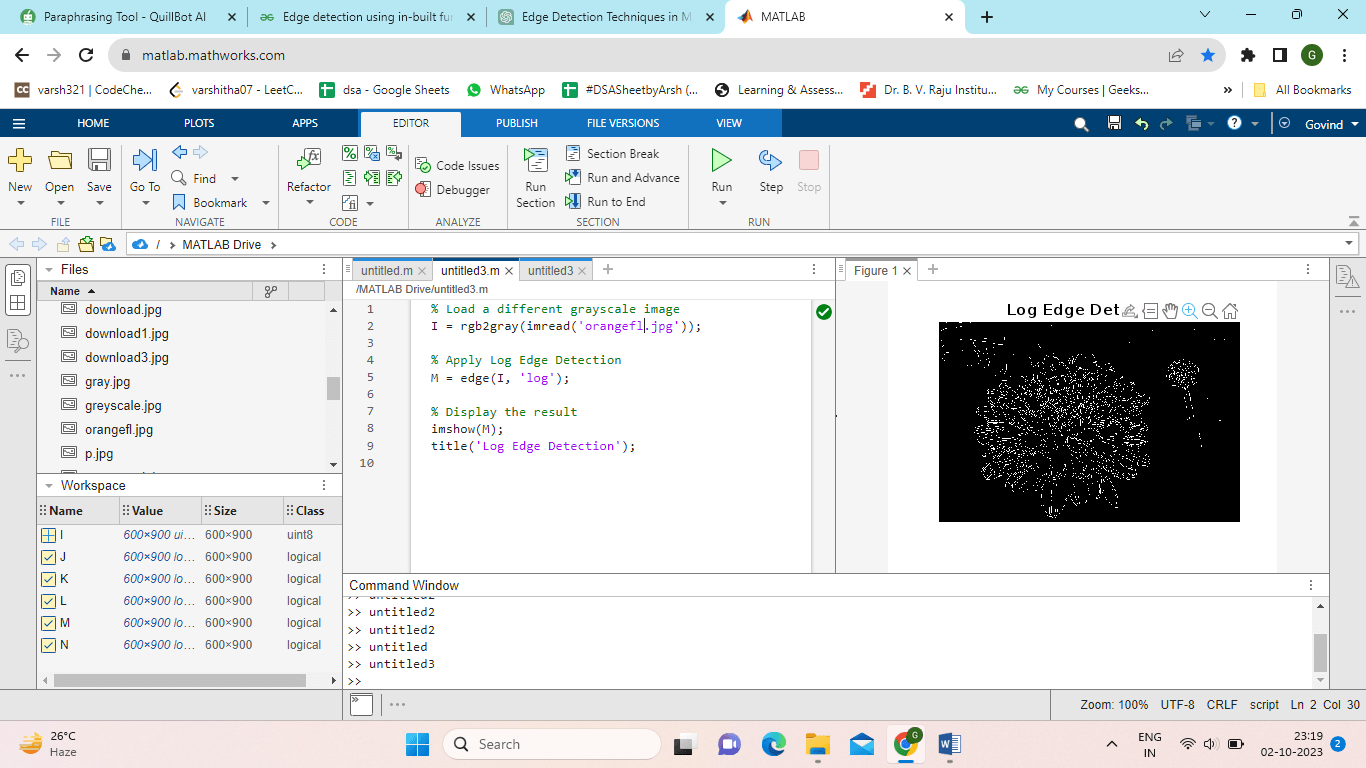

Detector of Zero Crossing Edge:

The zero-crossing edge detector generally uses the second intensity derivative to identify the locations where the gradient changes sign.

It can locate edges by seeing zero crossings in the gradient magnitude image.

output: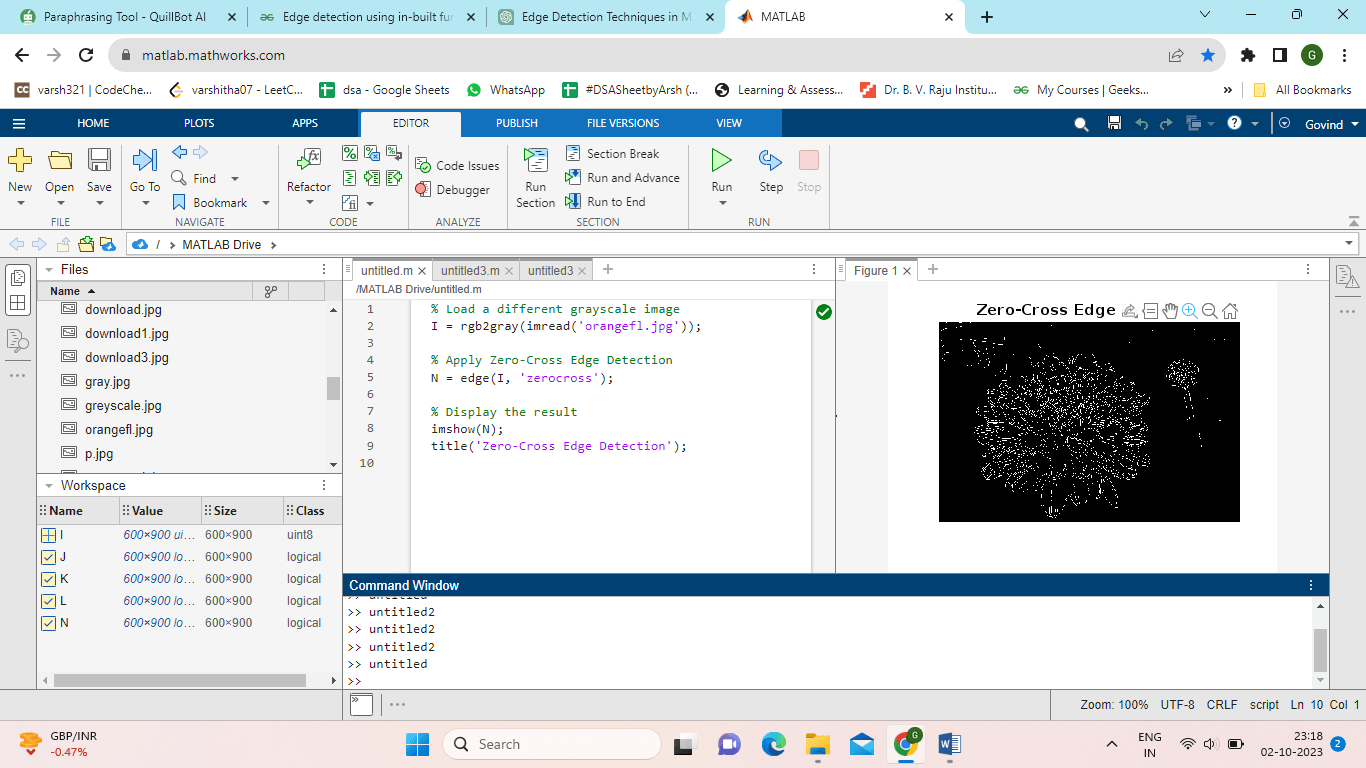

Indicator of Canny Edges:

A multi-stage edge detection algorithm is the Canny edge detector. It uses Gaussian smoothing, gradient calculation, non-maximum suppression, and hysteresis thresholding

to detect edges while minimizing noise precisely.

• Each edge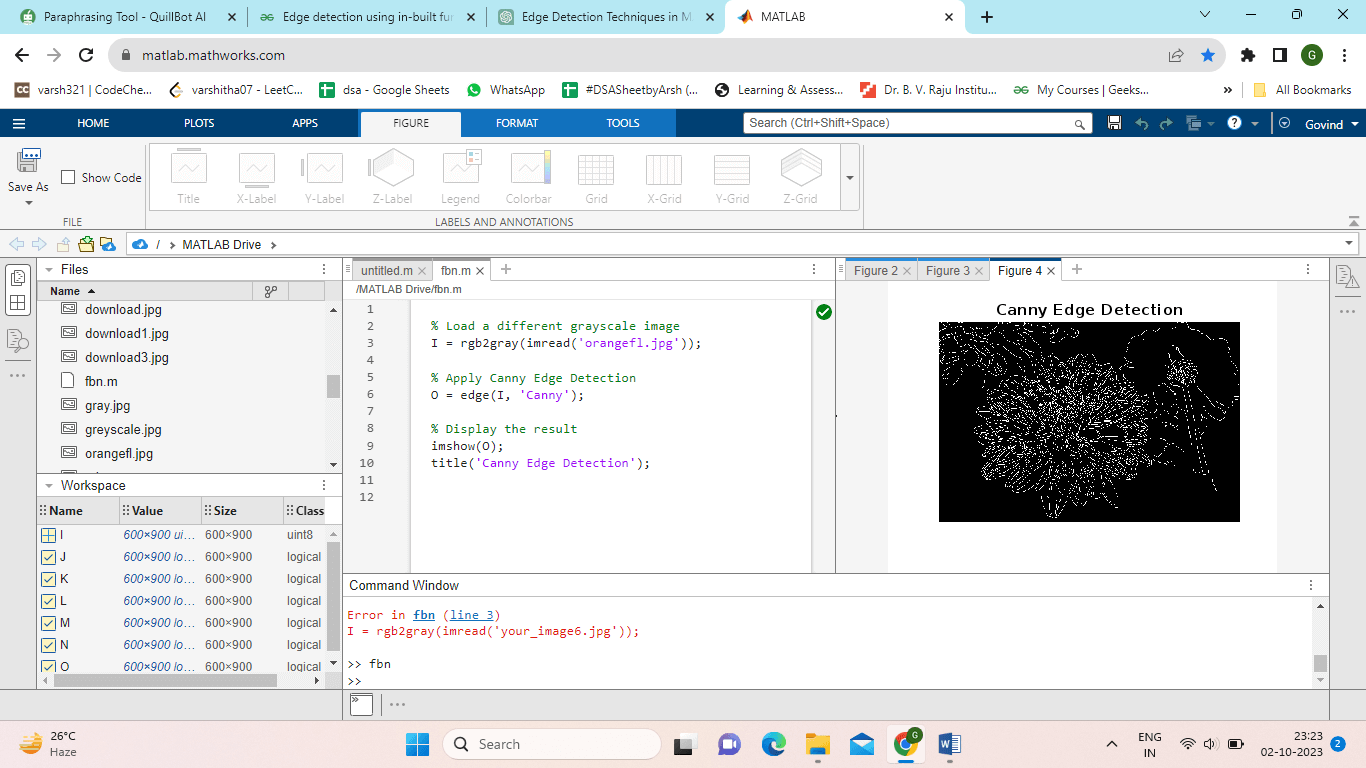 detection method has benefits and might be better suited for particular applications or types of photos.
• MATLAB offers these functions to allow users to select the most suitable approach based on their particular requirements for image processing.
• The type of edges you wish to detect, the intended trade-off between sensitivity and accuracy, and image noise all play a role in deciding which edge detector to utilize.

Examples:

Example:

Output:

The image is loaded into the application, which then uses the Canny edge detection technique to display the edge-detected result alongside the original image in a figure window.

By changing the set(gcf, 'Position', [100, 100, 800, 400]) line, you can change the figure window size as necessary.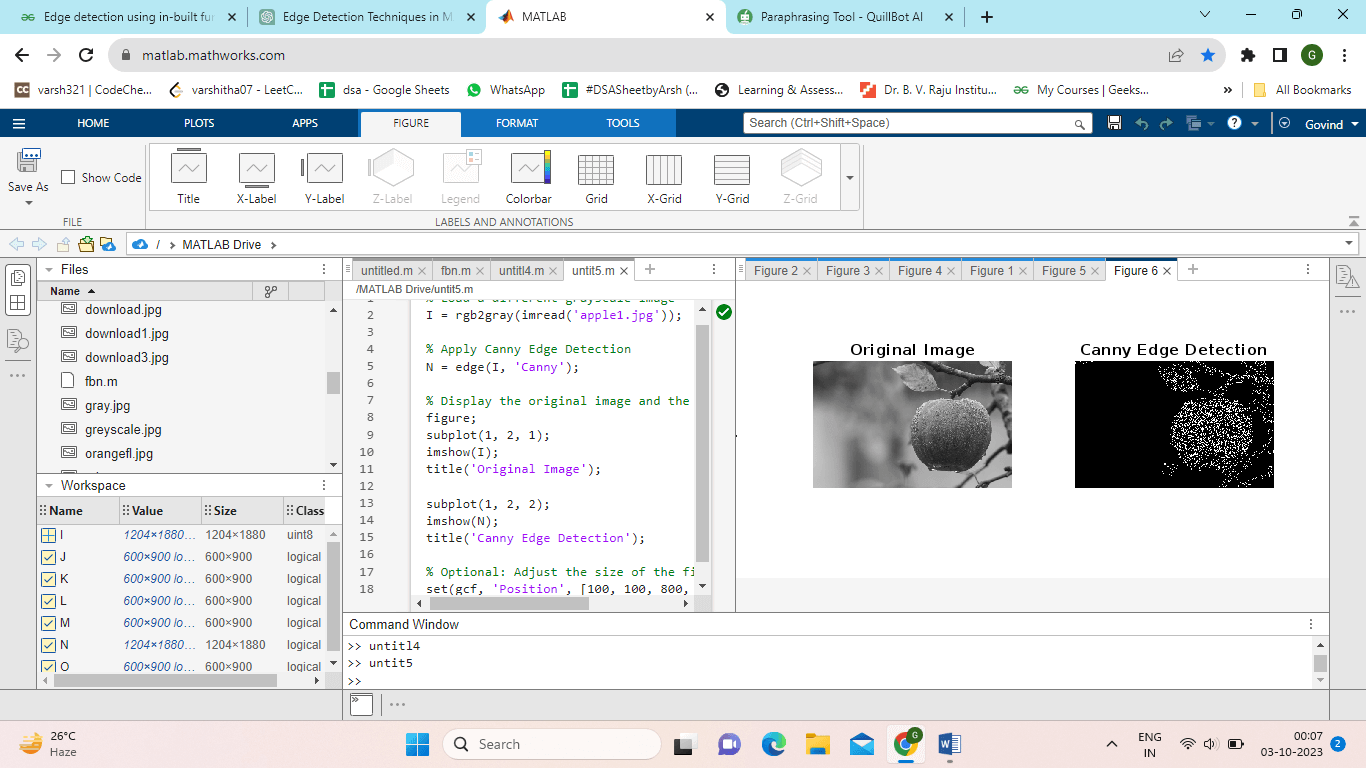

Implementations:

Various edge detection techniques on a grayscale image in MATLAB.

Explanation:

• Using the imshow function, Subplot (2, 4, 1) shows the original grayscale image. Using the title function, the title 'Original Image' is added.
• Sobel Edge identification: The outcome of Sobel edge identification is shown in Subplot (2, 4, 2). The Sobel filter uses the edge function, and imshow displays the resulting binary image. 'Sobel' is added to the title.
• Prewitt Edge Detection: Prewitt edge detection uses the Prewitt filter and is similar to the Sobel method in that it displays the results in Subplots (2, 4, and 3).
• Roberts Edge Detection: The outcome of Roberts Edge Detection, a different edge detection method based on a particular filter, is shown in Subplots (2, 4, 4).
• Detection of Log Edges (subplot 5)
• Detection of zero-cross edges (subplot 6)
• Detection of Canny Edges (subplot 7)

The appropriate edge-detected image for each method is created using edge and shown using imshow. Each Subplot receives a title to specify the chosen approach.

Output: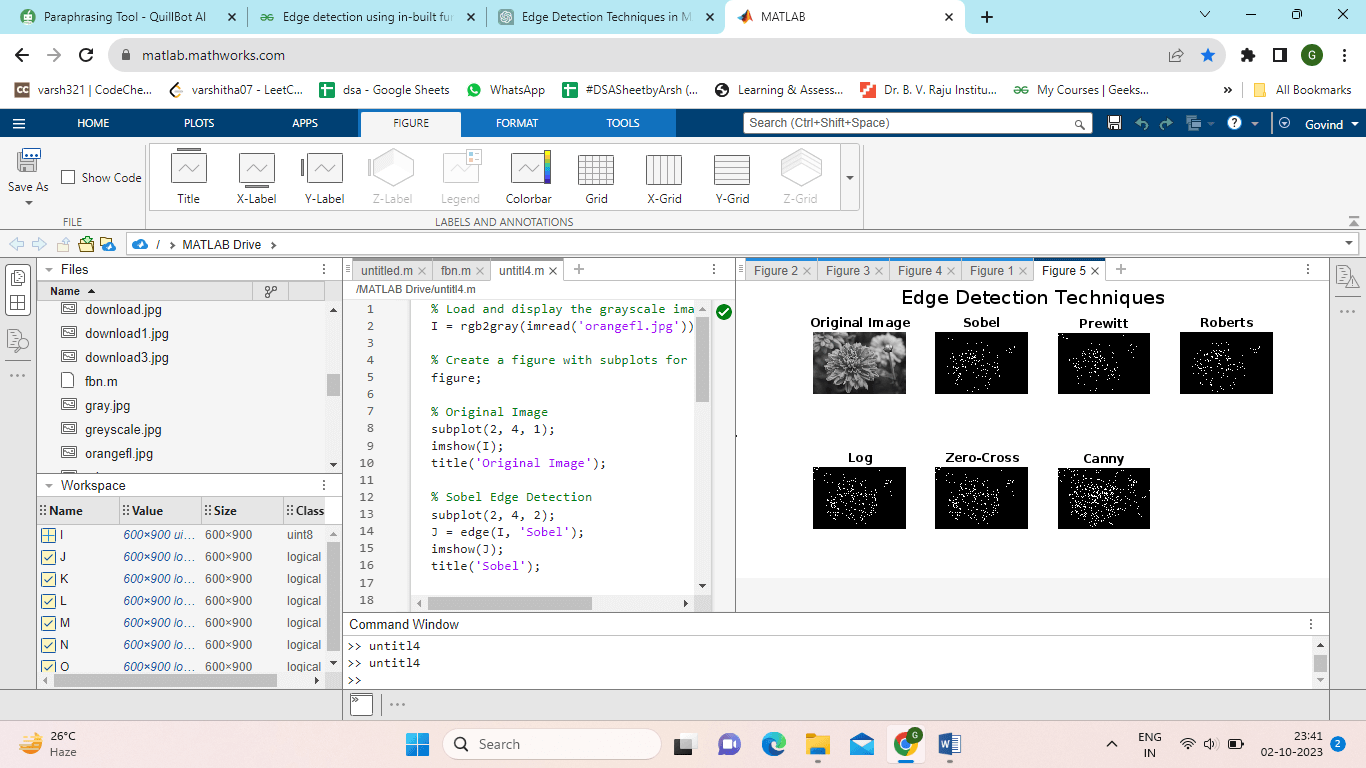

Advantages:

For a variety of applications, edge detection techniques in MATLAB and image processing in general offer significant benefits:

MATLAB is an effective tool for image processing tasks since it offers several edge detection algorithms.

• Researchers and engineers can extract useful information from photographs using these techniques, which are adaptable and widely utilized in various industries.

Feature Extraction: Edge detection aids in the identification and extraction of significant information from images, such as object borders, forms, and contours. For tasks like object detection and tracking, these qualities are essential.

Image Segmentation: Edge detection helps in image segmentation by helping to separate an image into useful parts or objects. This is crucial for activities like medical picture analysis, where it's important to identify various tissues or structures.

Object Detection: Edges might be a good place to start when finding objects. After edges are found, more analysis can be done to find and identify items in an image.

Boundary Detection: Edge detection is frequently used in computer vision and image analysis to find the borders of objects or regions of interest. The next processing stages make use of this data.

Noise Reduction: Edge detection can assist in reducing the impression of noise in an image. It can assist in separating genuine edges from noise by concentrating on sharp intensity fluctuations.

Image enhancement: By accentuating key details, edge enhancement techniques can be used to increase the visual appeal of an image and make it easier for humans to interpret.

Medical Imaging: For tasks like tumour diagnosis, organ segmentation, and blood vessel tracking, edge detection is frequently employed in medical image analysis.

Robotics and autonomous cars: Edge detection is important for detecting barriers and enabling safe navigation in robotics and driverless vehicles.

Quality Control: Edge detection can evaluate products for flaws or precisely measure dimensions in manufacturing and quality control applications.

Computer vision: Applications such as facial recognition, gesture identification, and augmented reality, where it is crucial to determine object borders and shapes, edge detection is key.

Artificial intelligence: To extract useful features from images for classification or regression problems, edge detection can be employed as a preprocessing step in machine learning and deep learning pipelines.

Enhanced Visualization: Edge-detected images can give a condensed and more comprehensible portrayal of complicated scenes, making it simpler for people to interpret and analyze visual information.

Disadvantages:

While edge detection methods in MATLAB and other image processing programs have many benefits, there are some drawbacks and difficulties as well:

Sensitivity to Noise: Edge detection techniques are susceptible to noise in the input image. Noisy pictures can result in missing edges (not identifying actual edges) or false positives (detecting edges that do not exist).

Parameter Tuning: Adjusting parameters, such as threshold levels, kernel sizes, or filter types, is necessary for many edge detection techniques. Iterative and time-consuming processes can be involved in choosing acceptable parameter values.

Edge Fragmentation: Edge detection algorithms may yield fragmented or broken edges in textured or complicated areas of an image, making it difficult to depict the true object boundaries precisely.

Missing Weak Edges: In some situations, weak or faint edges that could be critical to find may go undetected by some edge detection techniques.

False Positives and False Negatives: Edge detection can result in false positives (detecting edges where none exist) and false negatives (missing actual edges), depending on the technique and parameter selection.

Dependence on Image Quality: The performance of edge detection algorithms can be strongly impacted by the quality of the input image, including elements like resolution and lighting conditions.

Cost of Computing: Some edge detection techniques can be computationally expensive and may not be appropriate for real-time applications, particularly those that involve convolution with huge filters or sophisticated mathematical computations.

Trade-off Between Specification and Sensitivity: Increased sensitivity (the ability to detect more edges) can frequently result in decreased specificity (the ability to produce more false positives), and vice versa. Finding the ideal balance can be difficult.

Edge Width Variation: Since edges produced by edge detection methods frequently have different widths, it might not be easy to describe objects with reliable boundaries.

Ambiguity in Orientation: While edge detection normally reports edge locations, it may sometimes be unclear how the edges are oriented or if they signify abrupt or gradual changes in intensity.

Over-Enhancement: Some edge enhancement methods can increase noise, resulting in over-enhancing and making the image harder to interpret.

Difficulty with Textured Images: Textured images can be challenging for edge detection algorithms because they can result in many false edges when they include repetitive patterns or small features.

Limited in 3D and Multispectral Images: Edge detection is primarily intended for 2D grayscale photos and may only easily expand to 3D or multispectral data with modification.

Not Suitable for All Tasks: Edge detection is beneficial in various applications, although there might be better options for some image processing tasks, such as image denoising or colour correction.

It's crucial to select the edge detection method most suited for your application, thoroughly preprocess your photos to remove noise and fine-tune the settings to get the required results to handle these drawbacks.

• Edge detection can also be more accurate and robust by combining it with other image-processing methods and machine-learning strategies.