Summation in MATLAB

Introduction

Summation is one of the many mathematical operations that MATLAB, a popular programming language for technical and numerical computing, fully supports. Calculating the entire sum of a set of numbers and the accumulation of values throughout a sequence is known as summation, and it is a basic mathematical process. With a variety of built-in functions and tools in MATLAB, summation may be used for arrays, series, and even continuous functions.

• The fundamentals of evaluating series, obtaining definite integrals, computing cumulative sums, and summing arrays will all be covered. We will also discuss how to use optional arguments in the summation functions to fine-tune calculation control.

Summation notation

Summation notation is a concise and effective mathematical representation used to indicate the sum of a series of words. It is commonly represented by the symbol ∑, the upper-case Greek letter sigma. It is frequently used to concisely explain repeated addition processes in the sciences, engineering, and mathematics. The notation is made up of a number of essential elements, each of which is vital in specifying the parameters of the summation.

The Summation Sign (∑): The central symbol of the summation notation, the symbol ∑ resembles an uppercase Greek letter sigma. It indicates that a sequence's components need to be added up. The requirements for the summation variables are stated alongside the components to be summed to the right of the ∑ sign.

The Variables of Summation, or Index (i): The variable over which the summation is carried out is denoted by the Index, which is frequently written as "i," "j," or "k." The Index is displayed beneath the ∑ sign. It acts as a stand-in for the values of the upcoming elements. The lower and upper bounds of the summing define the Index's range.

The Summation's Lower Limit (Starting Point): This is the Index's starting value or the point at which the summing begins. It indicates the index value at which the summing starts.

The Summation's Upper Limit (Stopping Point): This is the maximum value that the Index can reach and indicates the end of the summing.

The summing is done for every index value, inclusively ranging from the lower to the upper limit.

• These elements are joined to create an expression in summation notation that concisely expresses the total of a series of terms across a given range.
• Numerous mathematical operations, such as the summation of arithmetic and geometric sequences, series, and other mathematical functions, can be represented by the notation.

Summation notation can be used to express the sum of the first n natural integers, for instance, as follows:

With 'i' serving as the index variable, this representation shows the total of all the integers from 1 to n, inclusive.

Similarly, we can express the sum of squares for the first n natural integers as follows:

In this case, the symbol represents the sum of squares of the numbers from 1 to n, where 'i' is the index variable that has values between 1 and n.

• It is essential to master the elements of summation notation in order to represent and understand mathematical operations and series effectively.
• It offers a concise and uniform representation of intricate mathematical relationships and concepts, facilitating more understandable communication and analysis across a range of scientific and academic disciplines.

Symposium:

In MATLAB, a symsum function is an effective tool for symbolically evaluating sums. Because it allows users to do symbolic expression summation, it is particularly helpful when working with intricate mathematical sequences and series.

• The function calculates the sum of an expression across a specified range with respect to a supplied symbolic variable.
• In mathematical calculations, physics, engineering, and other scientific applications where symbolic manipulation is required, the system function is frequently utilized.

S = symsum(s, i, a, b)

Below is a thorough explanation of every part of the system function:

S: The symbolic output, or outcome, of the symbolic summing is this. It symbolizes the given expression's symbolic sum over the designated range.

s: The symbolic expression or function that has to be summed is represented by this parameter. It may take the form of a straightforward phrase or a more intricate mathematical operation with symbolic variables.

i: This stands for the summation index or symbolic variable. As the sum moves over its range, it is the variable that changes.

A and b: These represent the summation's lower and upper bounds, respectively. Throughout the summing process, they specify the range over which the symbolic variable will fluctuate.

When assessing a variety of mathematical series, such as arithmetic, geometric, and more intricate infinite series, the symsum function comes in handy. It helps users to determine closed-form solutions for a variety of summations that are difficult to compute by hand. By utilizing MATLAB's symbolic math features, this function offers a practical method for managing symbolic expressions and calculations inside the MATLAB environment.

Summation of Arrays

Finding the sum of the elements in an array in MATLAB is a simple but crucial operation. The main tool for doing this is the sum function. It enables you to calculate the total of each element in an array or along a certain multidimensional array dimension.

Let A be an array whose elements are [5 6 7 8 9].

You may use the sum function in the following way to obtain the sum of all the entries in this array:

Output:

Here, the array A's members are added together using the sum function, yielding a total sum of 35. In MATLAB, more intricate summing jobs are built upon this fundamental technique.

Cumulative Sum

Moreover, MATLAB offers a handy method for calculating the cumulative sum of elements in an array by utilizing the cumsum function. By using this method, a new array is created, each element of which is the total of all the elements in the original array up to that point.

Consider the array A, which consists of the items [1 2 3 4 5].

You may find the cumulative sum of the items as follows by using the cumsum function:

Output: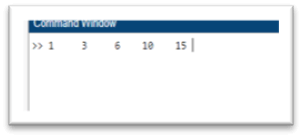

In this case, the array [1 3 6 10 15] is produced by adding the cumulative total of the components [1 2 3 4 5], where each element represents the sum of the corresponding elements in the original array up to that position.

Definite Integral

The integral function in MATLAB is used to calculate the definite integrals of functions over a given interval. With the help of this function, users can do numerical integration to determine the cumulative value of a continuous function within a particular range or the area under a curve. Calculus's definite integral is a basic idea, and MATLAB's integral function makes it easy to compute these integrals numerically for a variety of functions.

The integral function's general syntax is as follows:

Assume, for instance, that you wish to compute the definite integral of the function f(x)=x*2 and that you have a function.

Below is a thorough explanation of every element that makes up the integral function:

Q: The definite integral's numerical value is represented by this. It gives the area under the curve, or cumulative value, of the given function across the interval [a, b].

fun: This is the feature that has to be included. It can be defined with the @(x) notation, as a function handle, or inline.

a and b: The parameters a and b delineate the definite integral's lower and upper bounds, respectively. They define the period that the integration is to be carried out.

The integral function can be applied as follows:

Output: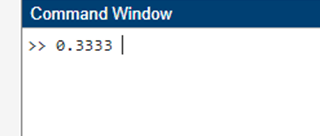

The definite integral of the function f(x)=2x across the range [0, 1] is computed in this example using the integral function, yielding the numerical value 1/3, or around 0.3333. This illustrates how the integral function may be used to carry out numerical integration for a variety of function kinds and provide precise, definite integral results in MATLAB.

Summation with optional Argument

MATLAB's sum function has a number of optional arguments that offer more versatility when working with arrays and executing particular summing operations. These parameters include the array's infinities and NaN (Not-a-Number) values, as well as the dimension along which the summing is carried out. Summation along a Specific Dimension

In multidimensional array operations, it could be necessary to calculate the sum along a certain dimension. You can designate the dimension along which the summing should be carried out using the sum function.

C = [1 2 3; 4 5 6; 7 8 9];

The following syntax can be used to find the sum of elements along the rows (dimension 1):

Output: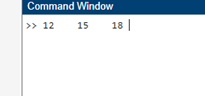

Handling Infinities and NaN

Options are available in MATLAB for managing infinities and NaN values during summation processes. You can choose to include or exclude NaN values from the summing with the 'include' options. In a similar vein, infinities are handled differently during summing depending on the 'omitinf' and 'includeinf' options.

Assume you have an array D that contains values for NaN and infinity.

To compute the sum while ignoring NaN values, you can use the 'omitan' Argument as follows: sum_without_nan = sum(D, 'omitnan');

Output:

7

Here, the sum function calculates the sum of elements in the array D, excluding the NaN value, resulting in the sum of 7.