MATLAB Indexing

Introduction

A key component of data manipulation and analysis in MATLAB is indexing, which enables users to access and work with certain parts of arrays or matrices. MATLAB facilitates complex data processing processes and improves the overall efficiency of numerical computations by providing users with the ability to efficiently retrieve, change, and edit data pieces within arrays through its extensive indexing features. This thorough manual explores the complexities of MATLAB indexing, going into great detail about its several facets, methods, and uses.

MATLAB Indexing Knowledge of Arrays and Matrices

Arrays and matrices are the basic data structures used in MATLAB for handling and storing numerical data. One-dimensional, two-dimensional, or multidimensional arrays can be created, depending on how complicated the data is. Comprehending the structure of arrays and matrices is essential to grasping the notion of indexing since it serves as the foundation for gaining access to and modifying data items inside these structures.

What is Indexing?

The technique of accessing particular elements or subsets of elements within arrays or matrices is known as "MATLAB indexing."

• It makes locating and modifying data pieces easier for users, which helps with a variety of data analysis and modification activities.
• Users can access individual items, rows, columns, or certain subsets of data by utilizing various indexing techniques, which facilitates intricate data processing procedures and mathematical computations.

The Value of MATLAB Indexing

In order to improve the efficacy and efficiency of MATLAB data manipulation and analysis, indexing is essential.

• Indexing makes a variety of numerical operations, data processing tasks, and statistical analysis easier by allowing users to access and change individual data items within arrays and matrices.
• Effective indexing strategies make MATLAB an essential tool for data analysis and scientific computing by improving code readability, increasing computational efficiency, and streamlining data processing.

Simple MATLAB Indexing Techniques

Reaching Specific Components

Finding specific elements within an array or matrix is one of the core indexing methods in MATLAB. If a user wants to access a certain element, they can specify the row and column index. For instance, the indexing operation would be A(2, 3) to access the elements in the second row and third column of a matrix A. The foundation for more intricate MATLAB indexing operations is this straightforward method.

Dividing Matrices and Arrays

Using slicing procedures, MATLAB users can extract particular portions of data from arrays or matrices. If users want to extract a subset of the data, they can provide ranges of rows or columns. For example, the indexing operation A(1:3) would be used to extract the first three items of vector A. Similar to this, users can provide the range of indices in a matrix to extract a subset of rows or columns. For example, A(2:4, 1:3) extracts rows 2 to 4 and columns 1 to 3.

Reasonable Indexing

Users can extract data elements based on particular logical conditions by using logical indexing. In order to extract the necessary elements, users can build a logical array with constraints depending on the original array's elements and then use this logical array as an index. For instance, users can construct a logical array with the name A > threshold and use it as an index to retrieve the elements matching the condition, as in A(A > threshold), to extract elements from vector A that are greater than a given value.

Indexing Linearly

By treating an array like a one-dimensional vector, linear indexing enables users to retrieve members of the array using a single index. MATLAB facilitates efficient data access and manipulation by internally converting the linear index to the appropriate row and column indices. For instance, the linear indexing operation would be A(5) to retrieve the fifth member of a 3x3 matrix A.

Lists separated by commas

Comma-separated lists can be used in MATLAB to index multidimensional arrays. In multidimensional arrays, users can access specific elements or subsets of elements by specifying the indices for each dimension, separated by commas. To retrieve a particular element from a 3D array A, for example, the indexing operation would be A(2, 3, 1) to retrieve the element at the array's second row, third column, and first page.

Advanced MATLAB Indexing Methods

Differential Dimension Indexing

Multidimensional indexing in MATLAB makes it possible to retrieve elements from arrays with more than two dimensions. To access particular elements or subsets of elements from multidimensional arrays, users can specify the indices for each dimension, separated by the relevant dimensions. For example, users can access the element at the second row, third column, first page, and fourth depth of a 4D array A by using the indexing operation A(2, 3, 1, 4).

Indexing with Conditions

In MATLAB, conditional indexing entails the extraction of data items according to intricate conditional expressions or logical procedures. Logical operators like AND (&), OR (|), and NOT (~) allow users to specify complex criteria for data extraction. This sophisticated indexing method helps with complex data analysis and manipulation activities by filtering and extracting certain data pieces based on complex criteria.

Using Functions for Indexing

With indexing operations, MATLAB users can apply functions directly to arrays or matrices, allowing for more effective data processing and manipulation. Users can execute a variety of mathematical operations or data transformations on individual items or subsets of elements within arrays by using built-in or custom functions with indexing operations. This feature increases MATLAB's adaptability to difficult data processing and analysis jobs by enabling users to implement complex algorithms and data manipulation procedures easily.

Indexing Using Unidentified Functions

Quick and effective data processing is made possible by MATLAB's anonymous functions, which let users construct and use short, anonymous functions immediately within indexing procedures. To streamline complex data manipulation activities and improve MATLAB's overall computing performance, users can develop anonymous functions that carry out specific operations on data components and include them directly into indexing procedures.

Let's look at a few real-world examples to illustrate various indexing strategies and their uses.

Example 1: Fundamental Indexing Functions

Output:

This example shows how to extract individual elements and subsets of elements from a 3x3 matrix using simple indexing methods. The value of the element in the second row and third column is stored in the variable element. The variable subset1 represents the first two rows and columns of the matrix, while the third column of matrix A is stored in subset2.

Example 2: Logical Indexing

Output:

This MATLAB example shows how to use logical indexing. We build a logical array called logical_indices based on the premise that the members of the sample vector B, which contains numerical values, are bigger than the threshold value. Lastly, the items of B that meet the logical requirement are kept in the variable subset3.

Example 3: Multidimensional Indexing

Output: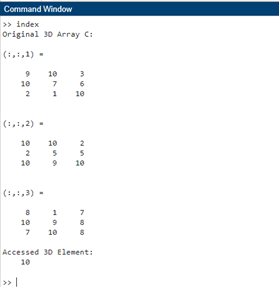

Using random integer values, we generate a 3x3x3 3D array C in this example. In order to illustrate multidimensional indexing in MATLAB, the variable element_3d represents the element at the second row, first column, and third page of the 3D array.

Applications of MATLAB Indexing

Image Processing

MATLAB indexing finds extensive applications in image processing tasks, enabling users to extract specific pixels, regions of interest, or features from images for analysis and manipulation. By leveraging various indexing techniques, users can perform tasks such as image segmentation, feature extraction, and image enhancement, facilitating advanced image processing operations and analysis.

Signal Processing

In signal processing applications, MATLAB indexing is instrumental in extracting and processing specific segments or components of signals, enabling users to perform tasks such as signal filtering, noise removal, and signal analysis. By utilizing indexing techniques, users can extract signal components of interest, apply digital filters, and perform spectral analysis, facilitating comprehensive signal processing operations and enhancing the accuracy of data analysis.

Data Analysis and Visualization

MATLAB indexing facilitates efficient data analysis and visualization, allowing users to extract, process, and visualize specific data subsets or components for detailed analysis and interpretation. By employing indexing techniques, users can extract data subsets based on specific criteria, perform statistical analysis, and generate informative visualizations, thereby enhancing the interpretability and insight-generation capabilities of data analysis tasks.

Numerical Computations and Simulations

In numerical computations and simulations, MATLAB indexing enables users to extract and manipulate specific elements or subsets of data for performing complex mathematical computations and simulations. By leveraging advanced indexing techniques, users can access data elements for numerical integration, solve differential equations, and simulate complex systems, facilitating comprehensive numerical computations and simulations for diverse scientific and engineering applications.

Machine Learning and Deep Learning

MATLAB indexing plays a critical role in machine learning and deep learning applications, enabling users to preprocess and manipulate data for training and testing machine learning models. By employing indexing techniques, users can preprocess data, extract features, and prepare data sets for training machine learning models, facilitating efficiency.