Sparse Arrays in MATLABWhen an ordinary array is declared, MATLAB creates a memory location for every element in the array. For example, the function a = eye (10) creates 100 elements arranged as a 10 x 10 structure. In this array, 90 of those elements are zero! This matrix requires 100 elements, but only 10 of them contain nonzero data. This is an example of a sparse array or sparse matrix. A sparse matrix is a large matrix in which the vast majority of the elements are zero. 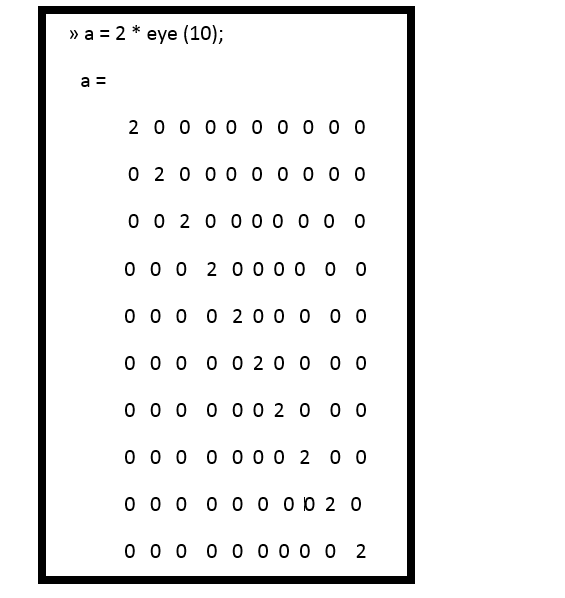
Now suppose that we create another 10 x 10 matrix b defined as follows: 
If these two matrices are multiplied together, the result is 
Sparse AttributeMATLAB has a particular version of the double data type that is designed to work with sparse arrays. In this particular version of the double data type, only the nonzero elements of an array are allocated memory locations, and the array is said to have the "sparse" attribute. An array with the sparse attribute saves three values for each nonzero element: the value of the element itself and the row and column numbers where the element is located. Even though three values must be saved for each nonzero element, this approach is much more memory efficient than allocating full arrays if a matrix has only a few nonzero elements. To illustrate the use of sparse matrices, we will create a 10 x 10 identity matrix: 
If this matrix is converted to a sparse matrix using function sparse, the results are 
If we examine arrays a and as with the whos command, the results are The a array occupies 800 bytes because there are 100 elements with 8 bytes of storage each. The as array occupies 164 bytes because there are 10 nonzero elements with 8 bytes of storage each, plus 20 array indices occupying 4 bytes each, and 4 bytes of overhead. Note that the sparse array occupies much less memory than the full array. The function issparse can be used to determine whether or not a given array is sparse. If an array is sparse, then issparse (array) returns true (1). The power of the sparse data type can be seen by considering a 1000 x 1000 matrix z with an average of 4 nonzero elements per row. If this matrix is stored as a full matrix, it will require 8,000,000 bytes of space. On the other hand, if it is converted to a sparse matrix, the memory usage will drop dramatically. Generating Sparse MatricesMATLAB can generate sparse matrices by converting a full matrix into a sparse matrix with the sparse function or by directly making sparse matrices with the MATLAB functions speye, sprand, and sprandn, which are the sparse equivalents of the eye, rand, and randn. The expression b = full (a) converts the sparse matrix into a full matrix. Working with Sparse MatricesOnce a matrix has been made sparse, individual elements can be added to it or deleted from it using simple assignment statements. For example, the following statement generates a 4 x 4 sparse matrix and then adds another nonzero element to it: Sparse Matrix FunctionsThis table display some of the functions most generally used when working with sparse matrices.
Next TopicMATLAB M-Files
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









