Bayes Theorem in Machine learningMachine Learning is one of the most emerging technology of Artificial Intelligence. We are living in the 21th century which is completely driven by new technologies and gadgets in which some are yet to be used and few are on its full potential. Similarly, Machine Learning is also a technology that is still in its developing phase. There are lots of concepts that make machine learning a better technology such as supervised learning, unsupervised learning, reinforcement learning, perceptron models, Neural networks, etc. In this article "Bayes Theorem in Machine Learning", we will discuss another most important concept of Machine Learning theorem i.e., Bayes Theorem. But before starting this topic you should have essential understanding of this theorem such as what exactly is Bayes theorem, why it is used in Machine Learning, examples of Bayes theorem in Machine Learning and much more. So, let's start the brief introduction of Bayes theorem. 
Introduction to Bayes Theorem in Machine LearningBayes theorem is given by an English statistician, philosopher, and Presbyterian minister named Mr. Thomas Bayes in 17th century. Bayes provides their thoughts in decision theory which is extensively used in important mathematics concepts as Probability. Bayes theorem is also widely used in Machine Learning where we need to predict classes precisely and accurately. An important concept of Bayes theorem named Bayesian method is used to calculate conditional probability in Machine Learning application that includes classification tasks. Further, a simplified version of Bayes theorem (Naïve Bayes classification) is also used to reduce computation time and average cost of the projects. Bayes theorem is also known with some other name such as Bayes rule or Bayes Law. Bayes theorem helps to determine the probability of an event with random knowledge. It is used to calculate the probability of occurring one event while other one already occurred. It is a best method to relate the condition probability and marginal probability. In simple words, we can say that Bayes theorem helps to contribute more accurate results. Bayes Theorem is used to estimate the precision of values and provides a method for calculating the conditional probability. However, it is hypocritically a simple calculation but it is used to easily calculate the conditional probability of events where intuition often fails. Some of the data scientist assumes that Bayes theorem is most widely used in financial industries but it is not like that. Other than financial, Bayes theorem is also extensively applied in health and medical, research and survey industry, aeronautical sector, etc. What is Bayes Theorem?Bayes theorem is one of the most popular machine learning concepts that helps to calculate the probability of occurring one event with uncertain knowledge while other one has already occurred. Bayes' theorem can be derived using product rule and conditional probability of event X with known event Y:
Mathematically, Bayes theorem can be expressed by combining both equations on right hand side. We will get: 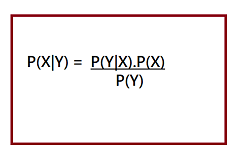
Here, both events X and Y are independent events which means probability of outcome of both events does not depends one another. The above equation is called as Bayes Rule or Bayes Theorem.
Hence, Bayes Theorem can be written as: posterior = likelihood * prior / evidence Prerequisites for Bayes TheoremWhile studying the Bayes theorem, we need to understand few important concepts. These are as follows: 1. Experiment An experiment is defined as the planned operation carried out under controlled condition such as tossing a coin, drawing a card and rolling a dice, etc. 2. Sample Space During an experiment what we get as a result is called as possible outcomes and the set of all possible outcome of an event is known as sample space. For example, if we are rolling a dice, sample space will be: S1 = {1, 2, 3, 4, 5, 6} Similarly, if our experiment is related to toss a coin and recording its outcomes, then sample space will be: S2 = {Head, Tail} 3. Event Event is defined as subset of sample space in an experiment. Further, it is also called as set of outcomes. 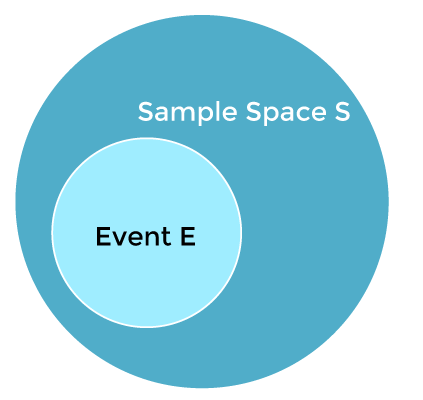
Assume in our experiment of rolling a dice, there are two event A and B such that; A = Event when an even number is obtained = {2, 4, 6} B = Event when a number is greater than 4 = {5, 6}
4. Random Variable: It is a real value function which helps mapping between sample space and a real line of an experiment. A random variable is taken on some random values and each value having some probability. However, it is neither random nor a variable but it behaves as a function which can either be discrete, continuous or combination of both. 5. Exhaustive Event: As per the name suggests, a set of events where at least one event occurs at a time, called exhaustive event of an experiment. Thus, two events A and B are said to be exhaustive if either A or B definitely occur at a time and both are mutually exclusive for e.g., while tossing a coin, either it will be a Head or may be a Tail. 6. Independent Event: Two events are said to be independent when occurrence of one event does not affect the occurrence of another event. In simple words we can say that the probability of outcome of both events does not depends one another. Mathematically, two events A and B are said to be independent if: P(A ∩ B) = P(AB) = P(A)*P(B) 7. Conditional Probability: Conditional probability is defined as the probability of an event A, given that another event B has already occurred (i.e. A conditional B). This is represented by P(A|B) and we can define it as: P(A|B) = P(A ∩ B) / P(B) 8. Marginal Probability: Marginal probability is defined as the probability of an event A occurring independent of any other event B. Further, it is considered as the probability of evidence under any consideration. P(A) = P(A|B)*P(B) + P(A|~B)*P(~B) 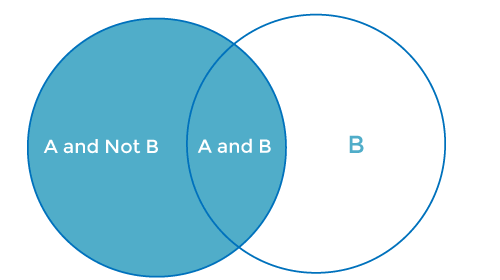
Here ~B represents the event that B does not occur. How to apply Bayes Theorem or Bayes rule in Machine Learning?Bayes theorem helps us to calculate the single term P(B|A) in terms of P(A|B), P(B), and P(A). This rule is very helpful in such scenarios where we have a good probability of P(A|B), P(B), and P(A) and need to determine the fourth term. Naïve Bayes classifier is one of the simplest applications of Bayes theorem which is used in classification algorithms to isolate data as per accuracy, speed and classes. Let's understand the use of Bayes theorem in machine learning with below example. Suppose, we have a vector A with I attributes. It means A = A1, A2, A3, A4……………Ai Further, we have n classes represented as C1, C2, C3, C4…………Cn. These are two conditions given to us, and our classifier that works on Machine Language has to predict A and the first thing that our classifier has to choose will be the best possible class. So, with the help of Bayes theorem, we can write it as: P(Ci/A)= [ P(A/Ci) * P(Ci)] / P(A) Here; P(A) is the condition-independent entity. P(A) will remain constant throughout the class means it does not change its value with respect to change in class. To maximize the P(Ci/A), we have to maximize the value of term P(A/Ci) * P(Ci). With n number classes on the probability list let's assume that the possibility of any class being the right answer is equally likely. Considering this factor, we can say that: P(C1)=P(C2)-P(C3)=P(C4)=…..=P(Cn). This process helps us to reduce the computation cost as well as time. This is how Bayes theorem plays a significant role in Machine Learning and Naïve Bayes theorem has simplified the conditional probability tasks without affecting the precision. Hence, we can conclude that: P(Ai/C)= P(A1/C)* P(A2/C)* P(A3/C)*……*P(An/C) Hence, by using Bayes theorem in Machine Learning we can easily describe the possibilities of smaller events. What is Naïve Bayes Classifier in Machine LearningNaïve Bayes theorem is also a supervised algorithm, which is based on Bayes theorem and used to solve classification problems. It is one of the most simple and effective classification algorithms in Machine Learning which enables us to build various ML models for quick predictions. It is a probabilistic classifier that means it predicts on the basis of probability of an object. Some popular Naïve Bayes algorithms are spam filtration, Sentimental analysis, and classifying articles. Advantages of Naïve Bayes Classifier in Machine Learning:
Disadvantages of Naïve Bayes Classifier in Machine Learning:The main disadvantage of using Naïve Bayes classifier algorithms is, it limits the assumption of independent predictors because it implicitly assumes that all attributes are independent or unrelated but in real life it is not feasible to get mutually independent attributes. ConclusionThough, we are living in technology world where everything is based on various new technologies that are in developing phase but still these are incomplete in absence of already available classical theorems and algorithms. Bayes theorem is also most popular example that is used in Machine Learning. Bayes theorem has so many applications in Machine Learning. In classification related problems, it is one of the most preferred methods than all other algorithm. Hence, we can say that Machine Learning is highly dependent on Bayes theorem. In this article, we have discussed about Bayes theorem, how can we apply Bayes theorem in Machine Learning, Naïve Bayes Classifier, etc.
Next TopicPerceptron in Machine Learning
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share