Optimization using Hopfield NetworkOptimization is the process of making something such as the design, environment, resource, and system as efficient as possible by utilizing a resemblance of the cost function and the energy function. One such type of neural network is called a Hopfield network, which is composed of a single layer that contains at least one of the fully connected recurrent neural networks. It can be utilized to optimize. Things to keep in mind when using the Hopfield network to optimize -
Travelling Salesman ProblemFinding the most efficient route the salesperson takes is among the computational challenges that can be improved by using Hopfield neural networks. Basic Concept of TSPThe Travelling Salesman Problem the TSP is a classic optimization problem where salespeople have to travel through a number of cities connected to one another and keep the costs. The distance travelled is at a minimum. For instance, a salesperson must travel through a set of four cities, A, B, C, and D. The objective is to determine the most efficient circular route, A-B-C-D, in order to reduce the cost, which includes the cost of traveling from city D to the next one city A. 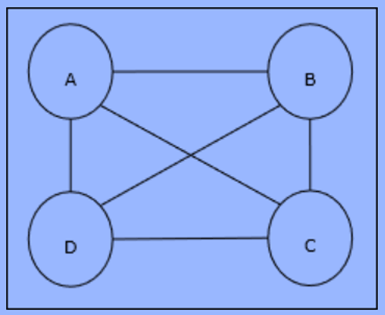
Matrix RepresentationEach tour of the TSP for n cities could be described in a matrix n x N which's ith row identifies the location of each city. The matrix M, for four cities, A, B, C, and D, could be expressed in the following manner: as follows: 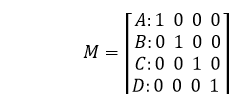
Solution by Hopfield NetworkWhen analysing the solution to the TSP using a Hopfield network, each node in the network is linked to a specific element of the matrix. Energy Function CalculationIn order to be the optimal solution for optimal results, the energy function should be as low as possible. Based on the above constraints, we are able to determine the function of energy using the following formula: -- Constraint-I The first constraint, on that basis, we calculate the energy function, is that one component must be at least 1 in every row on the matrix M and all other elements in each row have not to be greater than the value 0 because each city may occur in only one location within the TSP tour. This constraint can be mathematically expressed as follows: 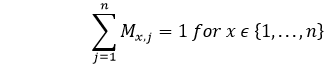
Based on the above constraint, now, we will minimize the energy function, that will contain the term proportional to: 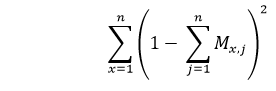
Constraint-II As we all know, in TSP, one city may be found at any location within the tour. Therefore, in every column of M, each element has to be equal to 1, and the other elements have to be equal to the value 0. This restriction can mathematically be expressed as follows: 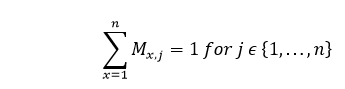
Based on the above constraint, now, we will minimize the energy function, that will contain the term proportional to: 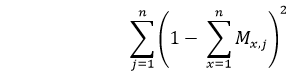
Cost Function CalculationLet's say that a square matrix ( n x n) that is represented with C is the cost matrix for TSP for the n cities in which there is a value of n greater than. Here are some of the parameters to consider when calculating the cost function
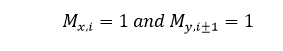
We know that within the Matrix, it is possible to determine the value of output for each node could be one or zero, so for each city pair A and B, we can include the following words for the power function. 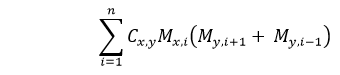
Based on the cost function above, along with the value for constraint end value of the energy-related calculation function, E can be described as follows: 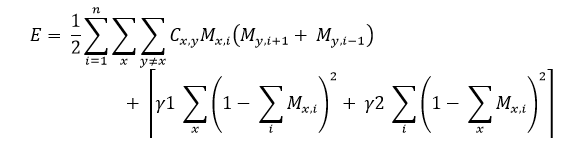
Here, γ1 and γ2 are two weighing constants.
Next TopicData Leakage in Machine Learning
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









