EM Algorithm in Machine Learning

The EM algorithm is considered a latent variable model to find the local maximum likelihood parameters of a statistical model, proposed by Arthur Dempster, Nan Laird, and Donald Rubin in 1977. The EM (Expectation-Maximization) algorithm is one of the most commonly used terms in machine learning to obtain maximum likelihood estimates of variables that are sometimes observable and sometimes not. However, it is also applicable to unobserved data or sometimes called latent. It has various real-world applications in statistics, including obtaining the mode of the posterior marginal distribution of parameters in machine learning and data mining applications.

In most real-life applications of machine learning, it is found that several relevant learning features are available, but very few of them are observable, and the rest are unobservable. If the variables are observable, then it can predict the value using instances. On the other hand, the variables which are latent or directly not observable, for such variables Expectation-Maximization (EM) algorithm plays a vital role to predict the value with the condition that the general form of probability distribution governing those latent variables is known to us. In this topic, we will discuss a basic introduction to the EM algorithm, a flow chart of the EM algorithm, its applications, advantages, and disadvantages of EM algorithm, etc.

What is an EM algorithm?

The Expectation-Maximization (EM) algorithm is defined as the combination of various unsupervised machine learning algorithms, which is used to determine the local maximum likelihood estimates (MLE) or maximum a posteriori estimates (MAP) for unobservable variables in statistical models. Further, it is a technique to find maximum likelihood estimation when the latent variables are present. It is also referred to as the latent variable model.

A latent variable model consists of both observable and unobservable variables where observable can be predicted while unobserved are inferred from the observed variable. These unobservable variables are known as latent variables.

Key Points:

• It is known as the latent variable model to determine MLE and MAP parameters for latent variables.
• It is used to predict values of parameters in instances where data is missing or unobservable for learning, and this is done until convergence of the values occurs.

EM Algorithm

The EM algorithm is the combination of various unsupervised ML algorithms, such as the k-means clustering algorithm. Being an iterative approach, it consists of two modes. In the first mode, we estimate the missing or latent variables. Hence it is referred to as the Expectation/estimation step (E-step). Further, the other mode is used to optimize the parameters of the models so that it can explain the data more clearly. The second mode is known as the maximization-step or M-step.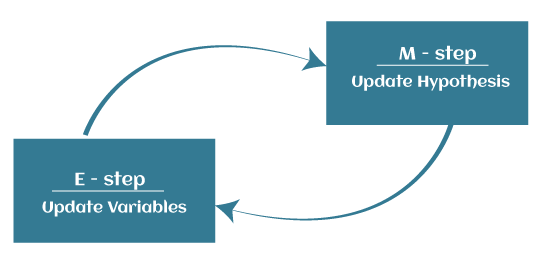

• Expectation step (E - step): It involves the estimation (guess) of all missing values in the dataset so that after completing this step, there should not be any missing value.
• Maximization step (M - step): This step involves the use of estimated data in the E-step and updating the parameters.
• Repeat E-step and M-step until the convergence of the values occurs.

The primary goal of the EM algorithm is to use the available observed data of the dataset to estimate the missing data of the latent variables and then use that data to update the values of the parameters in the M-step.

What is Convergence in the EM algorithm?

Convergence is defined as the specific situation in probability based on intuition, e.g., if there are two random variables that have very less difference in their probability, then they are known as converged. In other words, whenever the values of given variables are matched with each other, it is called convergence.

Steps in EM Algorithm

The EM algorithm is completed mainly in 4 steps, which include Initialization Step, Expectation Step, Maximization Step, and convergence Step. These steps are explained as follows: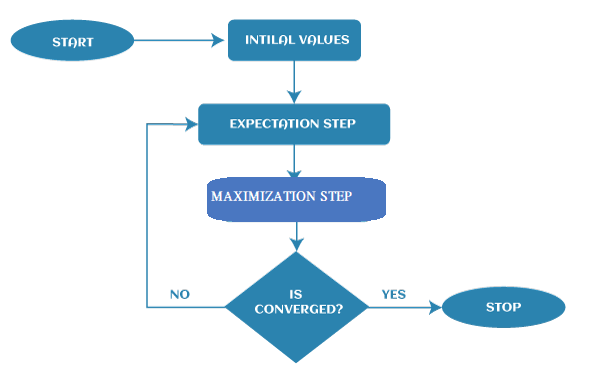

• 1^st Step: The very first step is to initialize the parameter values. Further, the system is provided with incomplete observed data with the assumption that data is obtained from a specific model.

• 2^nd Step: This step is known as Expectation or E-Step, which is used to estimate or guess the values of the missing or incomplete data using the observed data. Further, E-step primarily updates the variables.
• 3^rd Step: This step is known as Maximization or M-step, where we use complete data obtained from the 2^nd step to update the parameter values. Further, M-step primarily updates the hypothesis.
• 4^th step: The last step is to check if the values of latent variables are converging or not. If it gets "yes", then stop the process; else, repeat the process from step 2 until the convergence occurs.

Gaussian Mixture Model (GMM)

The Gaussian Mixture Model or GMM is defined as a mixture model that has a combination of the unspecified probability distribution function. Further, GMM also requires estimated statistics values such as mean and standard deviation or parameters. It is used to estimate the parameters of the probability distributions to best fit the density of a given training dataset. Although there are plenty of techniques available to estimate the parameter of the Gaussian Mixture Model (GMM), the Maximum Likelihood Estimation is one of the most popular techniques among them.

Let's understand a case where we have a dataset with multiple data points generated by two different processes. However, both processes contain a similar Gaussian probability distribution and combined data. Hence it is very difficult to discriminate which distribution a given point may belong to.

The processes used to generate the data point represent a latent variable or unobservable data. In such cases, the Estimation-Maximization algorithm is one of the best techniques which helps us to estimate the parameters of the gaussian distributions. In the EM algorithm, E-step estimates the expected value for each latent variable, whereas M-step helps in optimizing them significantly using the Maximum Likelihood Estimation (MLE). Further, this process is repeated until a good set of latent values, and a maximum likelihood is achieved that fits the data.

Applications of EM algorithm

The primary aim of the EM algorithm is to estimate the missing data in the latent variables through observed data in datasets. The EM algorithm or latent variable model has a broad range of real-life applications in machine learning. These are as follows:

• The EM algorithm is applicable in data clustering in machine learning.
• It is often used in computer vision and NLP (Natural language processing).
• It is used to estimate the value of the parameter in mixed models such as the Gaussian Mixture Modeland quantitative genetics.
• It is also used in psychometrics for estimating item parameters and latent abilities of item response theory models.
• It is also applicable in the medical and healthcare industry, such as in image reconstruction and structural engineering.
• It is used to determine the Gaussian density of a function.

Advantages of EM algorithm

• It is very easy to implement the first two basic steps of the EM algorithm in various machine learning problems, which are E-step and M- step.
• It is mostly guaranteed that likelihood will enhance after each iteration.
• It often generates a solution for the M-step in the closed form.

Disadvantages of EM algorithm

• The convergence of the EM algorithm is very slow.
• It can make convergence for the local optima only.
• It takes both forward and backward probability into consideration. It is opposite to that of numerical optimization, which takes only forward probabilities.

Conclusion

In real-world applications of machine learning, the expectation-maximization (EM) algorithm plays a significant role in determining the local maximum likelihood estimates (MLE) or maximum a posteriori estimates (MAP) for unobservable variables in statistical models. It is often used for the latent variables, i.e., to estimate the latent variables through observed data in datasets. It is generally completed in two important steps, i.e., the expectation step (E-step) and the Maximization step (M-Step), where E-step is used to estimate the missing data in datasets, and M-step is used to update the parameters after the complete data is generated in E-step. Further, the importance of the EM algorithm can be seen in various applications such as data clustering, natural language processing (NLP), computer vision, image reconstruction, structural engineering, etc.