Continuous Value Prediction

Topics

The file attached includes the following topics and sub-topics

1. Elements In Machine Learning

• Data
• Training data
• Features
• Algorithms
• Model evaluation
• Hyperparameter tuning
• Underfitting and overfitting
• Deployment
• Ethical considerations

2. Regression

• Various Regression
• Model assessment
• Assumptions
• Applications
• Regularization

3. Regression Types In Detail

• Simple linear Regression
  
  • Important formulas
  • Example Explanation
• Ridge Regression
  
  • Important formulas
  • Example Explanation
• Lasso Regression
  
  • Important formulas
  • Example Explanation
• Multiple Linear Regression
  
  • Important formulas
  • Example Explanation
• Polynomial Regression
  
  • Important formulas
  • Example Explanation
• Logistic Regression
  
  • Important formulas
  • Example Explanation

4. Conclusion

Now, let us Dive Deep into Every Topic

MachineLearning

Machine Learning is all about making a machine learn as humans do. There are many techniques involved which help us to train the model and work accordingly as required.

ElementsInMachineLearning

Here are some essential machine-learning ideas and elements:

1. Data:
   Algorithms of Machine learning mostly depend on data to learn and produce predictions. Both unstructured (such as text, graphics, or audio) and structured (such as tabular data) forms of this information are possible.
2. TrainingData:
   A labeled dataset is required to train a machine-learning model. This indicates that the data contains examples for which it is known the right responses or results. To generate predictions on fresh, unforeseen data, the model learns from this data.
3. Features:
   The specific pieces of data that the model uses to create predictions are referred to as features. The process of choosing and modifying pertinent characteristics from the data is known as feature engineering.
4. Algorithms:
   Different machine learning algorithms exist, each of which was created for a particular class of problems. These include, among others, reinforcement learning, unsupervised learning, and supervised learning.
   A model is trained on labeled data through supervised learning, which teaches it to anticipate outcomes based on input-output pairs. Decision trees, support vector machines, and neural networks are examples of common algorithms.
   Unsupervised learning utilizes unlabelled data and concentrates on finding structures or patterns in the data. Examples of unsupervised learning tasks include clustering and dimensionality reduction.
   The goal of reinforcement learning is to teach agents how to make a series of choices in a given situation in order to maximize a reward. It is frequently employed in robotics and gaming applications.
5. Model evaluation:
   Depending on the nature of the problem, it is crucial to evaluate the performance of a machine learning model after it has been trained using measures like accuracy, precision, recall, F1 score, or mean squared error.
6. HyperparameterTuning:
   Machine learning models have hyperparameters that are set before training rather than being learned from the data. Finding the ideal set of hyperparameters to optimize a model's performance is known as hyperparameter tuning.
7. UnderfittingAndOverfitting:
   Overfitting happens when a model overlearns the training set while underperforming on brand-new, untried data. On the other side, underfitting occurs when a model is too straightforward to identify the underlying trends in the data.
8. Deployment:
   A machine learning model can be used in real-world applications, including recommendation systems, fraud detection, natural language processing, computer vision, and autonomous cars, once it has been trained and validated.
9. EthicalConsiderations:
   Regarding bias in data and algorithms, privacy, transparency, and fairness, machine learning also creates ethical and societal issues. It's imperative to address these problems if we want to create AI responsibly.

With several applications in different sectors of the economy, including marketing, banking, and healthcare, machine learning is a rapidly developing field. It can fundamentally alter how we handle and apply data in order to tackle challenging issues and come to wise judgments.

Regression

For modeling and analyzing the relationships between variables, Regression is a fundamental statistical and machine-learning tool. It is mostly used to forecast a continuous outcome variable (dependent variable) from one or more input factors (independent variables), which might be continuous or categorical.

Finding the best-fit line or curve that illustrates the relationship between the independent factors and the dependent variable is the main objective of regression analysis. The regression model is the name given to this line or curve. Once the model has been trained on historical data, it can be applied to forecast new data or estimate the values of the dependent variable.

Regression'sPrimaryFeaturesAreAsFollows:

Let us look at some of the features of Regression and the types involved in the topic regression

VariousRegressions:

First, let us look at different types of Regression

1. LinearRegression:

• Regression that assumes a linear relationship between the dependent variable and one or more independent variables is known as a linear regression. In order to minimize the sum of squared discrepancies between the predicted and actual values, a straight line is sought. There are two types of linear Regression, Ridge regression, and lasso regression, which provide regularisation to avoid overfitting.

2. MultipleLinearRegression:

• Multiple linear Regression is used to model the relationship when there are multiple independent variables. These variables combine linearly to form the equation.

3. PolynomialRegression:

• This method fits a polynomial curve to the data when the relationship between the variables is not strictly linear.

4. LogisticRegression:

• Despite what its name suggests, Logistic Regression is utilized for classification tasks where the dependent variable is binary (for example, yes/no, 0/1). It simulates the likelihood of a binary result.

ModelAssessment:

• Metrics like Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), or R-squared (coefficient of determination) are frequently used in regression analysis to judge the model's quality.
• The effectiveness of the model can be assessed using cross-validation methods using various subsets of the data.

Assumptions:

• The assumption behind linear Regression is that the relationships between the independent and dependent variables are linear.
• Additionally, it presumes that the mistakes (or residuals) are regularly distributed, homoscedastic, and independent of one another.

Applications:

• Numerous disciplines, including economics, finance, the social sciences, engineering, and machine learning, use regression analysis.
• Predicting stock prices, estimating home values, examining the effect of marketing efforts on sales, and simulating the relationship between independent factors and health outcomes are examples of common applications.

Regularisation:

• By including a penalty component in the regression equation, regularisation methods like Ridge and Lasso regression work to avoid overfitting.
• In contrast to Lasso regression, which adds a punishment term based on the absolute values of coefficients, Ridge regression adds a penalty term based on the sum of squared coefficients.

Regression analysis is a potent method for deriving insights from real-world information, analyzing and modeling relationships within data, and making predictions. It has numerous applications in a wide range of fields, including statistics and machine learning.

RegressionTypesInDetail

Let us look at each Regression type deeply so that we get a better understanding of each Regression model.

1. SimpleLinearRegression

Simple Linear Regression is a statistical technique that involves fitting a linear equation to the observed data in order to represent the relationship between a single dependent variable (goal) and a single independent variable (predictor or feature). The independent and dependent variables are assumed to have a linear relationship. The model equation has the following form:

Y = B₀ + B₁X + ε

Where:

The aim (dependent variable) is Y.

The independent variable (feature or predictor) is X.

The intercept (the value of Y when X is 0) is equal to B0.

The slope, or the amount that Y varies for a unit change in X, is B1.

The error term (the discrepancy between the actual and expected values) is represented by the symbol.

Simple linear Regression, sometimes referred to as the least squares method, seeks to predict the values of B0 and B1 that minimize the sum of squared errors (SSE).

FormulasForSimpleLinearRegression:

Let us look at some of the most important formulas that are used while working on linear Regression.

1. Estimation of β₀ and β₁:
   β₁ (slope) = Σ((Xᵢ - Mean(X)) * (Yᵢ - Mean(Y))) / Σ((Xᵢ - Mean(X))²
   β₀ (intercept) = Mean(Y) - β₁ * Mean(X)
2. Prediction of Y for a given X:
   Ŷ = β₀ + β₁X
3. Residuals (Errors):
   Residual (εᵢ) = Yᵢ - Ŷᵢ
4. The sum of Squared Errors (SSE):
   SSE = Σ(εᵢ²)
5. Coefficient of Determination (R²):
   R² = 1 - (SSE / SST), where SST is the total sum of squares.

Example:

Let's go over a straightforward example of simple linear Regression to forecast a student's final exam grade (Y) based on the quantity of study time they put in (X).

Assume you have the dataset shown below:

1. Calculate the means of X and Y:

Mean(X) = (2 + 3 + 4 + 5 + 6) / 5 = 4

Mean(Y) = (65 + 75 + 82 + 88 + 92) / 5 = 80.4

2. Calculate the slope (β₁) using the formula:

β₁ = Σ((Xᵢ - Mean(X)) * (Yᵢ - Mean(Y))) / Σ((Xᵢ - Mean(X))²

β₁ = ((2-4)(65-80.4) + (3-4)(75-80.4) + (4-4)(82-80.4) + (5-4)(88-80.4) + (6-4)*(92-80.4)) / ((2-4)² + (3-4)² + (4-4)² + (5-4)² + (6-4)²)

β₁ ? 5.52

3. Calculate the intercept (β₀) using the formula:

β₀ = Mean(Y) - β₁ * Mean(X)

β₀ ? 80.4 - 5.52 * 4

β₀ ? 57.28

4. The linear regression equation is:

Y = 57.28 + 5.52X

Now, based on the quantity of study time, you can apply this equation to forecast your final exam results.

By including a regularisation element in the linear regression equation, the Ridge Regression and Lasso Regression procedures in linear Regression address the issue of multicollinearity and guard against overfitting. A description of both methods, along with their formulas and illustrations, is provided below:

RidgeRegression:

By including a regularisation element in the linear regression equation, the Ridge Regression and Lasso Regression procedures in linear Regression address the issue of multicollinearity and guard against overfitting. A description of both methods, along with their formulas and illustrations, is provided below:

Ridge Objective Function = SSE (Sum of Squared Errors) + λ * Σ(βᵢ²)

Where:

When performing simple linear or multiple linear Regression, SSE, or Sum of Squared Errors, is used.

The regularisation parameter, or λ (lambda), regulates the regularization's degree of strength.

The total of the squared coefficients is denoted by Σ(βᵢ²).

Ridge Regression attempts to reduce this objective function.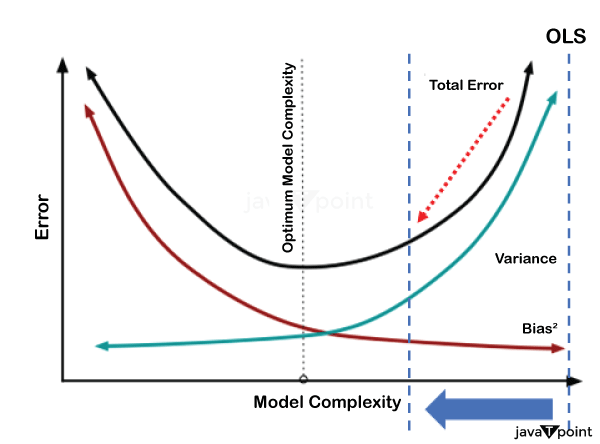

Example:

Assume you are using Ridge Regression to forecast home prices using two predictors: square footage (X1) and the number of bedrooms (X2).

Similar to multiple linear Regression, the Ridge Regression equation also includes a regularisation term:

Y = β₀ + β₁X₁ + β₂X₂ + λΣ(βᵢ²)

This equation can be used to minimize the objective function while estimating the coefficients β₀, β₁, and β₂.

LassoRegression:

Another method that includes a penalty element in the linear regression equation is called Lasso Regression, sometimes referred to as L1 regularisation. Lasso, in contrast to Ridge Regression, promotes model sparsity by bringing some coefficients to a precise zero value. The Lasso Regression's updated objective function is as follows:

Lasso Objective Function = SSE + λ * Σ|βᵢ|

Where:

When performing simple linear or multiple linear Regression, SSE, or Sum of Squared Errors, is used.

The regularisation parameter, denoted by λ (lambda), regulates the degree of regularisation.

The total of the absolute values of the coefficients is shown by the symbol Σ|βᵢ|.

Lasso regression attempts to reduce this objective function to the minimum while potentially reducing some coefficients to zero.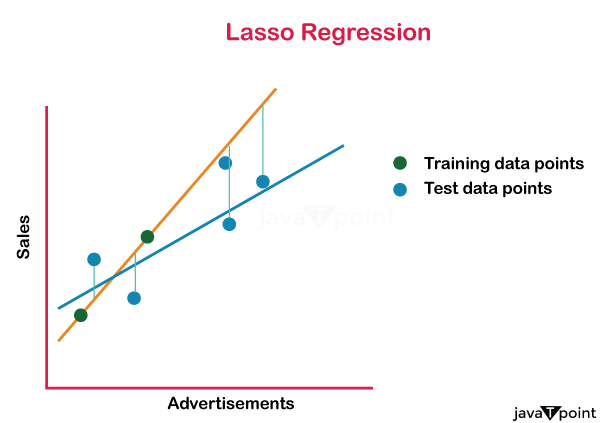

Example:

The Lasso Regression equation is as follows, using the same example of forecasting house prices with square footage (X1) and the number of bedrooms (X2) as predictors:

Y = β₀ + β₁X₁ + β₂X₂ + λΣ|βᵢ|

This equation can be used to minimize the objective function while estimating the coefficientsβ₀, β₁, and β₂. Some of the coefficients could be set exactly to zero via Lasso, choosing only the most crucial predictors for the model.

In real life, the regularisation parameter is set to a value that optimally balances model complexity and goodness of fit using methods like cross-validation. For managing multicollinearity and avoiding overfitting in linear regression models, Ridge and Lasso Regression are useful methods.

2. MultipleLinearRegression

An expansion of simple linear Regression, multiple linear Regression involves fitting a linear equation to the observed data to represent the relationship between a dependent variable (the target) and two or more independent variables (predictors or characteristics). The model's equation has the following form in multiple linear Regression:

Y = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ + ε

Where:

The aim (dependent variable) is Y.

The independent variables (predictors or characteristics) are X1, X2,..., and Xp.

The intercept is β₀.

The coefficients of the independent variables are β₀, β₁, β₂, …. βₚ

The error term (the discrepancy between the actual and expected values) is represented by the symbol.

Similar to simple linear Regression, the objective of multiple linear Regression is to estimate the values of β₀, β₁, β₂, …. βₚ that minimize the sum of squared errors (SSE).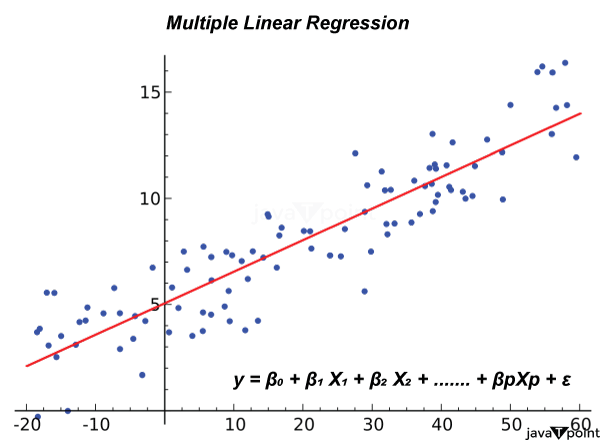

FormulasForMultipleLinearRegression:

1. Estimation of β₀, β₁, β₂, ..., βₚ:
   β₀ (intercept) = Mean(Y) - (β₁ * Mean(X₁) + β₂ * Mean(X₂) + ... + βₚ * Mean(Xₚ))
   βᵢ (coefficients for each feature) = Σ((Xᵢ - Mean(Xᵢ)) * (Y - Ŷ)) / Σ((Xᵢ - Mean(Xᵢ))²) for i = 1, 2, ..., p
2. Prediction of Y for a given set of X₁, X₂, ..., Xₚ:
   Ŷ = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ
3. Residuals (Errors):
   Residual (εᵢ) = Yᵢ - Ŷᵢ
4. The sum of Squared Errors (SSE):
   SSE = Σ(εᵢ²)
5. Coefficient of Determination (R²):
   R² = 1 - (SSE / SST), where SST is the total sum of squares.

Example:

Let's look at an illustration of multiple linear Regression to forecast the cost of a home (Y) based on two independent variables: the home's square footage (X1) and the number of bedrooms (X2).

Assume you have the dataset shown below:

Calculate the means of X₁, X₂, and Y:

Mean(X₁) = (1500 + 2000 + 1800 + 2200 + 1600) / 5 = 1820

Mean(X₂) = (3 + 4 + 3 + 5 + 4) / 5 = 3.8

Mean(Y) = (200,000 + 250,000 + 220,000 + 280,000 + 210,000) / 5 = 232,000

Estimate the coefficients (β₀, β₁, β₂) using the formulas:

β₀ (intercept) = Mean(Y) - (β₁ * Mean(X₁) + β₂ * Mean(X₂))

β₁ (coefficient for X₁) and β₂ (coefficient for X₂) are calculated similarly using the formula for each.

The multiple linear regression equation is:

Y = β₀ + β₁X₁ + β₂X₂

This equation can now be used to anticipate property prices depending on square footage and the number of bedrooms.

(4-4)(82-80.4) + (5-4)(88-80.4) + (6-4)*(92-80.4)) / ((2-4)² + (3-4)² + (4-4)² + (5-4)² + (6-4)²)

β₁ ? 5.52

5. Calculate the intercept (β₀) using the formula:

β₀ = Mean(Y) - β₁ * Mean(X)

β₀ ? 80.4 - 5.52 * 4

β₀ ? 57.28

6. The linear regression equation is:

Y = 57.28 + 5.52X

Now, based on the quantity of study time, you can apply this equation to forecast your final exam results.

By including a regularisation element in the linear regression equation, the Ridge Regression and Lasso Regression procedures in linear Regression address the issue of multicollinearity and guard against overfitting. A description of both methods, along with their formulas and illustrations, is provided below:

3. PolynomialRegression

Regression analysis that uses nth-degree polynomials to represent the relationship between the independent (predictor) and dependent (target) variables is known as polynomial Regression. This type of linear Regression uses polynomial equations to represent the relationship between the variables rather than linear equations. Regression using polynomials is very helpful when there is a curved pattern rather than a straight line between the variables.

The definition of polynomial Regression, along with its formula and an illustration, are given below:

FormulaForPolynomialRegression:

The equation for polynomial Regression is as follows:

Y = β₀ + β₁X + β₂X² + β₃X³ + ... + βₙXⁿ + ε

Where:

The aim (dependent variable) is Y.

X is a predictor that is an independent variable.

The coefficients of the polynomial terms are β₀, β₁, β₂, β₃, ..., βₙ.

The highest power of X employed in the equation is determined by the polynomial's degree, n.

The error term (the discrepancy between the actual and expected values) is represented by the symbol.

Similar to linear Regression, polynomial Regression aims to estimate the values of the coefficients β₀, β₁, β₂, β₃, ..., βₙ that minimize the sum of squared errors (SSE).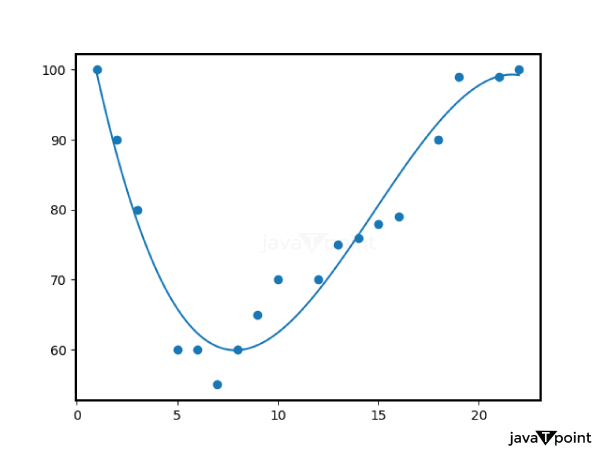

Example:

Let's look at an instance where you need to forecast the relationship between an individual's income (Y) and their number of years of work experience (X). The link is not linear because, with more years of experience, salaries tend to rise faster. A polynomial regression may be a good option in this situation.

Assume you have the dataset shown below:

If you use a polynomial with a degree of 2, for example, you will fit a quadratic equation when using polynomial Regression:

Assume you have the dataset shown below:

Y = β₀ + β₁X + β₂X² + ε

Now, while minimizing the SSE, use this equation to estimate the coefficients β₀, β₁, and β₂. This Regression can be carried out using a variety of statistical or machine-learning approaches, such as gradient descent or specialized regression libraries in Python or R.

Using the polynomial equation, you can make predictions after estimating the coefficients. For illustration, the following would be the compensation range for a person with six years of experience:

Incorporate X = 6 into the formula:

Y = β₀ + β₁(6) + β₂(6²)

To calculate Y, substitute the predicted coefficients.

In order to avoid overfitting or underfitting the data, it's crucial to select the right degree of the polynomial. Polynomial Regression is a versatile technique that may capture non-linear correlations between variables.

4. LogisticRegression

It is feasible to predict categorical outcomes with two possible values, commonly expressed as 0 and 1 (for example, yes/no, spam/not spam, pass/fail), using the statistical method known as logistic Regression. Contrary to what its name implies, Logistic Regression is a classification algorithm. Utilizing the logistic function to translate predictions to a probability between 0 and 1, it represents the likelihood that an input belongs to a specific class.

The definition of logistic Regression, along with its formula and an illustration, are given below:

FormulaForLogisticRegression:

The logistic (or sigmoid) function is used in the logistic regression model to simulate the likelihood that the dependent variable (Y) will be 1 (or fall into the positive class):

P(Y=1|X) = 1 / (1 + e^(-z))

Where:

The probability that Y is 1 given the input X is known as P(Y=1|X).

The natural logarithm's base, e, is about 2.71828.

The predictor variables are combined linearly to form z: z = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ

The coefficients for the predictor variables X1, X2,..., Xp are β₀, β₁, β₂, ..., βₚ .

For modeling probabilities, the logistic function makes sure that the result is confined between 0 and 1.

You normally select a decision threshold (like 0.5) to categorize the input into one of the two classes. If P(Y=1|X) is larger than the threshold, the input is categorized as 1; otherwise, it is categorized as 0.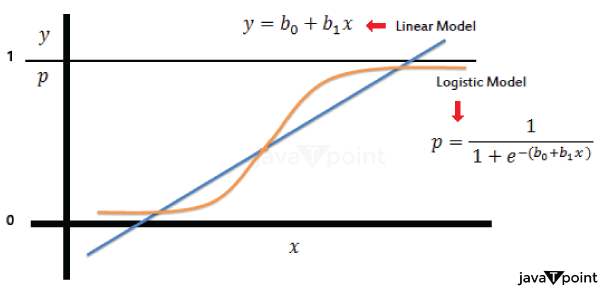

Example:

Let's look at an illustration where you want to forecast a student's exam result based on how many hours they studied (X) and whether they will pass (1) or fail (0).

Assume you have the dataset shown below:

In order to forecast whether a student who puts in a specific amount of study time will pass or fail, you should create a logistic regression model.

• The logistic regression formula's coefficients 0 and 1 are estimated by fitting the logistic regression model to your data using optimization techniques (such as gradient descent).
• Once the model has been trained, you can use it to forecast a student's likelihood of passing based on the amount of hours they spent studying.
• You use the estimated probability and a threshold (for example, 0.5) to categorize pupils as passing or failing. For instance, you would classify the student as a pass (1) if the projected probability was more than or equal to 0.5 and as a fail (0) otherwise.

For binary and multi-class classification issues, the classification algorithm known as logistic Regression is frequently employed in machine learning. When modeling the likelihood of an event occurring based on one or more predictor factors, it is especially helpful.

Conclusion

A fundamental method for modeling and predicting continuous outcomes based on the connections between variables in machine learning is Regression. It includes a range of methods, including straightforward linear Regression and more intricate ones like polynomial Regression, ridge, and lasso regression. These techniques give us the ability to measure and analyze the influence of predictor factors on the target variable, offering important insights into a variety of fields, including finance, healthcare, marketing, and more. Because of how easily they can be understood, regression models are highly valued as tools for both comprehending data relationships and making predictions.

In addition, thorough feature engineering and data pretreatment are frequently needed for regression approaches to produce reliable findings. Regression's crucial model selection and evaluation processes involve picking the best regression strategy and validating it with metrics like MSE and R2. Regression is a flexible and broadly applicable method in the machine learning toolkit that enables data scientists and analysts to create prediction models that improve decision-making processes in a variety of domains.