Variational AutoencodersThe development of sophisticated methods has occurred in the dynamic fields of artificial intelligence and machine learning due to the quest to produce fresh and creative data examples. Variational Autoencoders (VAEs), a paradigm that combines the worlds of neural networks and probabilistic modeling, has emerged as one of these. VAEs have created new opportunities in creative data production, picture synthesis, and data reduction thanks to their capacity to capture complicated data distributions and provide a variety of high-quality samples. Innovation has been sparked by the need for generative models that mimic real-world data distributions, and VAEs are at the forefront of this transformation. VAEs provide computers the ability to create wholly new instances that closely match the training data in addition to replicating already-existing data through the incorporation of probabilistic ideas into the framework of conventional autoencoders. VAEs may now not only reconstruct pictures but also create creative artwork, create realistic photographs, and even help with drug development thanks to this mix of creativity and statistical rigor. This article explores variational autoencoders, examining their inner workings, applicability across several domains, inherent difficulties, and ground-breaking research that keeps generative modeling from becoming what it once was. We will reveal how VAEs are transforming industries and opening up new horizons in artificial intelligence by focusing on the neural network and probabilistic reasoning combination that drives them. A Brief Overview of Variational Autoencoder ArchitectureVAEs, or variational autoencoders, revolutionize data production by fusing neural networks with probabilistic models. Their structure includes: Encoder: Creates a latent space representation of the input data and provides mean and variance parameters for a Gaussian distribution. Reparameterization Trick: Using encoder parameters to alter fixed Gaussian samples makes differentiable sampling possible and makes training easier. Latent Space: As a link between creativity and data, using samples as the basis for generating a variety of data. Decoder: To accurately reproduce the input data with minimal loss, the decoder converts latent space samples back into data space. Loss Function: Two terms in the loss function-reconstruction loss (data integrity) and regularization term (conforming to a structured latent distribution)-direct learning. 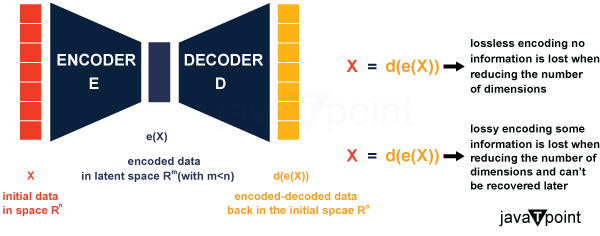
Variational Autoencoders' design is a masterful synthesis of probabilistic reasoning with neural networks. VAEs provide a symphony of invention through the encoder, reparameterization trick, latent space, decoder, and a thoroughly thought-out loss function that enables computers to comprehend data distributions and produce creative and cohesive new samples. Variational Autoencoders are primed to continue reshaping the landscape of generative modeling and creative AI as researchers continue to improve and build upon this architecture. The Mathematical Secrets of Variational AutoencodersIn addition to being a work of art in architecture, variational autoencoders (VAEs) are also a masterpiece in mathematics. They combine neural networks, optimization, and probability theory to forge a potent framework for generative modeling. Let's examine the mathematical underpinnings of VAEs to comprehend their fundamental nature. Probability Distributions and Latent Space: At the core of VAEs is modeling data with probability distributions. The latent space, often denoted as z, represents a lower-dimensional space where data points are mapped. This latent space follows a multivariate Gaussian distribution, z ~ N(μ, σ^2). The encoder learns to map input data to these distribution parameters, μ (mean) and log(σ^2) (log variance), thereby defining the latent space distribution. The Reparameterization Trick : This is where the trick is. Instead of choosing sites at random, we employ a translator; we use a translator - a friendly Gaussian with a mean of 0 and a standard deviation of 1. We call it "ε." This ε helps us shift and stretch so every point feels unique. We add μ and multiply by σ, and voilà! We've magically got a point from the latent space. This trick lets us learn the language of gradients, guiding us while we learn. Regularizing KL Divergence : Remember that we want our hidden world to have a little predictability, like a comfortable library. Therefore, to quantify how much our learning world deviates from a conventional one, we utilize a compass called KL divergence. Our loss function's regularization term ensures that we balance exploring and staying close to home. Reconstruction Loss : Let's now discuss the decoder. It transforms our secret code (latent vector) into artwork (reconstructed data) like a magician. Reconstruction loss is a metric to measure our work is realistic. If the artwork is hazy or off, we change the technique so that the artwork will look perfect the following time. Implementation: Variational Autoencoders (VAEs) are useful tools for innovative data creation and representation learning; they are not simply theoretical miracles. In this tutorial, we'll use Python and well-known machine-learning packages like TensorFlow and Keras to create a straightforward VAE. You'll have a practical grasp of creating and training your own VAE by the time it's all through. Setting up the EnvironmentMake sure Python and the required libraries are installed before we begin. For developing and training the VAE, you'll need TensorFlow or Keras (which uses TensorFlow's backend). Other deep learning libraries, such as PyTorch, are also available. Python code Construction of the VAE ArchitectureLet's design the VAE's architecture. We'll concentrate on a straightforward feedforward neural network in this case. Python code Creating the VAE ModelNow, let's put together the encoder and decoder to create the VAE model. Python code The Loss FunctionThe reconstruction loss (often mean squared error or binary cross-entropy) and the KL divergence loss make up the loss function for VAEs. We'll create unique loss functions using the Keras backend. Python code CompilationCompile the VAE model and train it with your dataset. Python code Generating SamplesOnce your VAE is trained, you can generate new samples by sampling from the latent space. python code And it completes the fundamental Variational Autoencoder implementation. This is obviously an oversimplified illustration, and you can extend it to include more intricate architectures, more datasets, and sophisticated methods like Normalizing Flows for higher sample quality. Only your creativity and available data will constrain the creative data production and representation learning potential of VAEs. What exactly is dimension reduction?Dimensionality reduction in machine learning is the process of lowering the number of characteristics used to represent a given set of data. This reduction can be helpful in a variety of circumstances that call for low dimensional data (data visualization, data storage, heavy computation...) and is accomplished either by selection (only some existing features are conserved) or by extraction (a reduced number of new features are created based on the old features). Even though there are several distinct approaches to dimensionality reduction, we can establish a general framework compatible with most (if not all!) of them. Let's first refer to the processes of encoding and decoding. Encoding produces the "new features" representation from the "old features" representation (either by selection or extraction). Therefore, dimension reduction may be seen as data compression, with the encoder compressing the data (from the original space to the encoded space, also known as latent space) and the decoder uncompressing it. Of course, this compression can be lossy, meaning that some information is lost while encoding and cannot be retrieved during decoding, depending on the original data distribution, the latent space dimension, and the encoder specification. ConclusionVariational Autoencoders' architecture represents a seamless fusion of neural networks and probabilistic reasoning. VAEs provide a symphony of invention through the encoder, reparameterization trick, latent space, decoder, and a thoroughly thought-out loss function that enables computers to comprehend data distributions and produce creative and cohesive new samples. Variational Autoencoders are primed to continue reshaping the landscape of generative modeling and creative AI as researchers continue to improve and build upon this architecture. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









