K-Means Clustering AlgorithmK-Means Clustering is an unsupervised learning algorithm that is used to solve the clustering problems in machine learning or data science. In this topic, we will learn what is K-means clustering algorithm, how the algorithm works, along with the Python implementation of k-means clustering. What is K-Means Algorithm?K-Means Clustering is an Unsupervised Learning algorithm, which groups the unlabeled dataset into different clusters. Here K defines the number of pre-defined clusters that need to be created in the process, as if K=2, there will be two clusters, and for K=3, there will be three clusters, and so on. It is an iterative algorithm that divides the unlabeled dataset into k different clusters in such a way that each dataset belongs only one group that has similar properties. It allows us to cluster the data into different groups and a convenient way to discover the categories of groups in the unlabeled dataset on its own without the need for any training. It is a centroid-based algorithm, where each cluster is associated with a centroid. The main aim of this algorithm is to minimize the sum of distances between the data point and their corresponding clusters. The algorithm takes the unlabeled dataset as input, divides the dataset into k-number of clusters, and repeats the process until it does not find the best clusters. The value of k should be predetermined in this algorithm. The k-means clustering algorithm mainly performs two tasks:
Hence each cluster has datapoints with some commonalities, and it is away from other clusters. The below diagram explains the working of the K-means Clustering Algorithm: 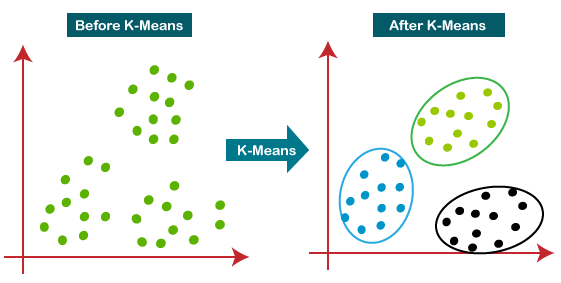
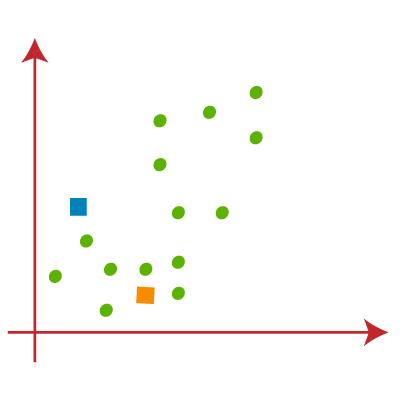
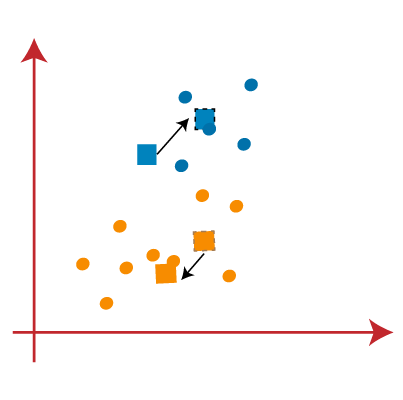
How does the K-Means Algorithm Work?The working of the K-Means algorithm is explained in the below steps: Step-1: Select the number K to decide the number of clusters. Step-2: Select random K points or centroids. (It can be other from the input dataset). Step-3: Assign each data point to their closest centroid, which will form the predefined K clusters. Step-4: Calculate the variance and place a new centroid of each cluster. Step-5: Repeat the third steps, which means reassign each datapoint to the new closest centroid of each cluster. Step-6: If any reassignment occurs, then go to step-4 else go to FINISH. Step-7: The model is ready. Let's understand the above steps by considering the visual plots: Suppose we have two variables M1 and M2. The x-y axis scatter plot of these two variables is given below: 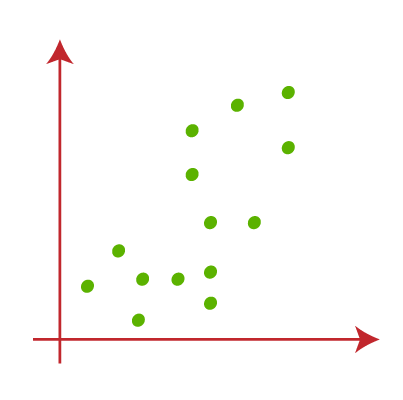
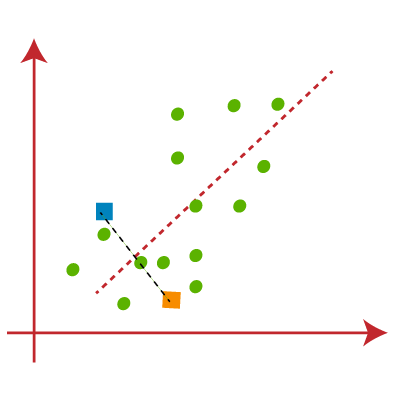
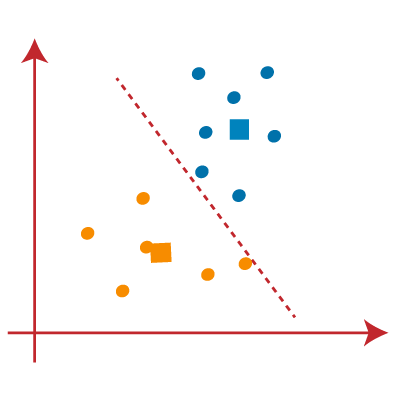
From the above image, it is clear that points left side of the line is near to the K1 or blue centroid, and points to the right of the line are close to the yellow centroid. Let's color them as blue and yellow for clear visualization. 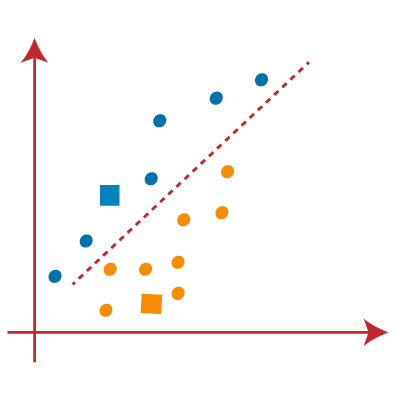
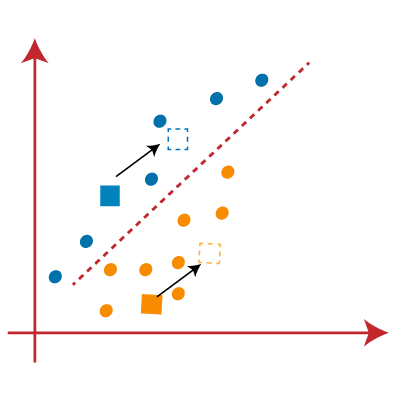
From the above image, we can see, one yellow point is on the left side of the line, and two blue points are right to the line. So, these three points will be assigned to new centroids. 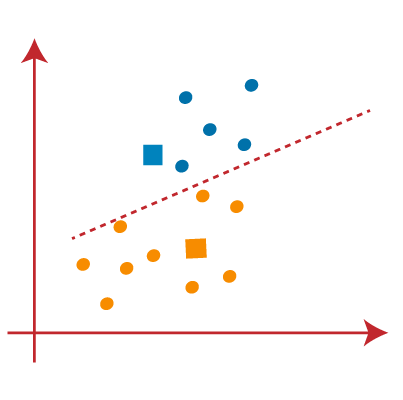
As reassignment has taken place, so we will again go to the step-4, which is finding new centroids or K-points.
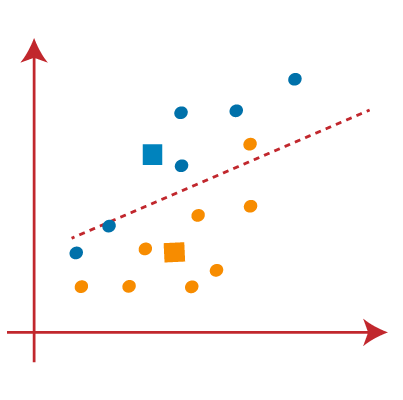
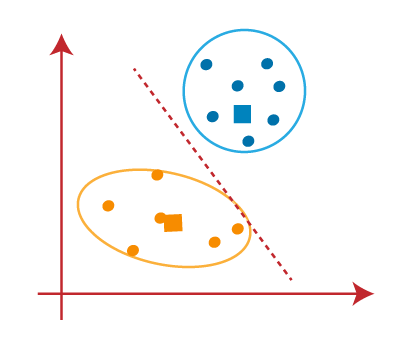
As our model is ready, so we can now remove the assumed centroids, and the two final clusters will be as shown in the below image: 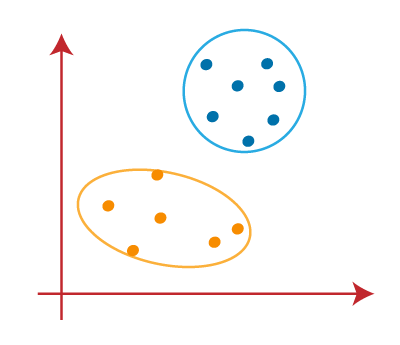
How to choose the value of "K number of clusters" in K-means Clustering?The performance of the K-means clustering algorithm depends upon highly efficient clusters that it forms. But choosing the optimal number of clusters is a big task. There are some different ways to find the optimal number of clusters, but here we are discussing the most appropriate method to find the number of clusters or value of K. The method is given below: Elbow MethodThe Elbow method is one of the most popular ways to find the optimal number of clusters. This method uses the concept of WCSS value. WCSS stands for Within Cluster Sum of Squares, which defines the total variations within a cluster. The formula to calculate the value of WCSS (for 3 clusters) is given below:
WCSS= ∑Pi in Cluster1 distance(Pi C1)2 +∑Pi in Cluster2distance(Pi C2)2+∑Pi in CLuster3 distance(Pi C3)2
In the above formula of WCSS, ∑Pi in Cluster1 distance(Pi C1)2: It is the sum of the square of the distances between each data point and its centroid within a cluster1 and the same for the other two terms. To measure the distance between data points and centroid, we can use any method such as Euclidean distance or Manhattan distance. To find the optimal value of clusters, the elbow method follows the below steps:
Since the graph shows the sharp bend, which looks like an elbow, hence it is known as the elbow method. The graph for the elbow method looks like the below image: 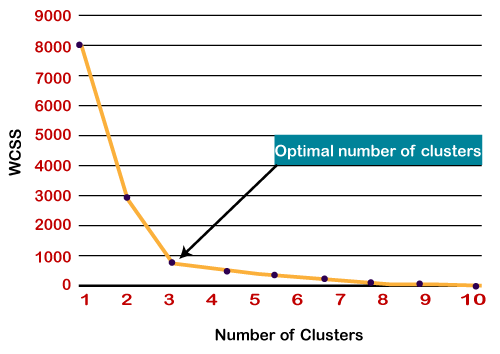
Note: We can choose the number of clusters equal to the given data points. If we choose the number of clusters equal to the data points, then the value of WCSS becomes zero, and that will be the endpoint of the plot.Python Implementation of K-means Clustering AlgorithmIn the above section, we have discussed the K-means algorithm, now let's see how it can be implemented using Python. Before implementation, let's understand what type of problem we will solve here. So, we have a dataset of Mall_Customers, which is the data of customers who visit the mall and spend there. In the given dataset, we have Customer_Id, Gender, Age, Annual Income ($), and Spending Score (which is the calculated value of how much a customer has spent in the mall, the more the value, the more he has spent). From this dataset, we need to calculate some patterns, as it is an unsupervised method, so we don't know what to calculate exactly. The steps to be followed for the implementation are given below:
Step-1: Data pre-processing StepThe first step will be the data pre-processing, as we did in our earlier topics of Regression and Classification. But for the clustering problem, it will be different from other models. Let's discuss it:
In the above code, the numpy we have imported for the performing mathematics calculation, matplotlib is for plotting the graph, and pandas are for managing the dataset.
By executing the above lines of code, we will get our dataset in the Spyder IDE. The dataset looks like the below image: 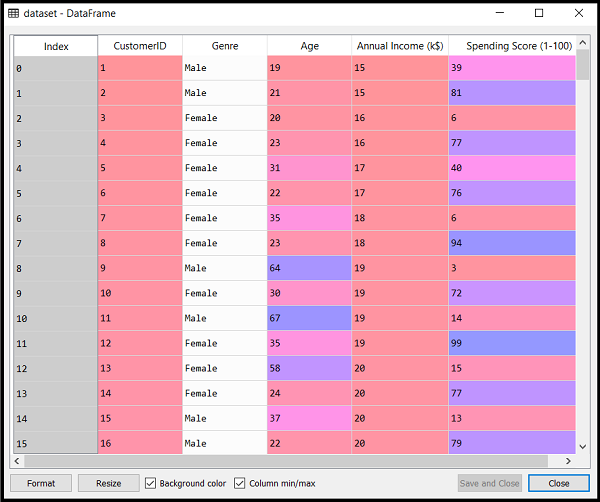
From the above dataset, we need to find some patterns in it.
Here we don't need any dependent variable for data pre-processing step as it is a clustering problem, and we have no idea about what to determine. So we will just add a line of code for the matrix of features. As we can see, we are extracting only 3rd and 4th feature. It is because we need a 2d plot to visualize the model, and some features are not required, such as customer_id. Step-2: Finding the optimal number of clusters using the elbow methodIn the second step, we will try to find the optimal number of clusters for our clustering problem. So, as discussed above, here we are going to use the elbow method for this purpose. As we know, the elbow method uses the WCSS concept to draw the plot by plotting WCSS values on the Y-axis and the number of clusters on the X-axis. So we are going to calculate the value for WCSS for different k values ranging from 1 to 10. Below is the code for it: As we can see in the above code, we have used the KMeans class of sklearn. cluster library to form the clusters. Next, we have created the wcss_list variable to initialize an empty list, which is used to contain the value of wcss computed for different values of k ranging from 1 to 10. After that, we have initialized the for loop for the iteration on a different value of k ranging from 1 to 10; since for loop in Python, exclude the outbound limit, so it is taken as 11 to include 10th value. The rest part of the code is similar as we did in earlier topics, as we have fitted the model on a matrix of features and then plotted the graph between the number of clusters and WCSS. Output: After executing the above code, we will get the below output: 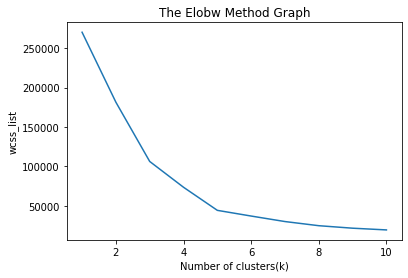
From the above plot, we can see the elbow point is at 5. So the number of clusters here will be 5. 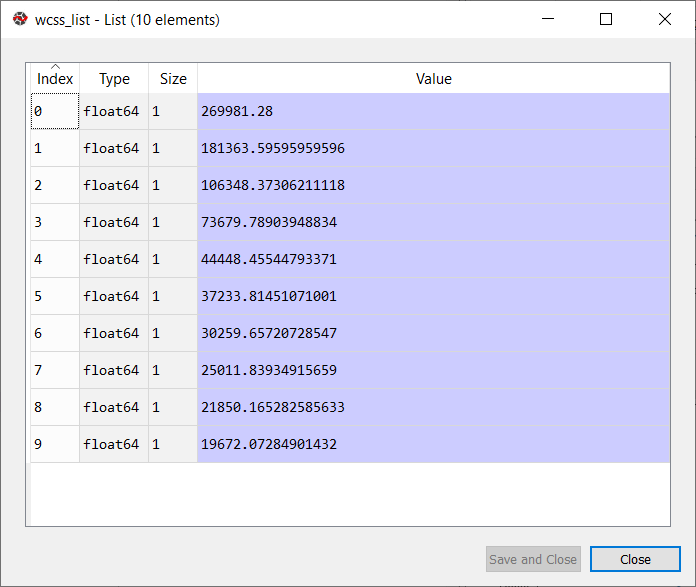
Step- 3: Training the K-means algorithm on the training datasetAs we have got the number of clusters, so we can now train the model on the dataset. To train the model, we will use the same two lines of code as we have used in the above section, but here instead of using i, we will use 5, as we know there are 5 clusters that need to be formed. The code is given below: The first line is the same as above for creating the object of KMeans class. In the second line of code, we have created the dependent variable y_predict to train the model. By executing the above lines of code, we will get the y_predict variable. We can check it under the variable explorer option in the Spyder IDE. We can now compare the values of y_predict with our original dataset. Consider the below image: 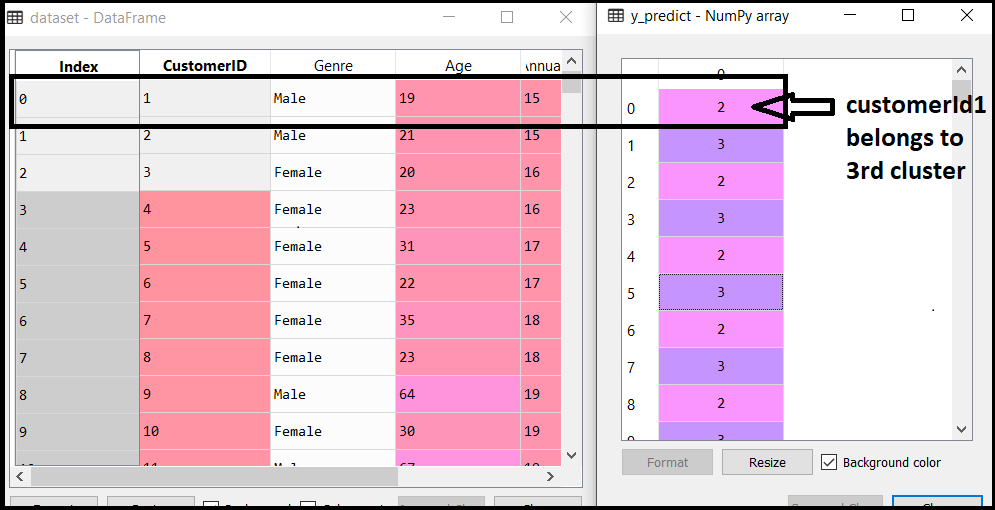
From the above image, we can now relate that the CustomerID 1 belongs to a cluster 3(as index starts from 0, hence 2 will be considered as 3), and 2 belongs to cluster 4, and so on. Step-4: Visualizing the ClustersThe last step is to visualize the clusters. As we have 5 clusters for our model, so we will visualize each cluster one by one. To visualize the clusters will use scatter plot using mtp.scatter() function of matplotlib. In above lines of code, we have written code for each clusters, ranging from 1 to 5. The first coordinate of the mtp.scatter, i.e., x[y_predict == 0, 0] containing the x value for the showing the matrix of features values, and the y_predict is ranging from 0 to 1. Output: 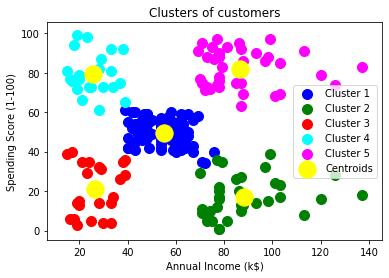
The output image is clearly showing the five different clusters with different colors. The clusters are formed between two parameters of the dataset; Annual income of customer and Spending. We can change the colors and labels as per the requirement or choice. We can also observe some points from the above patterns, which are given below:
Next TopicApriori Algorithm in Machine Learning
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share