Hidden Markov Model in Machine Learning
Hidden Markov Models (HMMs) are a type of probabilistic model that are commonly used in machine learning for tasks such as speech recognition, natural language processing, and bioinformatics. They are a popular choice for modelling sequences of data because they can effectively capture the underlying structure of the data, even when the data is noisy or incomplete. In this article, we will give a comprehensive overview of Hidden Markov Models, including their mathematical foundations, applications, and limitations.
What are Hidden Markov Models?
A Hidden Markov Model (HMM) is a probabilistic model that consists of a sequence of hidden states, each of which generates an observation. The hidden states are usually not directly observable, and the goal of HMM is to estimate the sequence of hidden states based on a sequence of observations. An HMM is defined by the following components:
- A set of N hidden states, S = {s1, s2, ..., sN}.
- A set of M observations, O = {o1, o2, ..., oM}.
- An initial state probability distribution, ? = {?1, ?2, ..., ?N}, which specifies the probability of starting in each hidden state.
- A transition probability matrix, A = [aij], defines the probability of moving from one hidden state to another.
- An emission probability matrix, B = [bjk], defines the probability of emitting an observation from a given hidden state.
The basic idea behind an HMM is that the hidden states generate the observations, and the observed data is used to estimate the hidden state sequence. This is often referred to as the forward-backwards algorithm.
Applications of Hidden Markov Models
Now, we will explore some of the key applications of HMMs, including speech recognition, natural language processing, bioinformatics, and finance.
- Speech Recognition
One of the most well-known applications of HMMs is speech recognition. In this field, HMMs are used to model the different sounds and phones that makeup speech. The hidden states, in this case, correspond to the different sounds or phones, and the observations are the acoustic signals that are generated by the speech. The goal is to estimate the hidden state sequence, which corresponds to the transcription of the speech, based on the observed acoustic signals. HMMs are particularly well-suited for speech recognition because they can effectively capture the underlying structure of the speech, even when the data is noisy or incomplete. In speech recognition systems, the HMMs are usually trained on large datasets of speech signals, and the estimated parameters of the HMMs are used to transcribe speech in real time.
- Natural Language Processing
Another important application of HMMs is natural language processing. In this field, HMMs are used for tasks such as part-of-speech tagging, named entity recognition, and text classification. In these applications, the hidden states are typically associated with the underlying grammar or structure of the text, while the observations are the words in the text. The goal is to estimate the hidden state sequence, which corresponds to the structure or meaning of the text, based on the observed words. HMMs are useful in natural language processing because they can effectively capture the underlying structure of the text, even when the data is noisy or ambiguous. In natural language processing systems, the HMMs are usually trained on large datasets of text, and the estimated parameters of the HMMs are used to perform various NLP tasks, such as text classification, part-of-speech tagging, and named entity recognition.
- Bioinformatics
HMMs are also widely used in bioinformatics, where they are used to model sequences of DNA, RNA, and proteins. The hidden states, in this case, correspond to the different types of residues, while the observations are the sequences of residues. The goal is to estimate the hidden state sequence, which corresponds to the underlying structure of the molecule, based on the observed sequences of residues. HMMs are useful in bioinformatics because they can effectively capture the underlying structure of the molecule, even when the data is noisy or incomplete. In bioinformatics systems, the HMMs are usually trained on large datasets of molecular sequences, and the estimated parameters of the HMMs are used to predict the structure or function of new molecular sequences.
- Finance
Finally, HMMs have also been used in finance, where they are used to model stock prices, interest rates, and currency exchange rates. In these applications, the hidden states correspond to different economic states, such as bull and bear markets, while the observations are the stock prices, interest rates, or exchange rates. The goal is to estimate the hidden state sequence, which corresponds to the underlying economic state, based on the observed prices, rates, or exchange rates. HMMs are useful in finance because they can effectively capture the underlying economic state, even when the data is noisy or incomplete. In finance systems, the HMMs are usually trained on large datasets of financial data, and the estimated parameters of the HMMs are used to make predictions about future market trends or to develop investment strategies.
Limitations of Hidden Markov Models
Now, we will explore some of the key limitations of HMMs and discuss how they can impact the accuracy and performance of HMM-based systems.
- Limited Modeling Capabilities
One of the key limitations of HMMs is that they are relatively limited in their modelling capabilities. HMMs are designed to model sequences of data, where the underlying structure of the data is represented by a set of hidden states. However, the structure of the data can be quite complex, and the simple structure of HMMs may not be enough to accurately capture all the details. For example, in speech recognition, the complex relationship between the speech sounds and the corresponding acoustic signals may not be fully captured by the simple structure of an HMM.
- Overfitting
Another limitation of HMMs is that they can be prone to overfitting, especially when the number of hidden states is large or the amount of training data is limited. Overfitting occurs when the model fits the training data too well and is unable to generalize to new data. This can lead to poor performance when the model is applied to real-world data and can result in high error rates. To avoid overfitting, it is important to carefully choose the number of hidden states and to use appropriate regularization techniques.
- Lack of Robustness
HMMs are also limited in their robustness to noise and variability in the data. For example, in speech recognition, the acoustic signals generated by speech can be subjected to a variety of distortions and noise, which can make it difficult for the HMM to accurately estimate the underlying structure of the data. In some cases, these distortions and noise can cause the HMM to make incorrect decisions, which can result in poor performance. To address these limitations, it is often necessary to use additional processing and filtering techniques, such as noise reduction and normalization, to pre-process the data before it is fed into the HMM.
- Computational Complexity
Finally, HMMs can also be limited by their computational complexity, especially when dealing with large amounts of data or when using complex models. The computational complexity of HMMs is due to the need to estimate the parameters of the model and to compute the likelihood of the data given in the model. This can be time-consuming and computationally expensive, especially for large models or for data that is sampled at a high frequency. To address this limitation, it is often necessary to use parallel computing techniques or to use approximations that reduce the computational complexity of the model.
Implementation of HMM using Python
For reference, we will implement the Hidden Markov Model for POS Tagging in the code.
Importing Libraries
Importing Data
Output:

Count the number of tags and words there are overall in the data. This will come in handy later.
Output:

We are unable to divide data properly using "train test split" since doing so would result in certain sentence components being included in the training set while others are included in the testing set. We substitute "GroupShuffleSplit" instead.
Output:
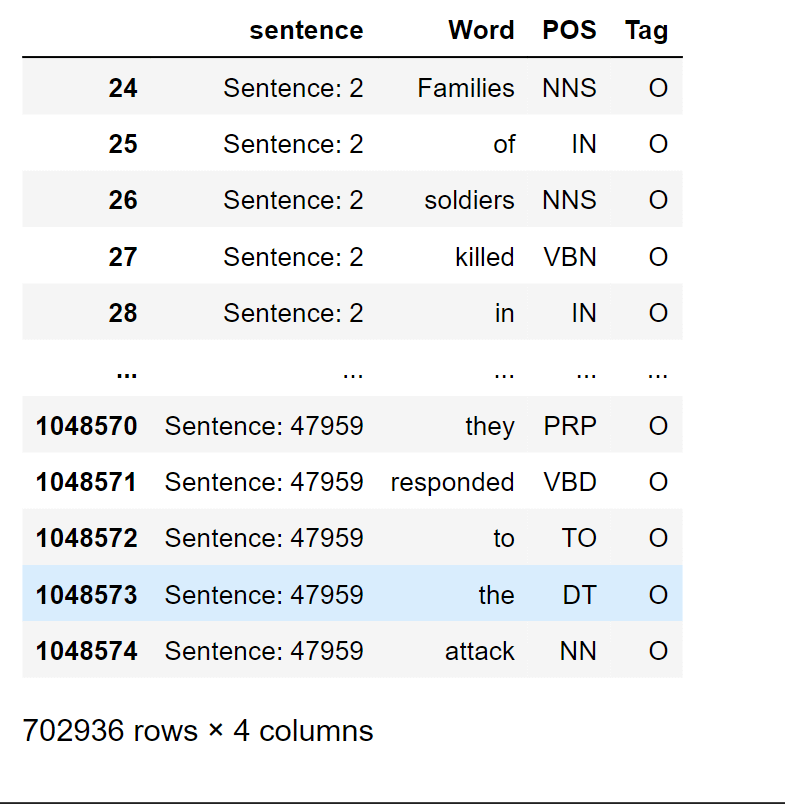
After examining the split data, everything seemed to be in order.
Verify the number of tags and words in the practice set.
Output:

The number of tags is sufficient, but the amount of words (29k vs 35k) is insufficient.
Due to this, we must erratically add some UNKNOWN words to the training dataset, after which we must recalculate the word list and generate a number-to-word mapping.
Output:

The Hidden Markov Model may be trained through the use of the Baum-Welch algorithm. However, the training's only input is a dataset (Words).
We are unable to link the states back to the POS tag.
Because of this, we must determine the model parameters for "hmmlearn."
Initialize HMM
We must first change certain words into the term "UNKNOWN" because they might not ever exist in the training set.
The "data test" is then divided into "samples" and "lengths" and sent to HMM.
Output:
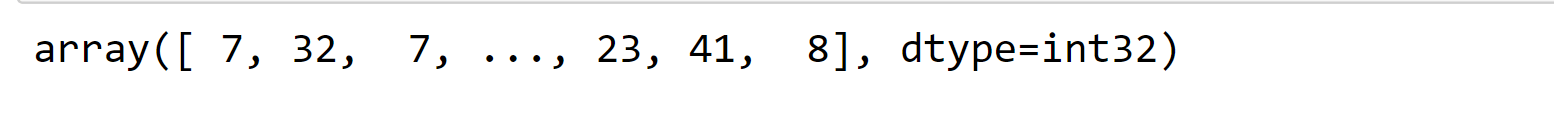
Output:
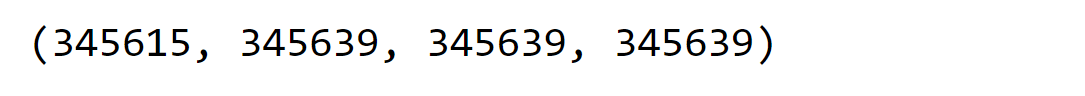
Output:
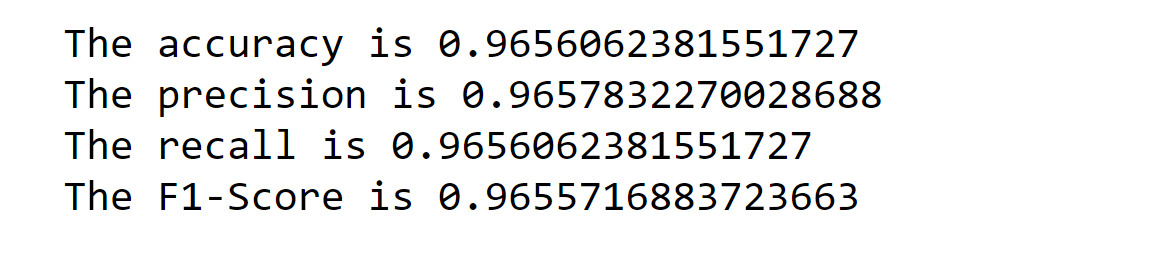
The accuracy for the HMM model is quite high which is around 96%.
|





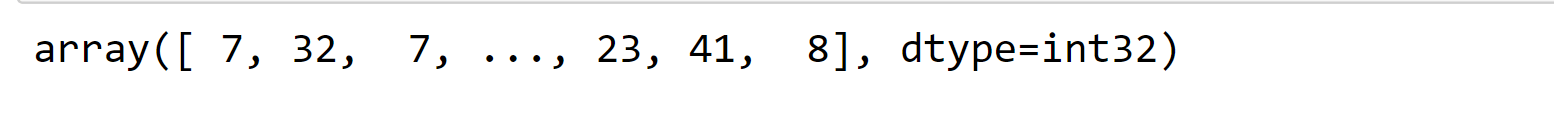
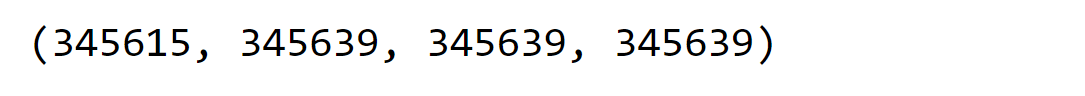
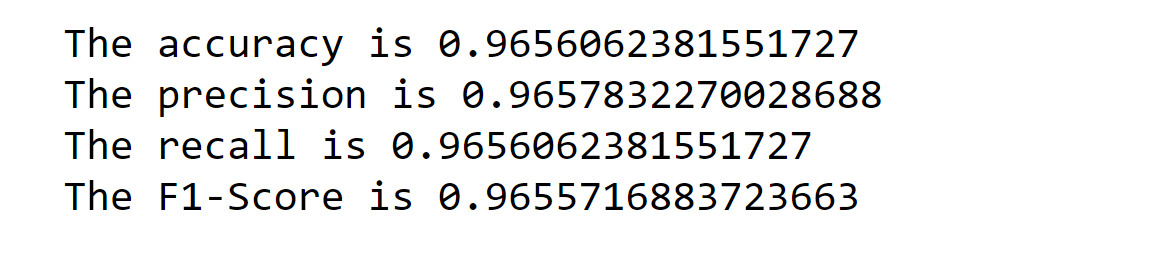
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









