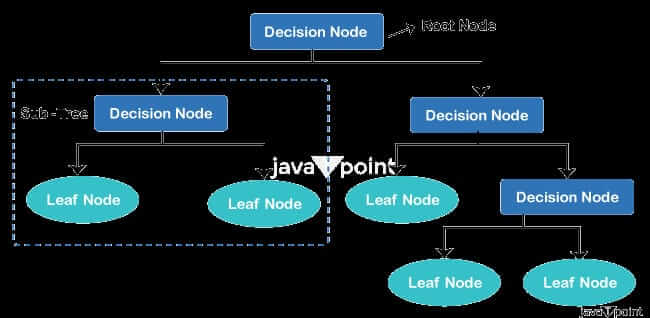
Decision Tree Classifier in Machine Learning

Decision Trees are a sort of supervised machine learning where the training data is continually segmented based on a particular parameter, describing the input and the associated output. Decision nodes and leaves are the two components that can be used to explain the tree. The choices or results are represented by the leaves. The data is divided at the decision nodes.

A well-liked machine learning approach for classification and regression tasks is the decision tree classifier. It is a supervised learning technique that creates a tree-like model of choices and potential outcomes.

The fundamental problem that emerges while developing a decision tree is how to choose the best attribute for the root node and for sub-nodes. So, a method known as attribute selection measure, or ASM, can be used to tackle these issues. By using this measurement, we can choose the ideal attribute for the tree nodes with ease. There are two widely used ASM approaches, which are as follows:

1. Gini index: The Gini index gauges a group of samples' impurity or inequality. It measures how effectively a specific property divides the data into homogeneous subsets in the context of decision trees. For a specific property, the Gini index is determined as follows:

(Sum of Squared Probabilities of Each Class in the Subset) - 1 = Gini_index

The Gini index has a range of 0 to 1, with 0 denoting a pure set (all samples are from the same class) and 1 denoting maximum impurity (equal distribution of samples among classes). The characteristic with the lowest Gini index is chosen as the optimal attribute for data splitting when creating a decision tree.

2. Information gain: A second criterion for assessing the quality of a split is information gain. It calculates the amount of entropy (uncertainty) that is reduced as a result of dividing the data by a specific property. A set of S's entropy is determined as follows:

Entropy(S) equals the sum of (p * log2(p)).

where p is the likelihood of each class in the set S. The difference between the entropy of the parent set S and the weighted average entropy of its child subsets following the split is used to calculate the information gain for a particular attribute.

Entropy(S) - weighted average of kid entropies equals information gain.

The optimal property for data splitting is chosen to have the most information gain.

Terminologies of Decision Tree

1. Decision Tree: A decision tree is a flowchart-like structure in which each leaf node represents a class label or a decision, and each inside node represents a test on an attribute.
2. Root Node: The topmost node from which all other nodes in a decision tree are derived. Based on the chosen attribute, it divides into child nodes to represent the complete dataset.
3. Internal Node: An attribute test represented by a node in a decision tree called an internal node. Based on the attribute value, it divides the dataset into subsets.
4. Leaf Node: In a decision tree, this node stands in for a decision or a class label. There are no child nodes of it.
5. An attribute is a characteristic or feature that is utilized to divide a dataset at a node. A decision tree's internal nodes each stand for an attribute test.
6. Splitting: The division of the dataset into more manageable subsets in accordance with the chosen attribute. It establishes the decision tree's structure.
7. Split Criterion: A parameter or measurement that assesses the effectiveness of a split. Gini impurity, entropy, and analytic distance are common split criteria.
8. Gini Impurity: A gauge of an example set's impurity or disorder. It shows the likelihood of classifying an example wrongly at a node.
9. Entropy: A metric for the disorder or impurity of a collection of samples. The dataset's ambiguity or unpredictability is quantified.
10. Information Gain: A measurement of the entropy or impurity reduction brought about by a split. The property that offers the greatest details on the class labels is chosen.
11. Pruning: Removing superfluous branches or nodes from a decision tree in order to lessen overfitting and increase generalization.
12. Overfitting: When a decision tree model too closely mimics the noise or random oscillations in the training data, it performs poorly on data that has not yet been observed.
13. Underfitting: This refers to a decision tree model that performs poorly on both training and test data because it is too simplistic and cannot identify the underlying patterns in the data.
14. Depth: The distance along the longest path in a decision tree from any leaf node to the root node. It establishes the tree's level of complexity.

Working/Algorithm of Decision Tree Classifier

An outline of a decision tree classifier's operation is provided below:

1. Data Preparation: You begin with a dataset of labeled samples, each of which has a set of input features and an associated output label or class. There should be numerical or categorical values for the features.
2. Tree Building: The algorithm begins by selecting the best feature from the dataset to split the data into two or more homogeneous subsets. This selection is typically based on metrics like information gain, Gini impurity, or entropy. The chosen feature becomes the root node of the tree.
3. Splitting: The selected feature is used to split the dataset into subsets based on its possible values. Each subset corresponds to a branch or child node of the root node. This process is repeated recursively for each subset, creating branches and child nodes until a stopping criterion is met.
4. Stopping Criteria: The stopping criteria can be based on a variety of different things, such as when the tree has reached its maximum depth when a node has a minimal number of samples, or when impurity or information gain has improved to a minimum.
5. Leaf Nodes: The tree's leaf nodes are formed once the halting requirement is attained. Depending on the problem (classification or regression) being addressed, each leaf node represents a class label or a regression value.
6. Prediction: The input features are passed through the decision tree by selecting the relevant branches based on the feature values in order to categorize a new, unseen example. The class label connected to the leaf node reached ultimately dictates the prediction.

Types of Decision Trees in Machine Learning

Classification Trees: These types of decision trees are employed in the solution of classification issues when the objective is to forecast the categorical class or label of an input instance. Each branch of the tree provides a potential value or range of values for each internal node, which each represents a feature or attribute. The expected class labels are shown by the leaf nodes.

Regression Trees: When attempting to predict a continuous numerical value, regression trees are employed to solve the problem. Each internal node represents a feature or attribute, and each branch represents a potential value or range of values for that feature. This is similar to classification trees. The expected numerical values are represented by the leaf nodes.

Multi-output Problem Decision Trees: These decision trees are used to solve problems with several output variables. A mixture of the projected values for the various outputs is represented by each leaf node in the tree.

Decision trees that have been pruned: Pruning is a strategy for preventing overfitting in decision trees. To increase generalization performance, pruned decision trees are developed by first generating a full tree and then eliminating or collapsing branches. This makes the tree more adept at handling hidden data and prevents it from becoming overly complex.

Random Forests: As an ensemble method, random forests integrate various decision trees to produce predictions. Using a unique portion of the training data and an arbitrary collection of characteristics, each tree in the random forest is independently constructed. The projections of each individual tree are combined to get the final prediction.

Gradient Boosted Trees: Another ensemble technique, gradient-boosting combines a number of weak learners (usually decision trees) to produce a powerful prediction model. The predictions of all the trees in the gradient boosted ensemble are added together to provide the final forecast. Each tree in the ensemble is constructed to rectify the errors generated by the previous trees.

These are just a few instances of decision tree structures that are often employed in the field of machine learning. Each kind offers different advantages and disadvantages, and the most appropriate type to put to use depends on the machine learning circumstance issues.

Advantages of Decision Tree Classifier

The advantages are mentioned below:

i) Interpretability: Decision trees give the decision-making process a clear and simple representation. People may readily comprehend and analyze the model because of its flowchart-like layout. It can aid in determining the key characteristics and how they affect the classification process.

ii) Decision trees are capable of handling a combination of numerical and categorical characteristics without the need for considerable preprocessing or feature engineering. Outliers and missing values are handled naturally by them.

iii) Relationships between features and the goal variable that are not linear can be captured by decision trees. They may simulate intricate decision-making processes and interactions between several features.

iv) Efficiency: Decision trees can be trained and used to produce predictions rather quickly. Decision trees are effective for handling huge datasets since their time complexity is often logarithmic in the number of training examples.

v) Handling of interactions and nonlinear effects: Decision trees are effective for jobs where feature interactions are critical to the classification process because they can capture interactions and nonlinear effects between features.

vi) Missing value handling: During the splitting process, decision trees can handle missing values by considering them as a separate category. This does away with the necessity for imputation methods.

Disadvantages of Decision Tree

Some of the disadvantages are;

i) Decision trees have the propensity to overfit the training set of data, particularly when the tree is too deep and intricate. When a tree overfits, it captures noise or unimportant patterns from the training data, making it difficult to generalize to new data.

ii) Lack of Robustness: Decision trees are easily perturbed by minor adjustments to the training set of data. A tree structure can alter considerably even with small adjustments. Decision trees are less stable than some other machine learning algorithms as a result of their lack of robustness.

iii) High Variance: Decision trees have the potential to have a high variance, which means that they may respond differently to slight changes in the training set of data. It may be challenging to evaluate the model's actual performance and reliability due to this volatility.

iv) Bias in Favor of Features with More Levels: When splitting features, decision trees frequently favor features with more levels or categories. Because of this tendency, traits with fewer levels could not have as much of an effect on the choice.

Conclusion

The classifier based on decision trees is a renowned and frequently used method because of its simplicity and comprehension. Although we will concentrate on its use as a classifier, it may be utilized for both classification and regression tasks.

We can infer the following about the decision tree classifier based on the information available up until September 2021:

1. Possibilities

- Interpretable: Since the decision-making process is transparently represented by decision trees, it is simpler to comprehend and explain the outcomes.

Decision trees can capture nonlinear relationships between features, which enables them to manage complex datasets.

- Feature Importance: To aid with feature selection and data comprehension, decision trees can rank features according to their significance.

- Robust to Outliers: Because they divide the feature space according to the values of the features, decision trees are comparatively robust to outliers.

2. Weaknesses: - Overfitting: If decision trees are not correctly regularised, they have a propensity to overfit the training set of data. This problem can be reduced by employing strategies like pruning, setting a limit depth, or ensemble methods (such as random forests).

- Instability: Because decision trees are sensitive to even little changes in the training data, various tree architectures may result. The forecasts of various trees can be averaged using ensemble methods to address this.

- Bias: Because more levels or values can lead to more partitions and possibly better splits, decision trees may be biased in favor of features with more levels or values.

3. Things to keep in mind: - Preprocessing: Decision trees can handle both numerical and categorical information directly and are not sensitive to scale. Even so, it is crucial to handle missing values, encode categorical categories, and, if necessary, deal with outliers while preprocessing the data.

Decision trees feature a number of hyperparameters that can influence how well they function, including the maximum depth, the minimum samples needed to split a node, and the criterion used to assess the quality of a split (such as Gini impurity or entropy). The model's performance can be enhanced by tuning these hyperparameters.

- Ensemble Methods: To increase their predictive value and address some of their shortcomings, decision trees can be paired with ensemble methods like random forests or gradient boosting.

In conclusion, the decision tree classifier is a strong and flexible machine learning algorithm. It excels at handling complex datasets, nonlinear relationships, and interpretability. It also has drawbacks including overfitting and instability, which can be eliminated by using the right regularisation strategies and ensemble approaches. To get the best results from a decision tree classifier, it is crucial to preprocess the data and tweak the hyperparameters.