Locally Weighted Linear Regression

Within the field of machine learning and regression analysis, Locally Weighted Linear Regression (LWLR) emerges as a notable approach that bolsters predictive accuracy through the integration of local adaptation. In contrast to conventional linear regression models, which presume a universal correlation among variables, LWLR acknowledges the significance of localized patterns and relationships present in the data. In the subsequent discourse, we embark on an exploration of the fundamental principles, diverse applications, and inherent advantages offered by Locally Weighted Linear Regression. Our aim is to shed light on its exceptional capacity to amplify predictive prowess and furnish intricate understandings of intricate datasets.

Fundamentally, LWLR manifests as a non-parametric regression algorithm that discerns the connection between a dependent variable and several independent variables. Notably, LWLR's distinctiveness emanates from its dynamic adaptability, which empowers it to bestow distinct weights upon individual data points contingent on their proximity to the target point under prediction. In essence, this algorithm accords greater significance to proximate data points, deeming them as more influential contributors in the prediction process.

Principles of Locally Weighted Linear Regression

LWLR functions on the premise that the association between the dependent and independent variables adheres to linearity; however, this relationship is allowed to exhibit variability across distinct sections within the dataset. This is achieved by employing an individual linear regression model for each prediction, employing a weighted least squares technique. The determination of weights is carried out through a kernel function, which bestows elevated weights upon data points in close proximity to the target point and diminishes the weights for those that are farther away.

Applications of Locally Weighted Linear Regression

Time Series Analysis: LWLR is particularly useful in time series analysis, where the relationship between variables may change over time. By adapting to the local patterns and trends, LWLR can capture the dynamics of time-varying data and make accurate predictions.
Anomaly Detection: LWLR can be employed for anomaly detection in various domains, such as fraud detection or network intrusion detection. By identifying deviations from the expected patterns in a localized manner, LWLR helps detect abnormal behavior that may go unnoticed using traditional regression models.
Robotics and Control Systems: In robotics and control systems, LWLR can be utilized to model and predict the behavior of complex systems. By adapting to local conditions and variations, LWLR enables precise control and decision-making in dynamic environments.

Benefits of Locally Weighted Linear Regression

Improved Predictive Accuracy: By considering local patterns and relationships, LWLR can capture subtle nuances in the data that might be overlooked by global regression models. This results in more accurate predictions and better model performance.
Flexibility and Adaptability: LWLR can adapt to different regions of the dataset, making it suitable for complex and non-linear relationships. It offers flexibility in capturing local variations, allowing for more nuanced analysis and insights.
Interpretable Results: Despite its adaptive nature, LWLR still provides interpretable results. The localized models offer insights into the relationships between variables within specific regions of the data, aiding in the understanding of complex phenomena.

Code:

For the sake of understanding, we will implement it into code.

# Locall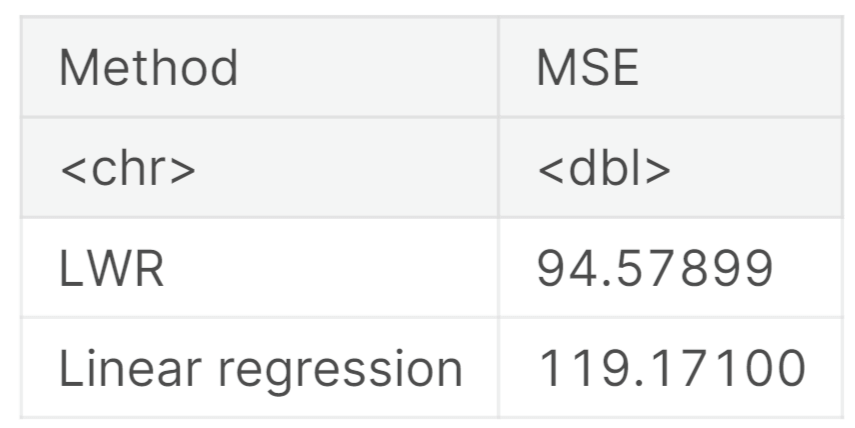y weighted linear regression (LWR)
k <- 5
k_folds <- createFolds(data$No, k)
tau <- 1000
MSE <- sapply(names(k_folds), function(fold) {
  train <- data[!No %in% k_folds[[fold]]]
  test <- data[No %in% k_folds[[fold]]]
  predictions <- sapply(seq.int(nrow(test)), function(observation) {
    X <- c(test[observation, X6_longitude], test[observation, X5_latitude])
    halversine <- sapply(seq.int(nrow(train)), function(obs) {
      X_i <- c(train[obs, X6_longitude], train[obs, X5_latitude])
      distm(X_i, X, fun = distHaversine)[1, 1]
    })
    weights <- exp(-(halversine^2 / (2 * tau^2)))
    model <- lm(Adjusted_house_price_per_unit_area
                ~ X2_house_age 
                + X3_distance_to_the_nearest_MRT_station
                + X4_number_of_convenience_stores,
                data = train,
                weights = weights)
    predict(model, test[observation])
  })
  MSE <- sum((test$Adjusted_house_price_per_unit_area - predictions)^2)
  MSE / nrow(test)
})
LWR <- mean(MSE)

# Linear regression
MSE <- sapply(names(k_folds), function(fold) {
  train <- data[!No %in% k_folds[[fold]]]
  test <- data[No %in% k_folds[[fold]]]
  model <- lm(Adjusted_house_price_per_unit_area
                ~ X2_house_age 
                + X3_distance_to_the_nearest_MRT_station
                + X4_number_of_convenience_stores,
                data = train)
  predictions <- sapply(seq.int(nrow(test)), function(observation) {
    predict(model, test[observation])
  })
  MSE <- sum((test$Adjusted_house_price_per_unit_area - predictions)^2)
  MSE / nrow(test)
})
LM <- mean(MSE)

# Display results
data.table(Method = c("LWR", "Linear regression"), MSE = c(LWR, LM))

Output:

In terms of Mean Squared Error (MSE), Locally Weighted Regression (LWR) outperforms traditional Linear Regression. With an MSE of 94.57899, LWR demonstrates superior predictive accuracy compared to Linear Regression, which has an MSE of 119.17100. This indicates that LWR provides more precise predictions and exhibits a better fit for the data. The improved performance of LWR can be attributed to its ability to incorporate local adaptation and consider the localized patterns and relationships within the dataset.

Conclusion

Locally Weighted Linear Regression (LWLR) emerges as a robust and effective method for augmenting predictive precision through the integration of local adaptation. By attentively scrutinizing the localized intricacies, patterns, and relationships inherent in the data, LWLR endows analysts with more intricate insights and precise predictions. Its inherent capability to adeptly adapt to diverse regions within the dataset renders it a highly sought-after tool in numerous domains, spanning time series analysis, anomaly detection, and robotics. As the realm of machine learning progresses ceaselessly, the indispensability of Locally Weighted Linear Regression persists, empowering both researchers and practitioners to extract profound knowledge from intricate datasets and thereby enrich their decision-making endeavors.

Next TopicMachine Learning in Restaurant Industry

← prev next →