Gini Index in Machine Learning

Introduction

Machine learning has reformed the manner in which we process and examine data, and decision tree algorithms are a famous decision for classification and regression tasks. The Gini Index, otherwise called the Gini Impurity or Gini Coefficient, is a significant impurity measure utilized in decision tree algorithms. In this article, we will investigate the idea of Gini Index exhaustively, its numerical formula, and its applications in machine learning. We will likewise contrast the Gini Index and other impurity measures, talk about its limitations and advantages, and inspect contextual analyses of its real-world applications. At long last, we will feature the future bearings for research around here.

What is Gini Index?

The Gini Index is a proportion of impurity or inequality in statistical and monetary settings. In machine learning, it is utilized as an impurity measure in decision tree algorithms for classification tasks. The Gini Index measures the probability of a haphazardly picked test being misclassified by a decision tree algorithm, and its value goes from 0 (perfectly pure) to 1 (perfectly impure).

Gini Index Formula

The Gini Index is a proportion of the impurity or inequality of a circulation, regularly utilized as an impurity measure in decision tree algorithms. With regards to decision trees, the Gini Index is utilized to determine the best feature to split the data on at every node of the tree.

The formula for Gini Index is as per the following: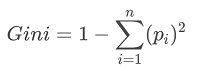

where pi is the probability of a thing having a place with a specific class.

For example, we should consider a binary classification issue with two classes An and B. On the off chance that the probability of class An is p and the probability of class B is (1-p), then the Gini Index can be calculated as:

The value of the Gini Index goes from 0.0 to 0.5 for binary classification problems, where 0.0 demonstrates a perfectly pure node (all examples have a place with a similar class) and 0.5 shows a perfectly impure node (tests are equally distributed across the two classes).

Using Gini Index in Classification Problems

The Gini Index is generally utilized as an impurity measure in decision tree algorithms for classification problems. In decision trees, every node addresses an element, and the objective is to split the data into subsets that are essentially as pure as could be expected. The impurity measure (like Gini Index) is utilized to decide the best split at every node.

To illustrate this, we should consider an example of a decision tree for a binary classification issue. The tree has two elements: age and income, and the objective is to foresee regardless of whether an individual is probably going to purchase an item. The tree is constructed utilizing the Gini Index as the impurity measure.

At the root node, the Gini Index is calculated in view of the probability of the examples having a place with class 0 or class 1. The node is split in view of the component that outcomes in the most elevated decrease in Gini Index. This cycle is rehashed recursively for every subset until a stopping measure is met.

Decision Trees

A decision tree is a well-known machine learning algorithm that is utilized for both classification and regression tasks. A model is worked by recursively splitting the dataset into more modest subsets in light of the values of the info highlights, determined to limit the impurity of the subsequent subsets.

At every node of the tree, a decision is made in view of the values of one of the info highlights, with the end goal that the subsequent subsets are basically as pure as could really be expected. The purity of a subset is regularly estimated by an impurity measure, for example, the Gini Index or the entropy.

The decision tree algorithm can be utilized for both binary and multi-class classification tasks, as well as regression tasks. In binary classification tasks, the decision tree splits the dataset into two subsets in light of the value of a binary feature, like yes or no. In multi-class classification tasks, the decision tree splits the dataset into numerous subsets in light of the values of a straight out feature, like red, green, or blue.

Gini Index vs Other Impurity Measures

Apart from the Gini Index, there are other impurity measures that are normally utilized in decision tree algorithms, for example, entropy and information gain.

Entropy:

In machine learning, entropy is a proportion of the irregularity or vulnerability in a bunch of data. It is generally utilized as an impurity measure in decision tree algorithms, alongside the Gini Index.

In decision tree algorithms, entropy is utilized to decide the best component to split the data on at every node of the tree. The objective is to find the element that outcomes in the biggest decrease in entropy, which relates to the component that gives the most information about the classification issue.

While entropy and the Gini Index are both normally utilized as impurity measures in decision tree algorithms, they have various properties. Entropy is more delicate to the circulation of class names and will in general deliver more adjusted trees, while the Gini Index is less touchy to the appropriation of class marks and will in general create more limited trees with less splits. The decision of impurity measure relies upon the particular issue and the attributes of the data.

Information gain:

Information gain is an action used to assess the nature of a split while building a decision tree. The objective of a decision tree is to split the data into subsets that are basically as homogeneous as conceivable as for the objective variable, so the subsequent tree can be utilized to make exact expectations on new data. Information gain measures the decrease in entropy or impurity accomplished by a split. The feature with the most noteworthy information gain is chosen as the best feature to split on at every node of the decision tree.

Information gain is a normally involved measure for assessing the nature of splits in decision trees, yet it isn't the one to focus on. Different measures, for example, the Gini index or misclassification rate, can likewise be utilized. The decision of splitting basis relies upon the main issue and the attributes of the dataset being utilized.

Example of Gini index

We should consider a binary classification issue where we have a dataset of 10 examples with two classes: "Positive" and "Negative". Out of the 10 examples, 6 have a place with the "Positive" class and 4 have a place with the "Negative" class.

To calculate the Gini Index of the dataset, we initially calculate the probability of each class:

p_1 = 6/10 = 0.6 (Positive)

p_2 = 4/10 = 0.4 (Negative)

Then, at that point, we utilize the Gini Index formula to calculate the impurity of the dataset:

Gini(S) = 1 - (p_1^2 + p_2^2)

= 1 - (0.6^2 + 0.4^2)

= 0.48

So, the Gini Index of the dataset is 0.48.

Presently suppose we need to split the dataset on an element "X" that has two potential values: "A" and "B". We split the dataset into two subsets in view of the component:

Subset 1 (X = A): 4 Positive, 1 Negative

Subset 2 (X = B): 2 Positive, 3 Negative

To calculate the decrease in Gini Index for this split, we initially calculate the Gini Index of every subset:

Gini(S_1) = 1 - (4/5)^2 - (1/5)^2 = 0.32

Gini(S_2) = 1 - (2/5)^2 - (3/5)^2 = 0.48

Then, we utilize the information gain formula to calculate the decrease in Gini Index:

IG(S, X) = Gini(S) - ((5/10 * Gini(S_1)) + (5/10 * Gini(S_2)))

= 0.48 - ((0.5 * 0.32) + (0.5 * 0.48))

= 0.08

So, the information gain (i.e., decrease in Gini Index) for splitting the dataset on highlight "X" is 0.08.

For this situation, in the event that we calculate the information gain for all elements and pick the one with the most noteworthy information gain, that component would be chosen as the best component to split on at the root node of the decision tree.

Advantages:

The Gini index is a broadly involved measure for evaluating the nature of splits in decision trees, and it enjoys a few upper hands over different measures, for example, entropy or misclassification rate. Here are a portion of the main advantages of using the Gini index:

Computationally efficient: The Gini index is a less complex and computationally quicker measure contrasted with different measures, for example, entropy, which involves calculating logarithms.

Intuitive interpretation: The Gini index is straightforward and interpret. It measures the probability of a haphazardly chosen example from a set being incorrectly classified in the event that it were haphazardly marked according to the class conveyance in the set.

Good for binary classification: The Gini index is especially powerful for binary classification problems, where the objective variable has just two classes. In such cases, the Gini index is known to be more steady than different measures.

Robust to class imbalance: The Gini index is less delicate to class imbalance contrasted with different measures, for example, precision or misclassification rate. This is on the grounds that the Gini index depends on the general extents of examples in each class as opposed to the outright numbers.

Less prone to overfitting: The Gini index will in general make more modest decision trees contrasted with different measures, which makes it less prone to overfitting. This is on the grounds that the Gini index will in general favor features that make more modest parcels of the data, which diminishes the possibilities overfitting.

Disadvantages:

While the Gini index enjoys a few benefits as a splitting measure for decision trees, it likewise has a few disadvantages. Here are a portion of the main downsides of using the Gini index:

Bias towards features with many categories: The Gini index will in general lean toward features with many categories or values, as they can make more splits and parcels of the data. This can prompt overfitting and a more complicated decision tree.

Not good for continuous variables: The Gini index isn't appropriate for continuous variables, as it requires discretizing the variable into categories or bins, which can prompt loss of information and diminished exactness.

Ignores feature interactions: The Gini index just thinks about the individual prescient force of each feature and ignores interactions between features. This can prompt poor splits and less exact forecasts.

Not ideal for some datasets: at times, the Gini index may not be the ideal measure for evaluating the nature of splits in a decision tree. For example, in the event that the objective variable is exceptionally slanted or imbalanced, different measures, for example, information gain or gain proportion might be more suitable.

Prone to bias in presence of missing values: The Gini index can be biased in the presence of missing values, as it will in general lean toward features with less missing values, regardless of whether they are not the most informative.

Real-World Applications of Gini Index

The Gini Index has been utilized in different applications in machine learning, for example, extortion location, credit scoring, and client division. For example, in extortion discovery, the Gini Index can be utilized to distinguish designs in exchange data and recognize bizarre way of behaving. In credit scoring, the Gini Index can be utilized to foresee the probability of default in view of variables like income, relationship of outstanding debt to take home pay, and record of loan repayment. In client division, the Gini Index can be utilized to bunch clients in view of their way of behaving and inclinations.

Future Research

Notwithstanding its boundless use in decision tree algorithms, there is still degree for research on the Gini Index. One area of research is the advancement of new impurity measures that can address the limitations of the Gini Index, like its inclination towards factors with many levels. One more area of research is the streamlining of decision tree algorithms utilizing the Gini Index, for example, the utilization of outfit techniques to work on the precision of decision trees.

Conclusion

The Gini Index is a significant impurity measure utilized in decision tree algorithms for classification tasks. It measures the probability of a haphazardly picked test being misclassified by a decision tree algorithm, and its value goes from 0 (perfectly pure) to 1 (perfectly impure). The Gini Index is straightforward and carry out, computationally productive, and powerful to exceptions. It has been utilized in different applications in machine learning, for example, misrepresentation discovery, credit scoring, and client division. While the Gini Index has a few limitations, there is still degree for research on its improvement and improvement of new impurity measures.