Introduction to SIFT( Scale Invariant Feature Transform)

Introduction

In the quickly developing field of computer vision, where images and videos act as a digital passage to seeing the world, algorithms that empower machines to distinguish and comprehend visual features hold a huge spot. Among these algorithms, the Scale-Invariant Feature Transform (SIFT) stands apart as a spearheading procedure that has transformed how we break down and control visual information. Whether it's perceiving objects, sewing scenes, or following features across images, SIFT's exceptional capacity to catch and portray particular features has made it a foundation in computer vision applications.

In this extensive guide, we set out on a journey to uncover the complexities of SIFT. From its primary ideas to its intricate recipes, we will plunge profound into the inward operations of this algorithm, revealing insight into how it accomplishes scale and revolution invariance, produces one-of-a-kind descriptors, and matches key features across images. With a solid spotlight on lucidity and openness, we will disentangle SIFT's center ideas and conditions, guaranteeing that peruses, whether novices to computer vision or old pros, can get a handle on its importance and potential.

Thus, whether you're an understudy anxious to get a handle on the basics of feature detection or a designer looking to outfit SIFT's power for your tasks, go along with us as we leave on a journey to open the capability of the Scale-Invariant Feature Transform. How about we plunge into the universe of SIFT, where particular features and invariance to transformations reclassify the limits of computer vision abilities?

SIFT( Scale Invariant Feature Transform)

1. Scale Space Representation

Scale-space representation is a principal idea in the SIFT algorithm that permits it to catch features at various scales inside an image. In reality, items can seem bigger or more modest because of varieties in distance or camera settings. Scale-space is built by convolving the first image with Gaussian kernels of expanding size (scale) to make a pyramid of images, where each level of the pyramid addresses the image at an alternate scale. The reason for this pyramid is to recognize features at various scales, empowering SIFT to be hearty to changes in object size. By distinguishing features across this pyramid, SIFT guarantees that the algorithm can perceive items or examples no matter what their scale, adding to its wonderful adaptability.

2. Key Points

Key points, frequently alluded to as key features, are unmistakable points inside an image that SIFT distinguishes and uses to address the substance of the image. These key points are significant because they stay stable across various scales, rotations, and lighting conditions. SIFT recognizes potential key points by looking at the differences in power between neighboring scales in the scale space pyramid, a cycle known as the Difference-of-Gaussian (Canine) pyramid. By finding the nearby extrema in the Canine pyramid, SIFT pinpoints key points that are striking and extraordinary, filling in as anchors for additional handling and examination.

Example:

Image 1

Image 2: Key points Detected from the Image 1

Image 3: Key points Detected from the Image 2

3. Orientation Assignment

Once key points are identified, SIFT relegates orientations to them. The objective is to guarantee that these key points are invariant to scale and revolution as well as have a reliable reference outline. To accomplish this, SIFT ascertains the gradient magnitude and orientation at every pixel in the key point's area. A histogram of gradient orientations is developed, and the peak(s) in this histogram shows the prevailing orientation(s) of the key point. This orientation data adjusts the key point's reference outline, permitting SIFT to deal with objects that are turned or situated contrastingly in different images.

4. Feature Descriptor

A feature descriptor is a minimized representation of the key point's neighborhood appearance, which catches the fundamental qualities of the feature. SIFT creates a descriptor for each key point by thinking about the gradient magnitudes and orientations inside its area. This area is separated into subregions, and histograms of gradient orientations are registered for every subregion. The histograms are connected to frame the last descriptor, bringing about a high-layered vector that embodies the key point's one-of-a-kind appearance. These descriptors empower SIFT to precisely look at and match features across various images.

5. Matching and Verification

Once key points and their descriptors are extricated from various images, SIFT intends to track down correspondences between them. Key points are matched by looking at their descriptors utilizing measurements like Euclidean distance or cosine similitude. Nonetheless, not all matches are exact because of commotion or incorrect key points. To address this, SIFT frequently utilizes a verification interaction utilizing methods like RANSAC (Irregular Example Agreement). RANSAC helps eliminate erroneous matches and assesses transformation boundaries (like interpretation and pivot) that precisely adjust the matched key points.

Formulas:

1. Gaussian Blurring

With regards to SIFT, Gaussian blurring is applied to make a scale space pyramid. The Gaussian capability at a particular scale σ is convolved with the first image to create an image that is smoothed at that scale. The blurring assists with eliminating fine subtleties, featuring bigger scale structures in the image. This smoothed image is then used to figure the Difference-of-Gaussian (DoG) images.

2. Difference-of-Gaussian (DoG)

The DoG image is a basic part of SIFT, filling in as an essential move toward distinguishing potential key points. This interaction upgrades features that are unmistakable at specific scales while smothering others. The DoG pyramid is then used to distinguish nearby extrema, which are potential key points.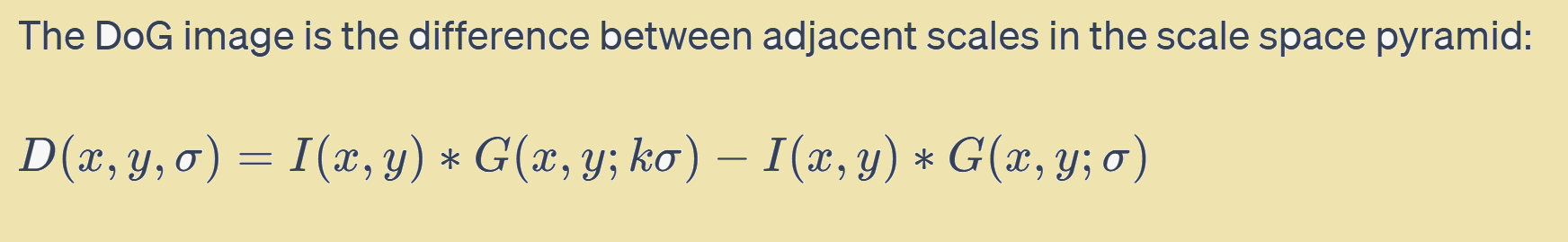

3. Gradient Magnitude and Orientation

Gradient magnitude and orientation are fundamental for allocating orientations to key points. In SIFT, gradients are determined by taking halfway subordinates of the image power in the θ(x,y) shows the course of the gradient. These qualities assist with deciding the predominant gradient bearing inside a key point's district and are utilized to make histograms for orientation assignments.

4. Histogram of Gradients (HoG) for Descriptor

The histogram of gradients is a basic move toward creating an unmistakable descriptor for each key point. In SIFT, the orientation data gathered from the past step is quantized into orientation canisters. The gradient magnitudes in each receptacle are collected to frame a histogram. This histogram catches the dissemination of gradient orientations inside a key point's area. The prevailing orientations, those with the most elevated values in the histogram, become the key point's orientations. This descriptor is then used to address the key point's nearby appearance.

5. Matching and Verification

The descriptors created for key points are utilized for matching and verification between images. Euclidean distance or cosine similitude measures are regularly used to look at the descriptors of key points in various images. This examination recognizes potential matches between key points. In any case, not all matches are precise because of commotion or exceptions. Verification methods like RANSAC (Arbitrary Example Agreement) are utilized to approve matches and gauge transformations that precisely adjust the matched key points.

Applications

1. Key Point Detection

Envision distinguishing key points on an image of a transcribed digit. SIFT would recognize corners and convergences of lines as key points, assisting with addressing the digit's remarkable features.

2. Object Recognition

For object recognition, SIFT recognizes key points on an item and matches them across different images. This empowers the algorithm to perceive the article in any event when it shows up at various scales or orientations.

3. Panorama Stitching

In panorama stitching, SIFT distinguishes key points in various images of a scene and matches them to accurately adjust the images. This guarantees that covering regions are flawlessly blended, making an all-encompassing perspective.

Original Images:

After Panorama Stitching:

Conclusion

In the domain of computer vision, the Scale-Invariant Feature Transform (SIFT) remains a guide for development and refinement. As we wrap up our investigation of this noteworthy algorithm, we find ourselves outfitted with a more profound comprehension of its inward functions, its numerical establishments, and its genuine applications.

SIFT's capacity to catch and portray unmistakable features, while staying invariant to scale, pivot, and light changes, has re-imagined how we see and connect with visual information. From object recognition to panorama stitching, SIFT's effect resounds across a huge number of uses, consistently coordinating into our lives and ventures. The quest for computer vision's outskirts proceeds, with SIFT filling in as an immortal demonstration of what can be accomplished when imagination, math, and innovation meet. In our current reality where visual information rules, SIFT's heritage perseveres, motivating future developments and pushing us toward a future where machines see as well as genuinely grasp the visual world around them. Thus, as we bid goodbye to this investigation, let us convey forward the transformative force of SIFT, supporting the boundless potential outcomes it brings to the very front of computer vision and then some.