Probabilistic Model in Machine Learning

A Probabilistic model in machine learning is a mathematical representation of a real-world process that incorporates uncertain or random variables. The goal of probabilistic modeling is to estimate the probabilities of the possible outcomes of a system based on data or prior knowledge.

Probabilistic models are used in a variety of machine learning tasks such as classification, regression, clustering, and dimensionality reduction. Some popular probabilistic models include:

• Gaussian Mixture Models (GMMs)
• Hidden Markov Models (HMMs)
• Bayesian Networks
• Markov Random Fields (MRFs)

Probabilistic models allow for the expression of uncertainty, making them particularly well-suited for real-world applications where data is often noisy or incomplete. Additionally, these models can often be updated as new data becomes available, which is useful in many dynamic and evolving systems.

For better understanding, we will implement the probabilistic model on the OSIC Pulmonary Fibrosis problem on the kaggle.

Problem Statement: "In this competition, you'll predict a patient's severity of decline in lung function based on a CT scan of their lungs. You'll determine lung function based on output from a spirometer, which measures the volume of air inhaled and exhaled. The challenge is to use machine learning techniques to make a prediction with the image, metadata, and baseline FVC as input."

Importing Libraries

EDA

Let's see this decline in lung function for three different patients.

Output: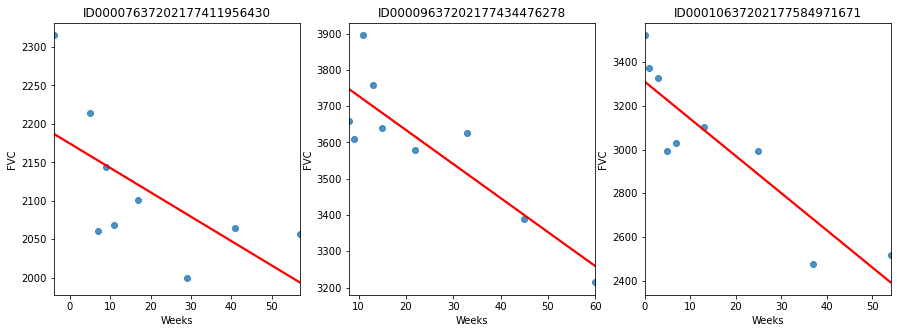

It is clearly obvious that lung capacity is declining. Yet as we can see, they vary greatly from case to patient.

Postulate the model

It's time to become imaginative. This tabular dataset might be modeled in a variety of ways. Here are a few tools we might employ:

• Hidden Markov Models
• Gaussian Processes
• Variational Auto Encoders

We will start by attempting the most basic model, a linear regression, as we are still learning. We will, however, get a little more sophisticated. Following are our presumptions:

• The linear regression parameters ( α and ?) are particular to each patient. So, we will be able to anticipate the line(s) for each patient and, as a result, his FVC in any week by inferring the appropriate parameters.
• These variables are not entirely independent from one another, though. All patients are governed by a fundamental model.
• Both have different means and variances and are regularly distributed.
• The baseline measure (baseline week, FVC, and Percent), as well as the patient's age, sex, and smoking status, determine these means and variations.
• We'll go even more sophisticated in this case by supposing that the parameters are also functions of latent variables discovered from the CT scans. It will happen later, though.

Our model is represented by the Bayesian network shown below: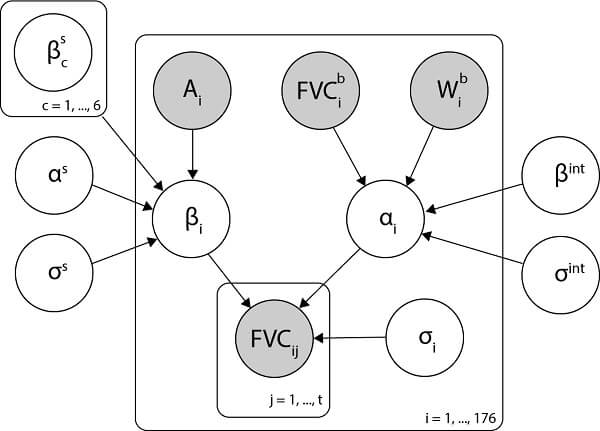

The logic behind this Model:

• FVC_ij is the observed variable we are interested in. At any week j, -12≤j≤133, the FVC of patient is presumed to be normally distributed with mean α_i+β_i i and σ_i²(the confidence asked).
• α_i, the intercept of the decline function for each patient i, logically is a function of FVC_i^b (the baseline measurement for patient i ) and ω_i^b (the week when the baseline FVC was measured). We assume it is normally distributed with mean FVC_i^b+ω_i^b β^int and variance σ^int.
• β_i, the slope of the decline function for each patient i, logically is a function of A_i (patient's age), sex, and smoking status. We assume it is normally distributed with mean α^s+A_i β_c^s with variance σ^s. We considered six different β_c^s: for women who currently smoke, men who currently smoke, women ex-smokers, men ex-smokers, women who never smoked, and men who never smoked.
• For now, to simplify, we left the Percent random variable out. We will include it in a second version.
• Finally, we know nothing about the priors β^int, α^s,σ^{i,σint, and σs. We will model the first two as normals and the last three as half-normals.}

Mathematically Model Specification: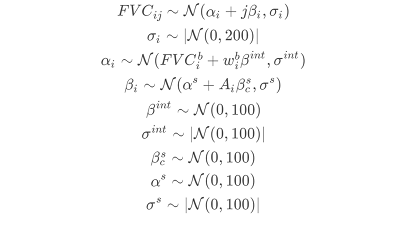

Simple Data Pre-processing

Output: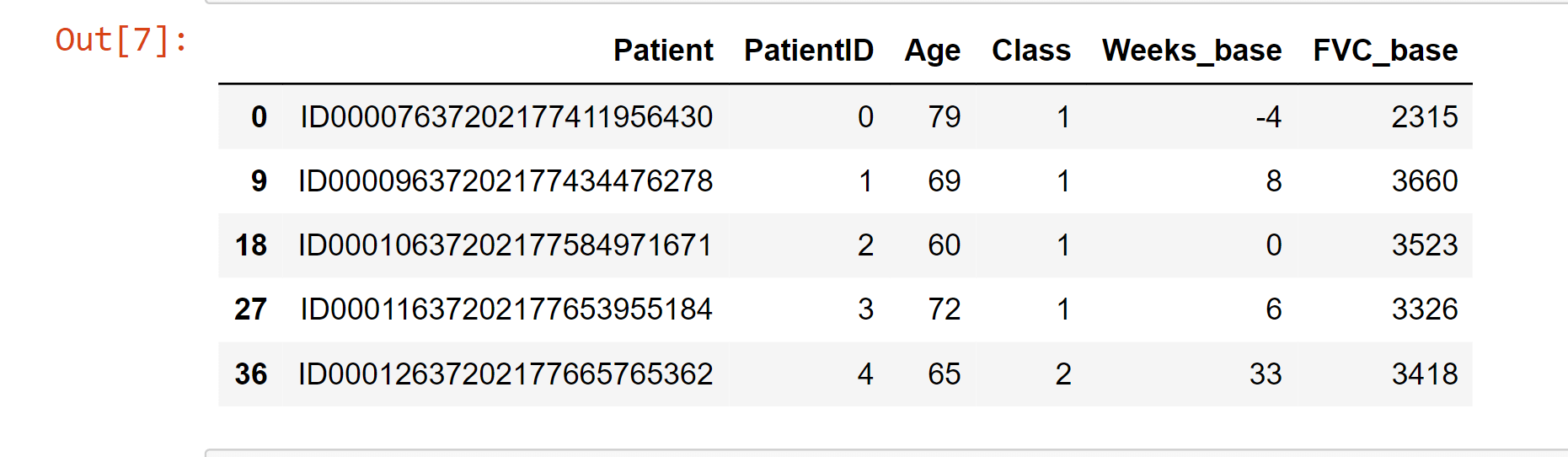

Output: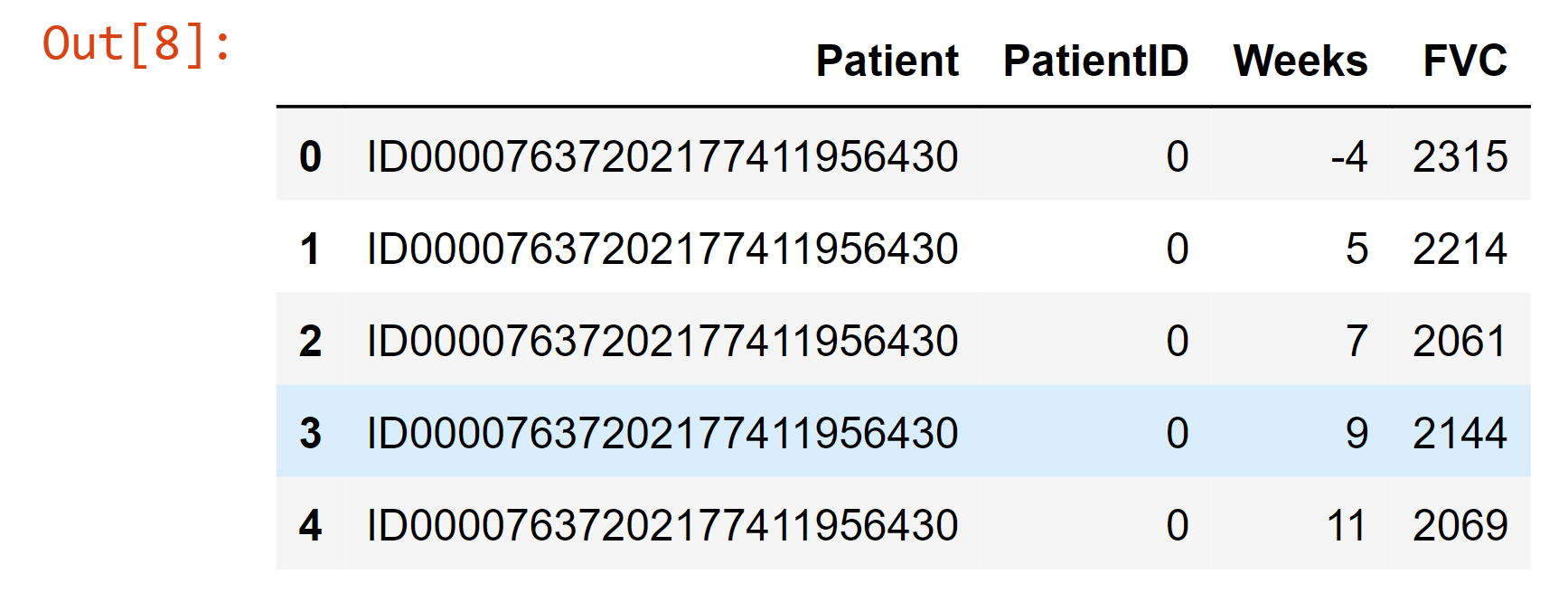

Modeling in PyMC3

Fit the model

Output:

We just sampled 4000 distinct models that account for the data.

Check the model

Let's have a look at the generative model we developed.

Output:

It appears that our model has learned unique alphas and betas for each patient.

Checking some patients

ArviZ, an extremely potent visualization tool, is included with PyMC3. Nonetheless, we make use of Seaborn and Matplotlib.

Output: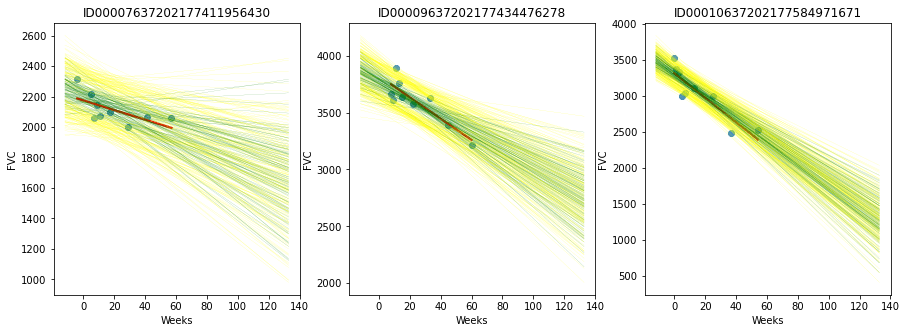

100 of the 4000 unique models that each patient possesses is plotted here. The fitted regression line is shown in green, while the standard deviation is shown in yellow. Let's put it all together!

(Iterate and) Use the model

Let's use our generative model now.

Simple Data Pre-processing

Output: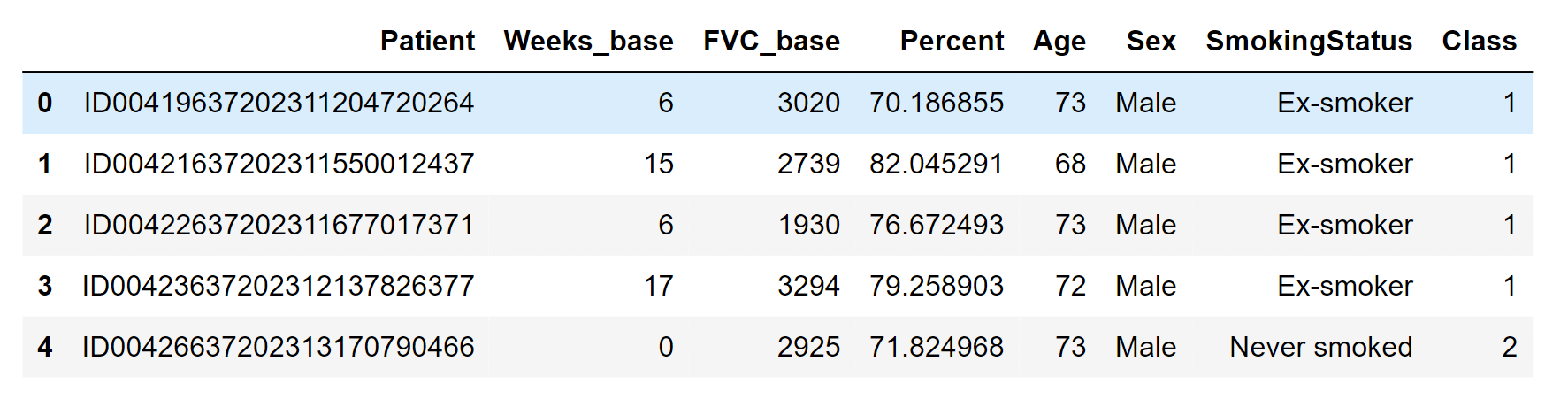

Output: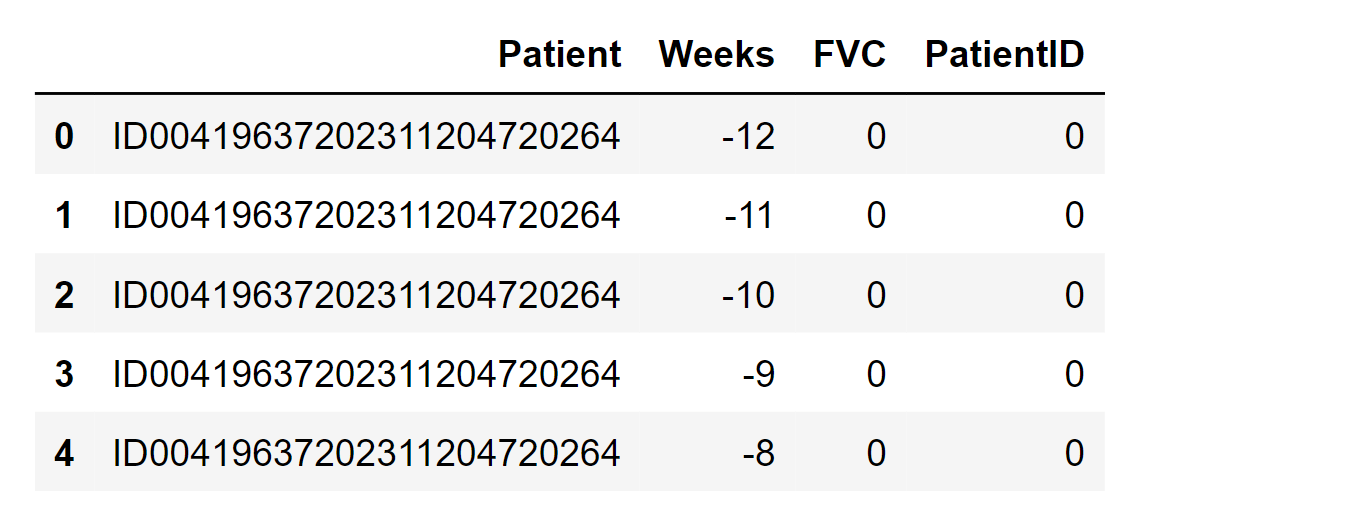

Posterior Prediction

PyMC3 offers two methods for making predictions on held-out data that has not yet been viewed. Using theano.shared variables is part of the initial step. We only need to write 4-5 lines of code to complete it. We tested it, and while it did work flawlessly, we will also utilise the second strategy for greater comprehension.

Although it's a tiny bit longer than the 4-5 lines of code, We find it to be far more instructive. Developers of PyMC3 explain the concept in this response from Luciano Paz. Using the distributions for the parameters learnt on the first model as priors, we will build a second model to predict FVCs on hold-out data. We continuously update our models in accordance with the Bayesian methodology as we gather new data.

Output:

Output: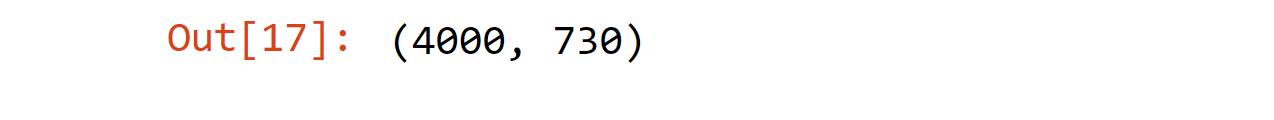

Let's go! 4000 forecasts for every point!

Generating Final Predictions

Output: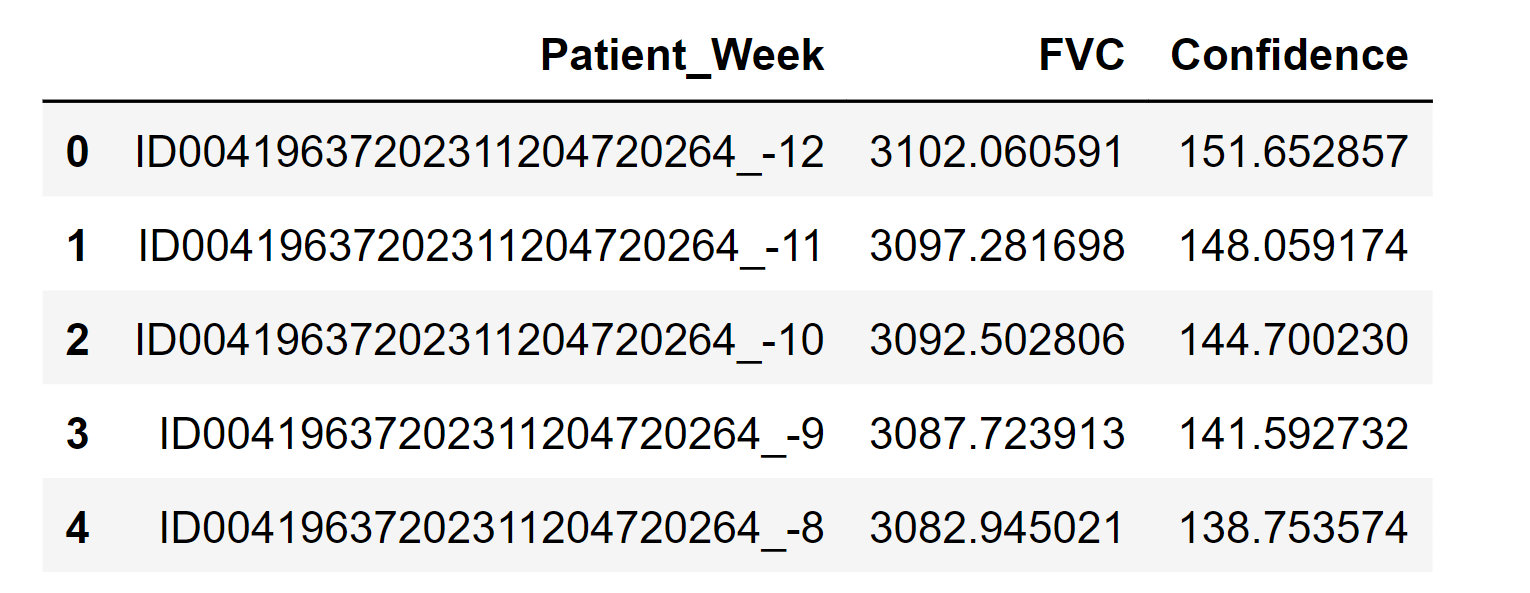

Note: We generate the final prediction so that we can submit it to the competition for evaluation.

Conclusion

At its core, a probabilistic model is simply a model that incorporates uncertainty. In machine learning, this often involves representing the relationships between different variables in a system using probability distributions. For example, in a classification task, a probabilistic model might represent the probability of a particular input belonging to each possible class.