Gaussian Discriminant Analysis

There are two types of Supervised Learning algorithms are used in Machine Learning for classification.

1. Discriminative Learning Algorithms
2. Generative Learning Algorithms

Logistic Regression, Perceptron, and other Discriminative Learning Algorithms are examples of discriminative learning algorithms. These algorithms attempt to determine a boundary between classes in the learning process. A Discriminative Learning Algorithm might be used to solve a classification problem that will determine if a patient has malaria. The boundary is then checked to see if the new example falls on the boundary, P(y|X), i.e., Given a feature set X, what is its probability of belonging to the class "y".

Generative Learning Algorithms, on the other hand, take a different approach. They try to capture each class distribution separately rather than finding a boundary between classes. A Generative Learning Algorithm, as mentioned, will examine the distribution of infected and healthy patients separately. It will then attempt to learn each distribution's features individually. When a new example is presented, it will be compared to both distributions, and the class that it most closely resembles will be assigned, P(X|y) for a given P(y) here, P(y) is known as a class prior.

These Bayes Theory predictions are used to predict generative learning algorithms: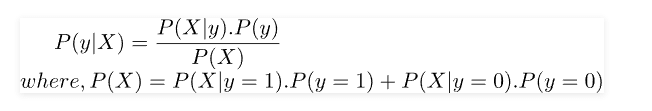

By analysing only, the numbers of P(X|y) as well as P(y) in the specific class, we can determine P(y), i.e., considering the characteristics of a sample, how likely is it that it belongs to class "y".

Gaussian Discriminant Analysis is a Generative Learning Algorithm that aims to determine the distribution of every class. It attempts to create the Gaussian distribution to each category of data in a separate way. The likelihood of an outcome in the case using an algorithm known as the Generative learning algorithm is very high if it is close to the centre of the contour, which corresponds to its class. It diminishes when we move away from the middle of the contour. Below are images that illustrate the differences between Discriminative as well as Generative Learning Algorithms.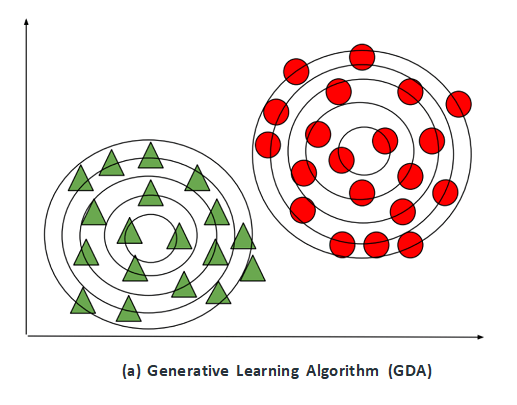

Let's take a look at the case of a classification binary problem in which all datasets have IID (Independently and identically distributed). To determine P(X|y), we can use Multivariate Gaussian Distribution to calculate a probability density equation for every particular class. In order to determine P(y) or the class prior for each class, we can make use of the Bernoulli distribution since all sample data used in binary classification could be 0 or 1.

So the probability distribution, as well as a class prior to a sample, could be determined using the general model of Gaussian and Bernoulli distributions: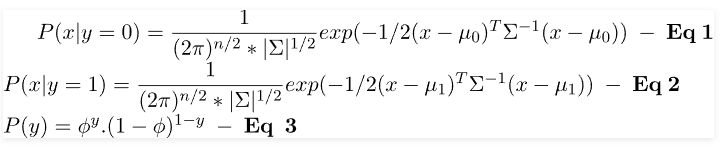

To understand the probability distributions in terms of the above parameters, we can formulate the likelihood formula, which is the product of the probability distribution as well as the class before every data sample (Taking the probability distribution as a product is reasonable since all samples of data are considered IID).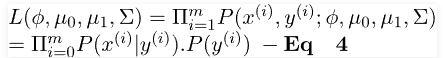

In accordance with the principle of Likelihood estimation, we need to select the parameters so as to increase the probability function, as shown in Equation 4. Instead of maximizing the Likelihood Function, we can boost the Log-Likelihood Function, a strict growing function.

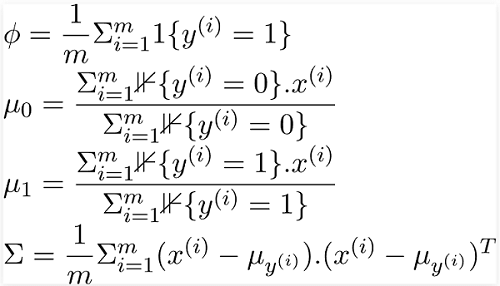
In the above equations, "1{condition}" is the indicator function that returns 1 if this condition holds; otherwise returns zero. For instance, 1{y = 1} returns 1 only if the class of the data sample is 1. Otherwise, it returns 0 in the same way, and similarly, in the event of 1{y = 0}, it will return 1 only if the class of the sample is 0. Otherwise, it returns 0.

The parameters derived can be used in equations 1, 2, and 3, to discover the probability distribution and class before the entire data samples. The values calculated can be further multiplied in order to determine the Likelihood function, as shown in Equation 4. As previously mentioned, it is the probability function, i.e., P(X|y). P(y) is integrated into the Bayes formula to calculate P(y|X) (i.e., determine the type 'y' of a data sample for the specified characteristics ' X').

Thus, Gaussian Discriminant Analysis works extremely well with a limited volume of data (say several thousand examples) and may be more robust than Logistic Regression if our fundamental assumptions regarding data distribution are correct.