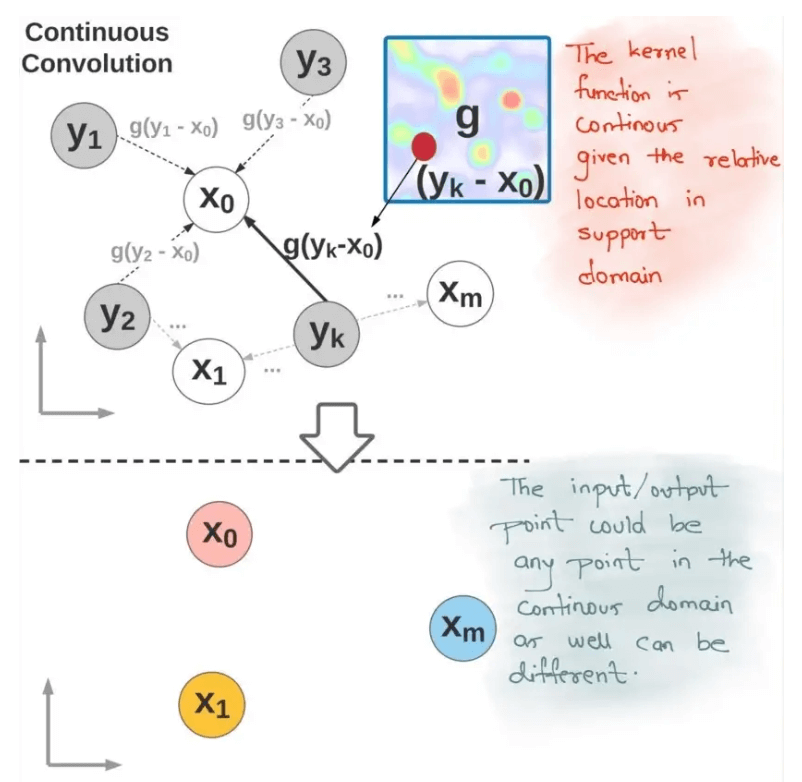
Deep Parametric Continuous Convolutional Neural Network

Parametric continuous convolution is an innovative learnable operator that works with non-grid structured data. The main concept is to utilize parameterized kernel functions that cover the entire continuous vector space. Researchers from Uber Advanced Technologies Group proposed Deep Parametric Continuous Kernel convolution. The simple CNN architecture assumes a grid-like layout and uses discrete convolution as its core building component, which is the driving force behind this paper. This makes it difficult for them to carry out precise convolution for numerous real-world applications. As a result, they suggest a convolution technique known as Parametric Continuous Convolution.

Parametric Continuous Convolution:

Using parameterized kernels that cover the entire continuous vector space, parametric continuous convolution is a learnable operator that functions on non-grid organized data. If the support structure is computable, it can handle any data structure. By using Monte Carlo sampling, the continuous convolution operator can be roughly compared to a discrete: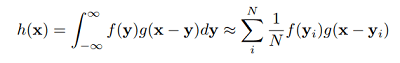

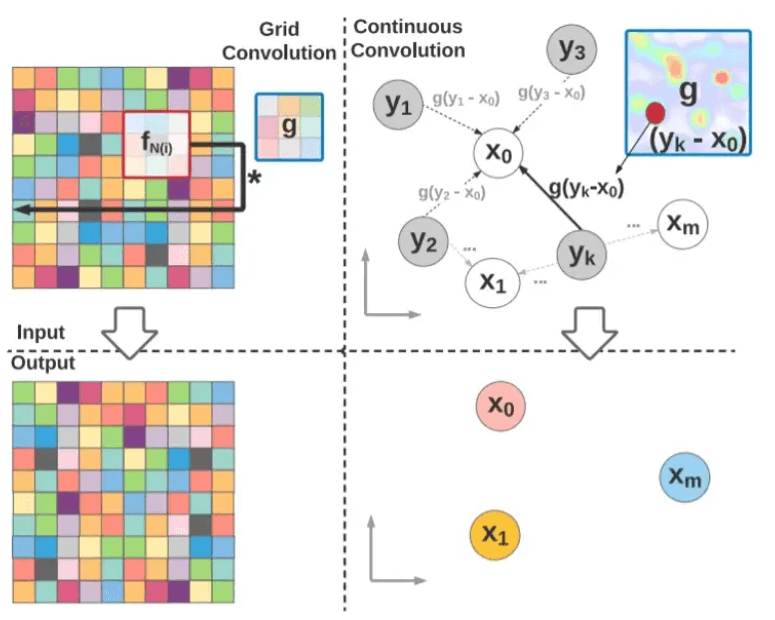
But how do we create the continuous convolution kernel function g, which is parameterized to give each point in the support domain a value? (Kernel weights). For continuous convolution, such parameterization is impossible because the function g will be specified across an unlimited number of points.

Multi-layer perceptrons (MLPs) are expressive and capable of approximating continuous functions. Therefore the solution to the problem is to model g using continuous parametric functions.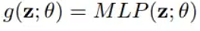

The kernel function g(z), specified by a finite set of parameters, encompasses the entire continuous support domain.

Continuous Parametric Convolution Layer:

The parametric continuous convolution layer can have varied input and output. Each convolution layer's input consists of the following three components:

• Feature vector input (F)
• The corresponding place in the support domain (S = Yj)
• Location of the output domain (0 = Xi)

We assess the kernel function g(Yj - Xi; ) for each layer for all Xi in S and all Yj in O. The output feature is finally determined as follows: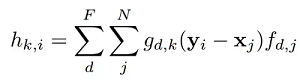

where,

• N: the number of input points
• M: the total output points.
• D: The dimension of the support domain is D.
• F: Dimension of the output feature
• 0: The feature dimension entered is 0.

Architecture: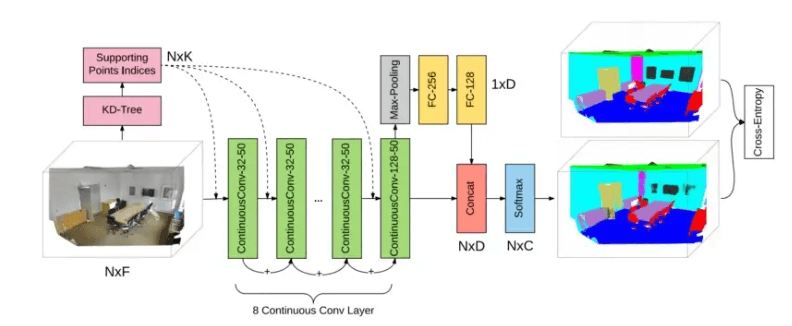

The input feature and its position in the support domain are provided to the network as input. We may add batch normalization, non-linearities, and the remaining connection between layers, which was essential for assisting convergence, to the traditional CNN architecture. Information can be gathered across the support domain by using pooling.

Backpropagation can be used to train the network because all the blocks are differentiable.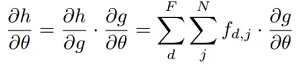

Enforcing Locality Convolution that is ongoing.

To maintain locality, the conventional convolution kernel has a small size. Limiting the influence of the function g to points near x can also be enforced via parametric continuous convolution. so,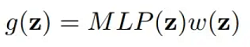

where K-nearest neighbors (kNN) or points inside a set radius are the only points we can preserve non-zero kernel values for in the modulating window (w) (Ball-point).

Analysis: