Entropy in Machine Learning

We are living in a technology world, and somewhere everything is related to technology. Machine Learning is also the most popular technology in the computer science world that enables the computer to learn automatically from past experiences.

Also, Machine Learning is so much demanded in the IT world that most companies want highly skilled machine learning engineers and data scientists for their business. Machine Learning contains lots of algorithms and concepts that solve complex problems easily, and one of them is entropy in Machine Learning. Almost everyone must have heard the Entropy word once during their school or college days in physics and chemistry. The base of entropy comes from physics, where it is defined as the measurement of disorder, randomness, unpredictability, or impurity in the system. In this article, we will discuss what entropy is in Machine Learning and why entropy is needed in Machine Learning. So let's start with a quick introduction to the entropy in Machine Learning.

Introduction to Entropy in Machine Learning

Entropy is defined as the randomness or measuring the disorder of the information being processed in Machine Learning. Further, in other words, we can say that entropy is the machine learning metric that measures the unpredictability or impurity in the system.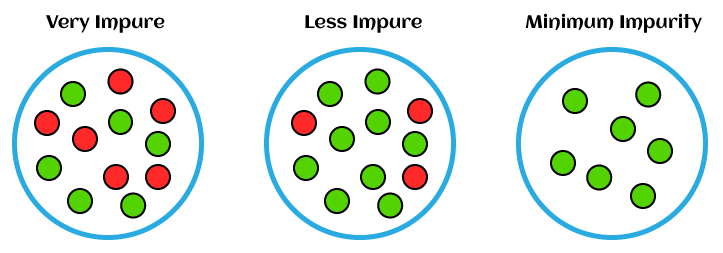

When information is processed in the system, then every piece of information has a specific value to make and can be used to draw conclusions from it. So if it is easier to draw a valuable conclusion from a piece of information, then entropy will be lower in Machine Learning, or if entropy is higher, then it will be difficult to draw any conclusion from that piece of information.

Entropy is a useful tool in machine learning to understand various concepts such as feature selection, building decision trees, and fitting classification models, etc. Being a machine learning engineer and professional data scientist, you must have in-depth knowledge of entropy in machine learning.

What is Entropy in Machine Learning

Entropy is the measurement of disorder or impurities in the information processed in machine learning. It determines how a decision tree chooses to split data.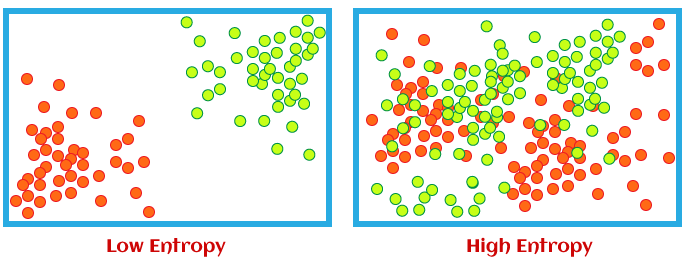

We can understand the term entropy with any simple example: flipping a coin. When we flip a coin, then there can be two outcomes. However, it is difficult to conclude what would be the exact outcome while flipping a coin because there is no direct relation between flipping a coin and its outcomes. There is a 50% probability of both outcomes; then, in such scenarios, entropy would be high. This is the essence of entropy in machine learning.

Mathematical Formula for Entropy

Consider a data set having a total number of N classes, then the entropy (E) can be determined with the formula below:

Where;

P_i = Probability of randomly selecting an example in class I;

Entropy always lies between 0 and 1, however depending on the number of classes in the dataset, it can be greater than 1. But the high value of

Let's understand it with an example where we have a dataset having three colors of fruits as red, green, and yellow. Suppose we have 2 red, 2 green, and 4 yellow observations throughout the dataset. Then as per the above equation:

E=−(prlog2pr+pplog2pp+pylog2py)

Where;

P_r = Probability of choosing red fruits;

P_g = Probability of choosing green fruits and;

P_y = Probability of choosing yellow fruits.

P_r = 2/8 =1/4 [As only 2 out of 8 datasets represents red fruits]

P_g = 2/8 =1/4 [As only 2 out of 8 datasets represents green fruits]

P_y = 4/8 = 1/2 [As only 4 out of 8 datasets represents yellow fruits]

Now our final equation will be such as;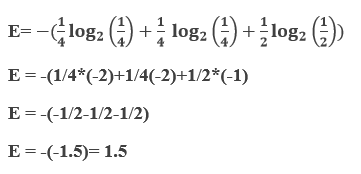

So, entropy will be 1.5.

Let's consider a case when all observations belong to the same class; then entropy will always be 0.

E=−(1log21)

= 0

When entropy becomes 0, then the dataset has no impurity. Datasets with 0 impurities are not useful for learning. Further, if the entropy is 1, then this kind of dataset is good for learning.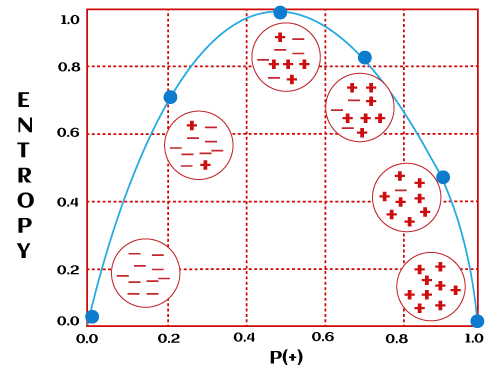

What is a Decision Tree in Machine Learning?

A decision tree is defined as the supervised learning algorithm used for classification as well as regression problems. However, it is primarily used for solving classification problems. Its structure is similar to a tree where internal nodes represent the features of the dataset, branches of the tree represent the decision rules, and leaf nodes as an outcome.

Decision trees are used to predict an outcome based on historical data. The decision tree works on the sequence of 'if-then-else' statements and a root which is our initial problem to solve.

Terminologies used in Decision Tree: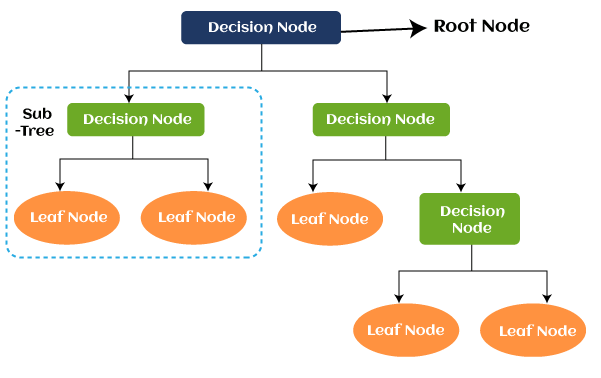

Leaf Node: Leaf node is defined as the output of decision nodes, but if they do not contain any branch, it means the tree cannot be segregated further from this node.

Root Node: As the name suggests, a root node is the origin point of any decision tree. It contains the entire data set, which gets divided further into two or more sub-sets. This node includes multiple branches and is used to make any decision in classification problems.

Splitting: It is a process that divides the root node into multiple sub-nodes under some defined conditions.

Branches: Branches are formed by splitting the root node or decision node.

Pruning: Pruning is defined as the process of removing unwanted branches from the tree.

Parent Node: The root node in a decision tree is called the parent node.

Child Node: Except for the root node, all other nodes are called child nodes in the decision tree.

Use of Entropy in Decision Tree

In decision trees, heterogeneity in the leaf node can be reduced by using the cost function. At the root level, the entropy of the target column can be determined by the Shannon formula, in which Mr. Shannon has described the weighted entropy as the entropy calculated for the target column at every branch. However, in simple words, you can understand the weighted entropy as the individual weight of each attribute. Further, weights are considered as the probability of each class individually. The more the decrease in entropy, the more information is gained.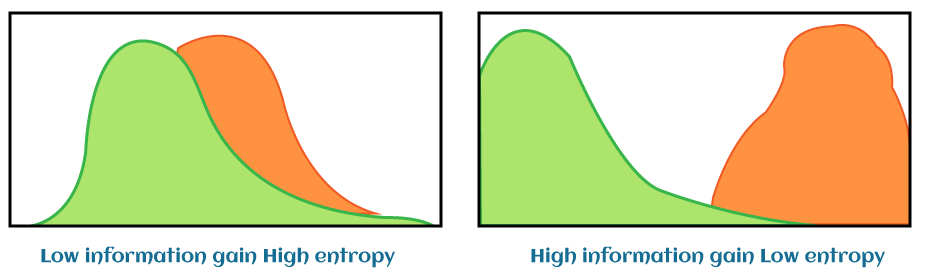

What is the information gain in Entropy?

Information gain is defined as the pattern observed in the dataset and reduction in the entropy.

Mathematically, information gain can be expressed with the below formula:

Information Gain = (Entropy of parent node)-(Entropy of child node)

Note: Information gain is calculated as 1-Entropy.

Let's understand it with an example having three scenarios as follows:

Let's say we have a tree with a total of four values at the root node that is split into the first level having one value in one branch (say, Branch 1) and three values in the other branch (Branch 2). The entropy at the root node is 1.

Now, to compute the entropy at the child node 1, the weights are taken as ? for Branch 1 and ? for Branch 2 and are calculated using Shannon's entropy formula. As we had seen above, the entropy for child node 2 is zero because there is only one value in that child node, meaning there is no uncertainty, and hence, the heterogeneity is not present.

H(X) = - [(1/3 * log2 (1/3)) + (2/3 * log2 (2/3))] = 0.9184

The information gain for the above case is the reduction in the weighted average of the entropy.

Information Gain = 1 - ( ¾ * 0.9184) - (¼ *0) = 0.3112

The more the entropy is removed, the greater the information gain. The higher the information gain, the better the split.

How to build decision trees using information gain:

After understanding the concept of information gain and entropy individually now, we can easily build a decision tree. See steps to build a decision tree using information gain:

1. An attribute with the highest information gain from a set should be selected as the parent (root) node. From the image below, it is attributed A.
   
2. Build child nodes for every value of attribute A.
3. Repeat iteratively until you finish constructing the whole tree.

Advantages of the Decision Tree:

• A decision tree can be easily understandable as it follows the same process of human thinking while making any decision.
• It is used to solve any decision-related problem in machine learning.
• It helps in finding out all the possible outcomes for a problem.
• There is less requirement for data cleaning compared to other algorithms.