Linear Discriminant Analysis (LDA) in Machine Learning

Linear Discriminant Analysis (LDA) is one of the commonly used dimensionality reduction techniques in machine learning to solve more than two-class classification problems. It is also known as Normal Discriminant Analysis (NDA) or Discriminant Function Analysis (DFA).

This can be used to project the features of higher dimensional space into lower-dimensional space in order to reduce resources and dimensional costs. In this topic, "Linear Discriminant Analysis (LDA) in machine learning”, we will discuss the LDA algorithm for classification predictive modeling problems, limitation of logistic regression, representation of linear Discriminant analysis model, how to make a prediction using LDA, how to prepare data for LDA, extensions to LDA and much more. So, let's start with a quick introduction to Linear Discriminant Analysis (LDA) in machine learning.

Note: Before starting this topic, it is recommended to learn the basics of Logistic Regression algorithms and a basic understanding of classification problems in machine learning as a prerequisite

What is Linear Discriminant Analysis (LDA)?

Although the logistic regression algorithm is limited to only two-class, linear Discriminant analysis is applicable for more than two classes of classification problems.

Linear Discriminant analysis is one of the most popular dimensionality reduction techniques used for supervised classification problems in machine learning. It is also considered a pre-processing step for modeling differences in ML and applications of pattern classification.

Whenever there is a requirement to separate two or more classes having multiple features efficiently, the Linear Discriminant Analysis model is considered the most common technique to solve such classification problems. For e.g., if we have two classes with multiple features and need to separate them efficiently. When we classify them using a single feature, then it may show overlapping.

To overcome the overlapping issue in the classification process, we must increase the number of features regularly.

Example:

Let's assume we have to classify two different classes having two sets of data points in a 2-dimensional plane as shown below image: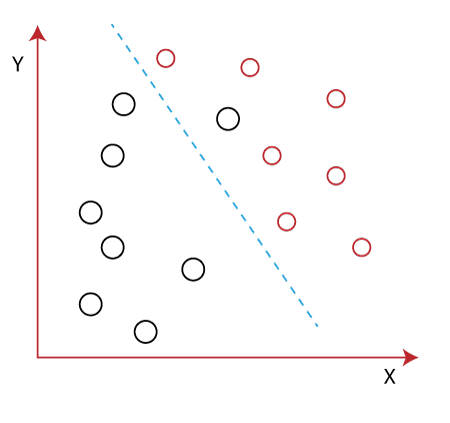

However, it is impossible to draw a straight line in a 2-d plane that can separate these data points efficiently but using linear Discriminant analysis; we can dimensionally reduce the 2-D plane into the 1-D plane. Using this technique, we can also maximize the separability between multiple classes.

How Linear Discriminant Analysis (LDA) works?

Linear Discriminant analysis is used as a dimensionality reduction technique in machine learning, using which we can easily transform a 2-D and 3-D graph into a 1-dimensional plane.

Let's consider an example where we have two classes in a 2-D plane having an X-Y axis, and we need to classify them efficiently. As we have already seen in the above example that LDA enables us to draw a straight line that can completely separate the two classes of the data points. Here, LDA uses an X-Y axis to create a new axis by separating them using a straight line and projecting data onto a new axis.

Hence, we can maximize the separation between these classes and reduce the 2-D plane into 1-D.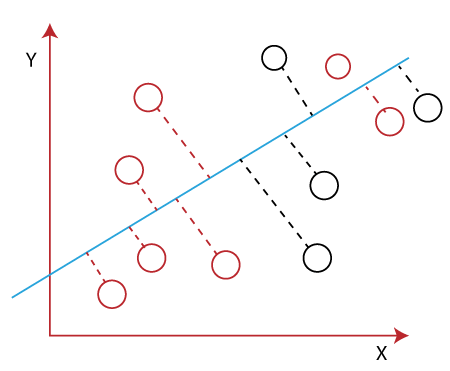

To create a new axis, Linear Discriminant Analysis uses the following criteria:

• It maximizes the distance between means of two classes.
• It minimizes the variance within the individual class.

Using the above two conditions, LDA generates a new axis in such a way that it can maximize the distance between the means of the two classes and minimizes the variation within each class.

In other words, we can say that the new axis will increase the separation between the data points of the two classes and plot them onto the new axis.

Why LDA?

• Logistic Regression is one of the most popular classification algorithms that perform well for binary classification but falls short in the case of multiple classification problems with well-separated classes. At the same time, LDA handles these quite efficiently.
• LDA can also be used in data pre-processing to reduce the number of features, just as PCA, which reduces the computing cost significantly.
• LDA is also used in face detection algorithms. In Fisherfaces, LDA is used to extract useful data from different faces. Coupled with eigenfaces, it produces effective results.

Drawbacks of Linear Discriminant Analysis (LDA)

Although, LDA is specifically used to solve supervised classification problems for two or more classes which are not possible using logistic regression in machine learning. But LDA also fails in some cases where the Mean of the distributions is shared. In this case, LDA fails to create a new axis that makes both the classes linearly separable.

To overcome such problems, we use non-linear Discriminant analysis in machine learning.

Extension to Linear Discriminant Analysis (LDA)

Linear Discriminant analysis is one of the most simple and effective methods to solve classification problems in machine learning. It has so many extensions and variations as follows:

1. Quadratic Discriminant Analysis (QDA): For multiple input variables, each class deploys its own estimate of variance.
2. Flexible Discriminant Analysis (FDA): it is used when there are non-linear groups of inputs are used, such as splines.
3. Flexible Discriminant Analysis (FDA): This uses regularization in the estimate of the variance (actually covariance) and hence moderates the influence of different variables on LDA.

Real-world Applications of LDA

Some of the common real-world applications of Linear discriminant Analysis are given below:

• Face Recognition
  Face recognition is the popular application of computer vision, where each face is represented as the combination of a number of pixel values. In this case, LDA is used to minimize the number of features to a manageable number before going through the classification process. It generates a new template in which each dimension consists of a linear combination of pixel values. If a linear combination is generated using Fisher's linear discriminant, then it is called Fisher's face.
• Medical
  In the medical field, LDA has a great application in classifying the patient disease on the basis of various parameters of patient health and the medical treatment which is going on. On such parameters, it classifies disease as mild, moderate, or severe. This classification helps the doctors in either increasing or decreasing the pace of the treatment.
• Customer Identification
  In customer identification, LDA is currently being applied. It means with the help of LDA; we can easily identify and select the features that can specify the group of customers who are likely to purchase a specific product in a shopping mall. This can be helpful when we want to identify a group of customers who mostly purchase a product in a shopping mall.
• For Predictions
  LDA can also be used for making predictions and so in decision making. For example, "will you buy this product” will give a predicted result of either one or two possible classes as a buying or not.
• In Learning
  Nowadays, robots are being trained for learning and talking to simulate human work, and it can also be considered a classification problem. In this case, LDA builds similar groups on the basis of different parameters, including pitches, frequencies, sound, tunes, etc.

Difference between Linear Discriminant Analysis and PCA

Below are some basic differences between LDA and PCA:

• PCA is an unsupervised algorithm that does not care about classes and labels and only aims to find the principal components to maximize the variance in the given dataset. At the same time, LDA is a supervised algorithm that aims to find the linear discriminants to represent the axes that maximize separation between different classes of data.
• LDA is much more suitable for multi-class classification tasks compared to PCA. However, PCA is assumed to be an as good performer for a comparatively small sample size.
• Both LDA and PCA are used as dimensionality reduction techniques, where PCA is first followed by LDA.

How to Prepare Data for LDA

Below are some suggestions that one should always consider while preparing the data to build the LDA model:

• Classification Problems: LDA is mainly applied for classification problems to classify the categorical output variable. It is suitable for both binary and multi-class classification problems.
• Gaussian Distribution: The standard LDA model applies the Gaussian Distribution of the input variables. One should review the univariate distribution of each attribute and transform them into more Gaussian-looking distributions. For e.g., use log and root for exponential distributions and Box-Cox for skewed distributions.
• Remove Outliers: It is good to firstly remove the outliers from your data because these outliers can skew the basic statistics used to separate classes in LDA, such as the mean and the standard deviation.
• Same Variance: As LDA always assumes that all the input variables have the same variance, hence it is always a better way to firstly standardize the data before implementing an LDA model. By this, the Mean will be 0, and it will have a standard deviation of 1.