Depth-wise Separable Convolutional Neural Networks

In artificial neural networks (ANNs), Convolution is a crucial mathematical procedure. Convolutional neural networks (CNNs) can categorize data using image frames and learn features. There are numerous varieties of CNNs. Depth-wise separable convolutional neural networks are one type of CNN.

These CNNs are frequently utilized for the two reasons listed below:

• Compared to standard CNNs, they have fewer parameters to change, which lessens overfitting.
• Because they use less computations and are hence more affordable computationally, they are appropriate for mobile vision applications.

Convolutional neural networks (CNN most )'s widely used convolutional layer is 2D Convolution. A novel type of convolutional layer known as Depth wise Separable convolution is used in the considerably quicker and smaller CNN architecture known as Mobile Net. Due to their compact size, these models are regarded as being extremely beneficial for implementation on embedded and mobile devices. Hence the moniker Mobile Net.

Depth-wise Convolutions :

Differences

The primary distinction between Depth wise Convolution and 2D Convolution is that Depth wise Convolution keeps each input channel independent, while 2D Convolution performs convolutions overall or multiple input channels.

Method

• The three-dimensional input tensor is divided into distinct channels.
• The input is convolved using a filter for each channel (2D)
• Each channel's output is combined to provide the output for the complete 3D tensor.

Convolutions that can be Separated in Depth:

Usually, Depthwise Separable Convolution is used in conjunction with Depthwise Convolutions. This consists of two parts: 1. Filtering (all the prior processes) and 2. Combining (combining the three color channels to create as many channels as needed; in the example below, we can see how the three channels can be combined to create a single output channel).

Why is Depthwise Separable Convolution so efficient?

• Convolutions are performed at a depth of -1x1 for all channels.
• Assume we have an input tensor with the dimensions 8x8x3.
• The size of the required output tensor is 8x8x256.

2D Convolutions

• The required multiplications are (8x8) x (5x5x3) x (256) for a total of 1,228,800.

Convolutions that can be Separable in Depth

• The required number of multiplications is:

Filtering: Due to the split into single channels, a 5x5x1 filter is needed instead of a 5x5x3 filter, and since there are three channels, a total of three 5x5x1 filters are needed.

(8x8) x (5x5x1) x (3) = 3,800

Combining: A total of 256 channels are needed, hence,

(8x8) x (1x1x3) x (256) = 49,152

3,800 + 49,152 multiplied together equals 53,952 in total.

Thus, a Depthwise Separable convolution will only need 53,952 multiplications to get the same output as a 2D convolution, which will require 1,228,800.

Finally,

1,228,800/53,952 equals 23 times fewer multiplications needed.

Because of this, Depthwise Separable convolutions have very high efficiency. These are the layers that the Mobile Net architecture has incorporated to reduce the number of computations and make them less power-hungry so that they can be used on mobile and embedded devices that lack potent graphical processing units.

How Normal Convolution works:

Consider the following input data dimensions: Df x Df x M, where M is the number of channels and Df x Df may be the size of the image (3 for an RGB image). Assume that there are N filters or kernels with Dk x Dk x M dimensions. A typical convolution operation will have an output size of Dp x Dp x N.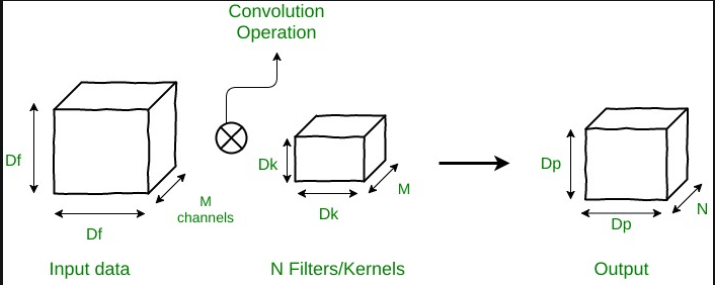

For the number of multiplications in a single convolution operation, the filter size is equal to Dk x Dk x M.

Each of the N filters slides Dp times in both the vertical and horizontal directions.

The total number of multiplications (Multiplications per Convolution) required to carry out a convolution is N x Dp x Dp x.

The total number of multiplications is N x Dp2 x Dk2 x M.

Convolutions that can be Divided By Depth

Look at separable convolutions based on Depth now. There are two operations in this process:

• Convolutions based on Depth.
• Convolutions are based on points.

1. Convolutions based on Depth.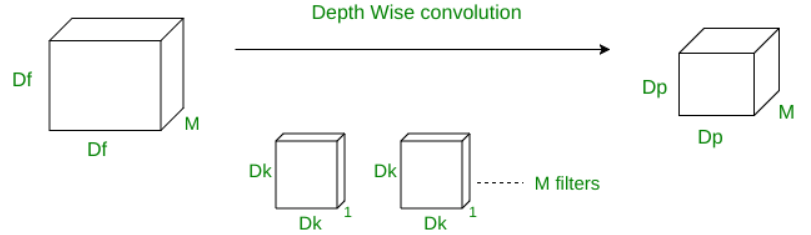

Contrary to normal CNNs, where Convolution is applied to all M channels simultaneously, the depth-wise operation only applies Convolution to one channel simultaneously. The filters/kernels used here will therefore be Dk x Dk x 1. Given that the input data has M channels, M such filters are necessary. The output will be Dp x Dp x M in size.

Cost of the Procedure:

Dk x Dk multiplications are necessary for a single convolution operation.

Since all M channels have the filter slid by DpxDp times, MxDpxDpxDkxDk is the total number of multiplications to perform depth-wise Convolution,

Multiplications total = M x Dk2 x Dp2

2. Convolutions based on points.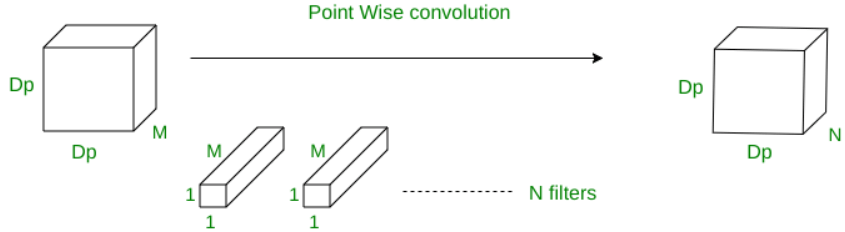

A 1 x 1 convolution procedure is used on the M channels during point-wise operation. Therefore, 1 x 1 x M will be the filter size for this operation. If N of these filters is used, the output size is Dp x Dp x N.

Cost of the Procedure:

1 x M multiplications are needed for each convolution operation.

Given that the filter is being moved by Dp times Dp,

M x Dp x Dp x is the total number of multiplications (no. of filters)

To perform point-wise Convolution,

M x Dp2 x N is the total number of multiplications.

Consequently, for optimal operation:

Total multiplications equal the sum of the depth-wise and point-wise conversions.

Total multiplications are calculated as follows: M*Dk2*Dp2+M*Dp2*N=M*Dp2*(Dk2 + n)

To perform depth-wise separable Convolution,

The total number of multiplications equals M x (Dk2 + N) x Dp2.