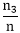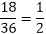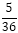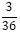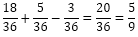Addition TheoremTheorem1: If A and B are two mutually exclusive events, then Proof: Let the n=total number of exhaustive cases Now, we have A and B two mutually exclusive events. Therefore, n1+n2 is the number of cases favorable to A or B. 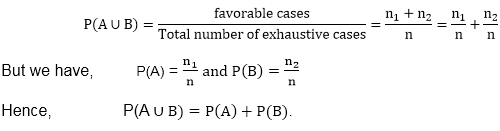
Example: Two dice are tossed once. Find the probability of getting an even number on first dice or a total of 8. Solution: An even number can be got on a die in 3 ways because any one of 2, 4, 6, can come. The other die can have any number. This can happen in 6 ways. A total of 8 can be obtained in the following cases: {(2,6),(3,5),(4,4),(5,3),(6,2)} Theorem2: If A and B are two events that are not mutually exclusive, then Proof: Let n = total number of exhaustive cases But A and B are not mutually exclusive. Therefore, A and B can occur simultaneously. So,n1+n2-n3 is the number of cases favorable to A or B. Therefore, P(A ∪B)= Hence, P(A ∪B)=P(A)+P(B)- P (A∩B). Example1: Two dice are tossed once. Find the probability of getting an even number on first dice or a total of 8. Solution: P(even number on Ist die or a total of 8) = P (even number on Ist die)+P (total of 8)= P(even number on Ist die and a total of 8) Ordered Pairs showing a total of 8 = {(6, 2), (5, 3), (4, 4), (3, 5), (2, 6)} = 5 P(even number on Ist die and total of 8) = ∴ Required Probability = Example2: Two dice are thrown. The events A, B, C, D, E, F A = getting even number on first die. Show the following: 1. A, B are a mutually exclusive event and Exhaustive Event. Solution: 
A: (2,1),(2,2),(2,3),(2,4),(2,5),(2,6) B: (1,1), (1,2),(1,3),(1,4),(1,5),(1,6) C: (1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1) D: (1,5),(1,6),(2,4),(2,5),(2,6) E: (4,6),(5,5),(5,6),(6,5),(6,6),(6,4) F: (1,2),(1,4),(1,6) 1. (A∩B) =∅ and (A∪B)=S 2. (A∩C) are not mutually exclusive 3. C∩D are a mutually exclusive but not exhaustive event. 4. C∩D=∅,D∩E=∅, C∩E=∅ are mutually exclusive and exhaustive event. 5. A'∩B' =(A∪B)' are a mutually exclusive and exhaustive event. 6. (A∩B) =∅ are a mutually exclusive
Next TopicMultiplication Theorem
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





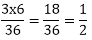
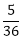
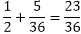
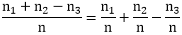
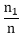 , P(B) =
, P(B) =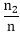 and P (A∩B)=
and P (A∩B)=