Karnaugh Maps:A Karnaugh map is a planar area subdivided into 2n equal cells each representing a point Example1: When the number of variables n = 1, the karnaugh map is like as shown in fig: 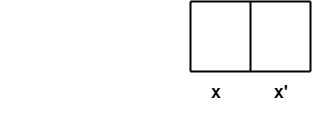 2. When the number of variables n =2, the karnaugh map is like as shown in fig: 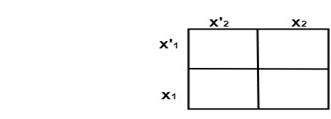 3. When the number of variables n =3, the karnaugh map is like as shown in fig: 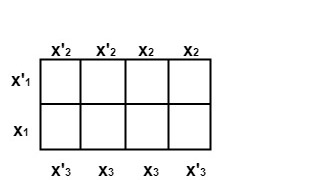
Simplification of Boolean Functions using K-Map:Boolean Functions can be simplified with k-map. It is based on the principle of combining terms in adjacent cells. Two cells are said to be adjacent if they differ in only one variable. In adjacent cells, one of the variables is the same, whereas the other variable appears in the un-complemented form in one and in the complemented form in the other cell. Minimization of SOP Form:The following algorithm can be used by which minimized expression can be obtained:
Example1: Minimize the following Boolean Expression using k-map: f(A, B) = A' B+BA Solution: First of all draw the 2-variables k-map and insert 1's in the corresponding cells as shown in fig: 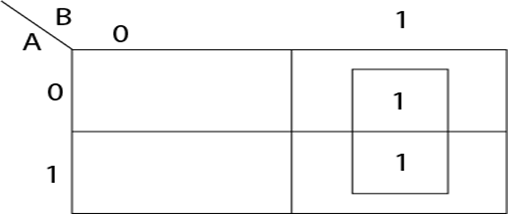
The required minimized Boolean Expression is f=B. Example2: Minimize the following Boolean Expression using k-map: AB + A' B+BA' Solution: Draw the two-variable k-map and insert 1's in the corresponding cells as shown in fig: 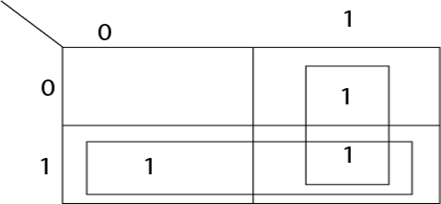
The required minimized Boolean Expression is f=A+B. Example3: Minimize the following Boolean Expression using k-map: f(A, B, C) = AB' C+A' BC+AB+A' B' C Solution: Draw the 3-variable k-map and insert 1's in the corresponding cells as shown in fig: 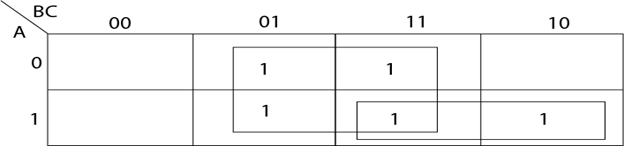
The required minimized Boolean Expression is f=AB+C' Minimisation of Boolean Functions not in Minterms/Max-terms:One way to minimize such functions is to convert them into standard forms i.e., SOP or POS, then make the k-map and obtain the minimized function. Another way is to prepare the k-map using the following algorithm directly
Example: Minimize the four variable logic function f (A, B, C, D) = A B C'D + A' BCD+A' B' C'+A' B' D'+AC'+AB' C+B' Solution: The k-map is obtained by following way (a)Enter 1 in the cell with A=1, B=1, C=0, D=1 corresponding to the min-term A B C'D (b) Enter 1 in the cell with A=0, B=1, C=1, D=1 corresponding to the min-term A' BCD (c) Enter 1's in the two cells with A=0, B=0, C=0 corresponding to the term A' B' C' (d) Enter 1's in the two cells with A=0, B=0, D=0 corresponding to the term A' B' D' (e) Enter 1's in the two cells with A=1, B=0, C=1 corresponding to the term AB' C 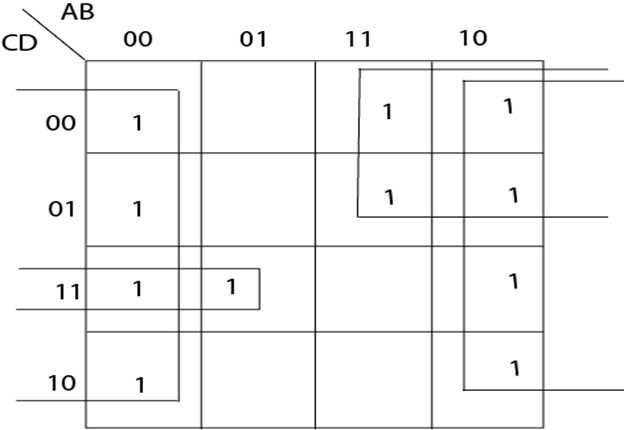
(f) Enter 1's in the four cells with A=1,C=0 corresponding to the term AC' (g) Enter 1's in the eight cells with B=0 corresponding to the term B' The minimized expression is B'+ AC'+A' CD.
Next Topic#
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




 for functions of n variables. Each variable x is used to split the area into two equal halves in a different way, i.e., one for x and other for x'. The cells corresponding to the arguments for which the function has the value 1 contains 1.
for functions of n variables. Each variable x is used to split the area into two equal halves in a different way, i.e., one for x and other for x'. The cells corresponding to the arguments for which the function has the value 1 contains 1.




