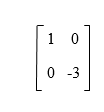Elementary Matrix in Discrete Mathematics

To learn the elementary matrix, we have to first learn about the matrix and identity matrix. After that, we can understand the concept of an elementary matrix.

Matrix

The matrix can be described as a set of numbers, which are arranged in rows and columns. These numbers are known as the entries or elements of the matrix. The square brackets are used to cover these types of elements. Suppose there is n number of rows and m number of columns. In this case, the matrix will be known as n by m matrix and can be written as "n * m". There is also a square matrix n*n, which can be described as a collection of n rows and n columns of order n.

For example: In this example, we will show a 3*3 matrix.

Solution: 3*3 matrix means there are 3 rows and 3 columns. That means total 9 elements. The 3*3 matrix is described as follows: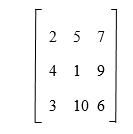

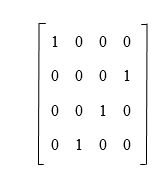
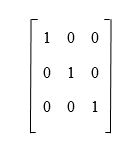
Identity Matrix

An identity matrix can be described as a square matrix of any order in which all the elements of main diagonal will contain the value 1, and all the other elements will contain the value 0. The order of an identity matrix will always be n. So we can say that the dimension of an identity matrix is n * n. That means the amount of rows and columns is always equal in this matrix. The representation of an identity matrix with different dimensions is described as below: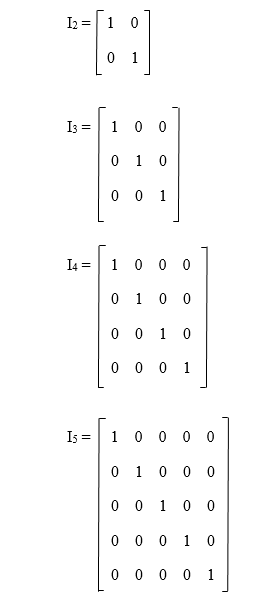

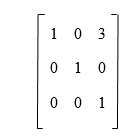
Elementary Matrix

The elementary matrix is also a type of square matrix. The elementary matrix and identity matrix are similar to each other. The only difference is that there will be one elementary rows or columns operation among three on the identity matrix in the elementary matrix. The rows operations in an elementary matrix are described as follows:

R1: Multiply the element of one row with a non-zero real number.

R2: Swapping two rows

R3: Adding of a constant k time one row to another row.

Here R1, R2, R3 are used to represent the row operations. When we apply the row operation to any matrix, then it will be known as the elementary row operations. In contrast, the columns operations in an elementary matrix are described as follows:

C1: Multiply the element of one column with a non-zero real number.

C2: Swapping two columns

C3: Adding of a constant k time one column to another column.

Here C1, C2, C3 are used to represent the column operations. When we apply the column operation to any matrix, then it will be known as the elementary column operations.

As we know that the elementary matrix is obtained from the identity matrix, and the identity matrix is always square. That's why the elementary matrix will also be square always.

Example: In this example, we will show four elementary matrices and the operations that are used to generate these matrices.

Solution:

1. The following matrix will be generated by multiplying the second row of identity matrix (I₂) by -3.
   
2. The following matrix will be generated by interchanging the second and fourth rows of identity matrix (I₄).
   
3. The following matrix will be generated by adding three times the third row of an identity matrix (I₃) to the first row.
   
4. The following matrix will be generated by multiplying the first row of an identity matrix (I₃) by 1.
   

The general linear group of the invertible matrices can be generated with the help of an elementary matrix. The elementary row operation will be represented when the elementary matrix performs the left multiplication or pre multiplication. The elementary column operation will be represented when the elementary matrix performs the right multiplication or post multiplication. The Gaussian elimination uses the elementary row operation so that it can reduce the matrix to row echelon form. The elementary row operations are also used by the gauss Jordan elimination so that they can further reduce the matrix to row echelon form. The examples of elementary row operations are described as follows:

Example: In this example, we will consider a matrix A, which is given as follows: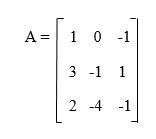

In this matrix A, we will perform the following elementary row operations like this: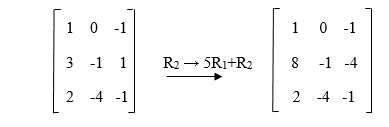

In this elementary row operation, the elementary matrix will correspond in the following way: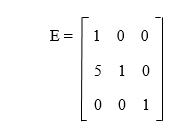

We can see that we will get the following matrix when the same elementary row operation is performed on identity matrix I. The result of multiplication of EA and the elementary row operation on matrix A is the same. The multiplication of E and A is described as follows: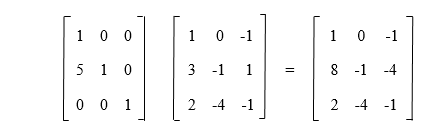

For the other elementary row operation, the same is also true. We can also perform the inverse operation on every elementary matrix. If we do the inverse of an elementary matrix, it will also be the elementary matrix. We can prove this concept by performing the reverse row operation on the identity matrix. The reverse row operations are described as follows:

• The reverse of R_i → kR_i will be R_i → 1/k R_i.
• The reverse of R_i → kR_j + R_i will be R_i → −kR_j + R_i.
• The reverse of R_i ↔ R_j will be R_i ↔ R_j.

We can perform the elementary row transformation by using the elementary matrices. It is also used to provide a constructive tool that can be used to find out the inverse matrix and also determine the LU-decomposition. The examples of elementary matrices and their inverse are described as follows, and we can check every matrix by multiplying the matrices. If the matrices are inverse, their multiplication will be I.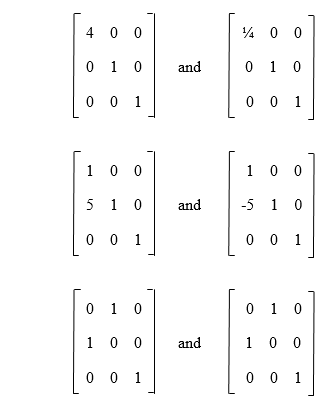

The elementary matrix has a very important fact, i.e., if matrix A is invertible, we are also able to write it as a multiplication of elementary matrices.

Properties of Elementary Matrices

All the elementary matrices are non-singular. The inverse of all non-singular elementary matrices will also be the elementary matrix. There are various properties of an elementary matrix, which are shown as follows:

1. If there is a matrix, which interchanges two rows, then the inverse of this matrix will be itself.

For example: Suppose there is a matrix, which is described as follows:

The inverse of this matrix is described as follows: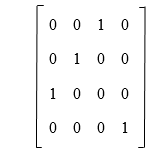

The computation of the matrix is described as follows: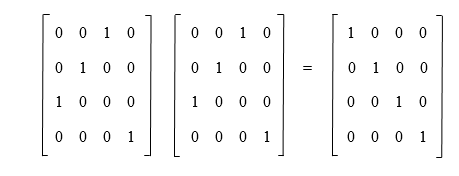

2. If there is an elementary matrix that is used to simulate (mR_i) ↔ (R_i), then the inverse of this type of matrix will also be the elementary matrix that simulates (1/m R_i) ↔ (R_i).

For example: Suppose there is a matrix, which is described as follows: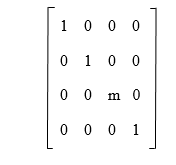

The inverse of this matrix is described as follows: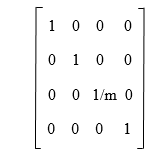

The computation of the matrix is described as follows: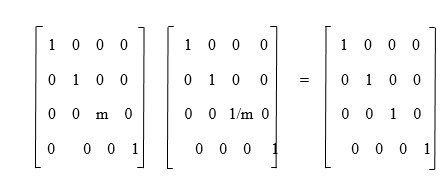

3. If there is an elementary matrix that is used to simulate (R_j + mR_i) ↔ (R_j), then the inverse of this type of matrix will also be the elementary matrix that simulates (R_j - mR_i) ↔ (R_j).

For example: Suppose there is a matrix, which is described as follows: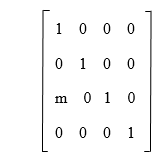

The inverse of this matrix is described as follows: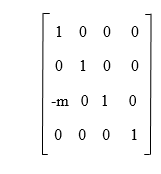

The computation of the matrix is described as follows: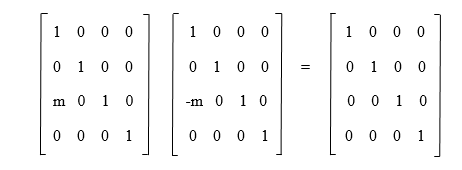

Examples of Elementary Matrix

Example 1: In this example, we have to determine that whether the given matrix A is elementary or not.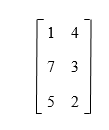

Solution: As we know, the elementary matrix is always the square matrix, and the above matrix is not a square matrix. That's why we can say that matrix A is not an elementary matrix.

Example 2: In this example, we have to determine that whether the given matrix A is an elementary matrix or not.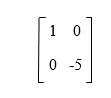

Solution: The 2*2 size of identity matrix (I₂) is described as follows: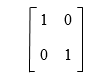

If the second row of an identity matrix (I₂) is multiplied by -3, we are able to get the above matrix A as a result. So we can say that matrix A is an elementary matrix.

Example 3: In this example, we have to determine that whether the given matrix A is an elementary matrix or not.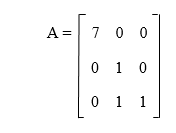

Solution: The 3*3 size of identity matrix (I₃) is described as follows: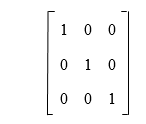

If we multiply the first row of I₃ by 7, we are able to get the following matrix: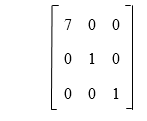

As we can see that this matrix is not equal to the given matrix A because the third row of matrix A and generated matrix are not the same. We are also not able to perform a single row or column operation so that we can get given matrix A from identity matrix I3. That's why we can say that the elementary matrix is not described by the given matrix A.