Graph Measurements in Discrete Mathematics

In this section, we will first learn about the graph to understand the measurement of graphs. After that, we will learn about the measurements of graphs that include Length of the graph, Distance between two vertices, Diameter of graph, Radius of Graph, Centre of Graph, Eccentricity of graph, Circumference of graph, and Girth of graph.

Graph:

A graph can be described as a set of vertices and edges, where vertices can be described as a set of points, and the edges can be described as a line that joins these points. Here V is used to indicate the vertices, and E is used to indicate the edges. A graph is used to contain a lot of properties, and on the basis of the structure of the graph, we can characterize the graph. In this section, we are going to learn about some basic properties of graphs, which are common in all kinds of graphs.

For example: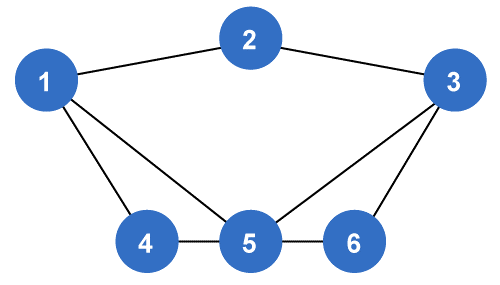

In the above graph, we have a set of vertices and edges, which are shown below:

Vertices = {1, 2, 3, 4, 5, 6}

Edges = {{1, 2}, {1, 4}, {1, 5}, {2, 3}, {3, 5}, {3, 6}, {4, 5}, {5, 6}}

Graph Measurements:

We can measure any graph with the help of some properties, which are described as follows:

1. Length of the graph
2. Distance between two vertices
3. Eccentricity of graph
4. Diameter of graph
5. Radius of Graph
6. Centre of Graph
7. Circumference of Graph
8. Girth of Graph

Now we will learn them one by one like this:

Length of Graph

We can determine the length of the graph with the help of calculating the number of edges contained in the graph. The example of calculating the length of a graph is described as follows: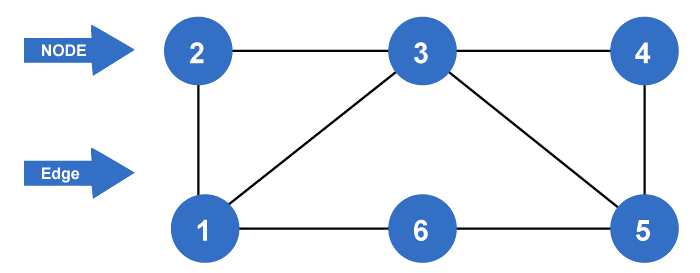

In the above graph, the number of length is 8, i.e.,

12, 23, 34, 45, 56, 61, 13, 35

The distance between two vertices

We can determine the distance between two vertices with the help of calculating the number of edges in a shortest or minimal path. It is used to provide the minimum distance between two edges. A graph has the ability to have more than one shortest path between two vertices. So if two vertices are connected by multiple paths, in this case, the shortest path will be assumed as the distance between two vertices.

Notation - d(U, V)

A graph can contain more than one number of paths between one vertex to another vertex. To determine the distance between these two vertices, we have to select only the shortest path between these two vertices.

Example:

The example of calculating distance between two vertices is described as follows: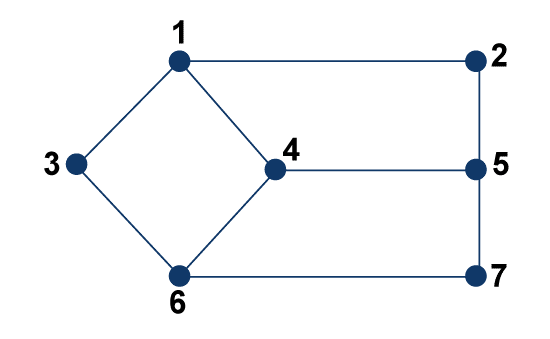

The above graph shows that the distance between vertex 4 to vertex 5 is 1. This is because there is only one edge between these two vertices. There are some other paths to reach from vertex 4 to vertex 5, which are described as follows:

1. 41, 12, 25
2. 46, 67, 75
3. 45 (This path will be considered for distance between two vertices)
4. 45, 53, 31, 12, 25
5. 41, 13, 36, 67, 75

Hence the Distance between two vertices is 1.

There is one more example of distance between two vertices, which is shown in the below graph: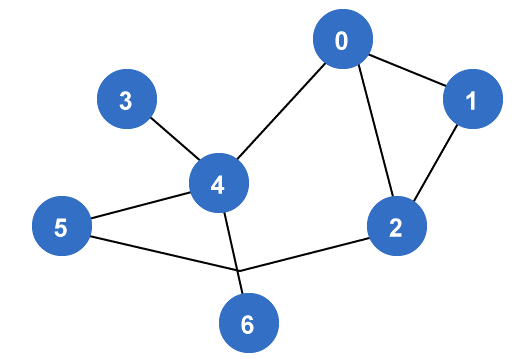

The above graph shows that the distance between vertex 1 to vertex 5 is 2. This is because there are two edges between these two vertices. There are some other paths to reach from vertex 1 to vertex 5, which are described as follows:

1. 1, 0, 4, 5
2. 1, 2, 5 (This path will be considered for distance between two vertices)
3. 1, 0, 2, 5

Hence the distance from 1 to 5 is 2.

Eccentricity of Graph

We can determine the eccentricity with the help of calculating the maximum distance between one vertex to another vertex. So the eccentricity of the vertex will be the maximum distance from a vertex to all other vertices. The symbol e(V) is used to indicate the eccentricity of a graph.

Notation - e(V)

We will first calculate the distance between a particular vertex to all other vertices, and after that, we will find the highest distance between all of the distances. This highest distance will be the eccentricity of a graph.

Example:

The example of determining the eccentricity of a graph is described as follows: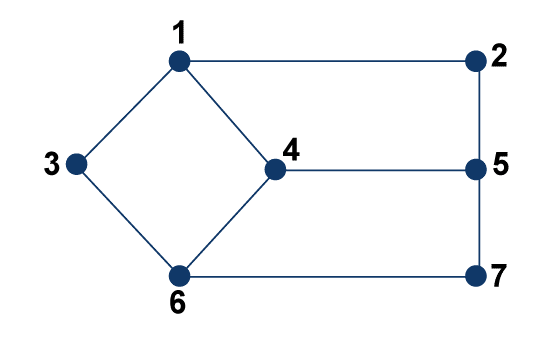

Here, the eccentricity of vertex 1 is 3.

The distance between vertex 1 to vertex 2 is 1 ('12').

The distance between vertex 1 to vertex 3 is 1 ('13').

The distance between vertex 1 to vertex 4 is 1 ('14').

The distance between vertex 1 to vertex 5 is 2 ('12'-'25') or ('14'-'45').

The distance between vertex 1 to vertex 6 is 2 ('13'-'36') or ('14'-'46').

The distance between vertex 1 to vertex 7 is 3 ('13'-'36'-'67') or ('14'-'46'-'67').

So, in conclusion, the eccentricity will be 3 because we have seen that the maximum distance between vertex 1 to vertex 7 is 3, which is the maximum distance.

In other words, the eccentricity can be shown as:

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

Hence the Eccentricity of G is 3.

There is one more example of the eccentricity of a graph, which is shown in the below graph: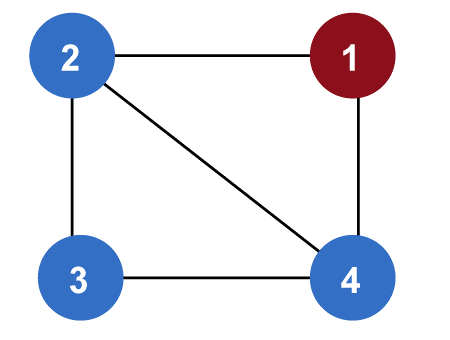

The distance between vertex 1 to vertex 1 is 0 ('11').

The distance between vertex 1 to vertex 2 is 1 ('12').

The distance between vertex 1 to vertex 3 is 2 ('12'-'23').

The distance between vertex 1 to vertex 4 is 1 ('14').

As we can see that the Maximum value of above distance is 2.

Hence Eccentricity of G is 2.

Diameter of Graph

We can determine the diameter of a graph with the help of calculating the maximum distance between pair of vertices. We will solve it with the help of determining all the paths, and then we will determine the maximum of between all these paths. In other words, the diameter of a graph can be calculated by determining the maximum eccentricity from all the vertices.

Notation -d(G)

In the graph, we will first check all the eccentricities of vertices, and after that, we will check the maximum of all those eccentricities. That maximum eccentricity will be the Diameter of a graph.

Example:

The example of calculating the diameter of a graph is described as follows: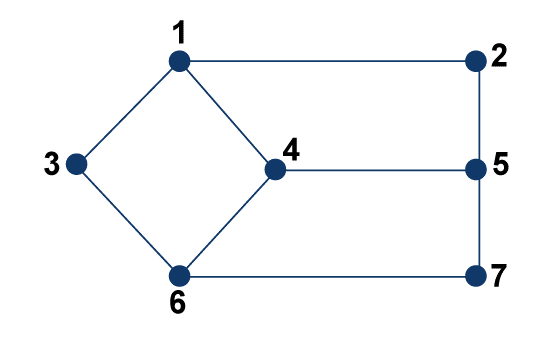

In the above graph, the diameter is 3. The reason is shown by the eccentricity of the graph, which is shown below:

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

We can see that the maximum eccentricity is 3, i.e., d(G) = 3.

Hence Diameter of G is 3.

There is one more example of diameter of a graph, which is shown in the below graph: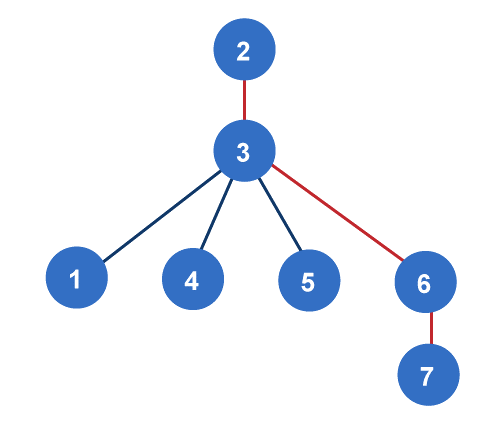

In the above graph, the radius is 3. This is because the maximum eccentricity of this graph is 3, which is shown below:

23, 36, 67

Hence, the Diameter of G is 3.

Radius of Graph

If there is a graph's diameter, only then we can calculate the radius of that graph. The radius of a graph can be described as the minimum among all the maximum distance between a particular vertex to all other vertices. The symbol r(G) is used to indicate the radius of a graph. In other words, radius of a graph can be calculated by determining the minimum eccentricity from all the vertices.

Notation - r(G)

In the graph, we will first check all the eccentricities of vertices, and after that, we will check the minimum of all those eccentricities. That minimum eccentricity will be the Radius of a graph.

Example:

The example of calculating the radius of a graph is described as follows: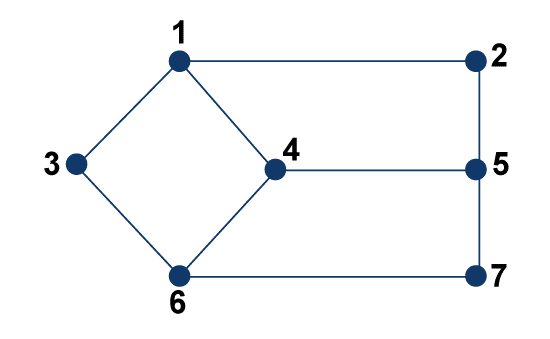

In the above graph, the radius is 2. The reason is shown by the eccentricity of the graph, which is shown below:

e(2) = 3

e(3) = 3

e(4) = 2

e(5) = 3

e(6) = 3

e(7) = 3

We can see that the minimum eccentricity for vertex 4 is 2.

Hence Radius of G is 2.

There is one more example of radius of a graph, which is shown in the below graph: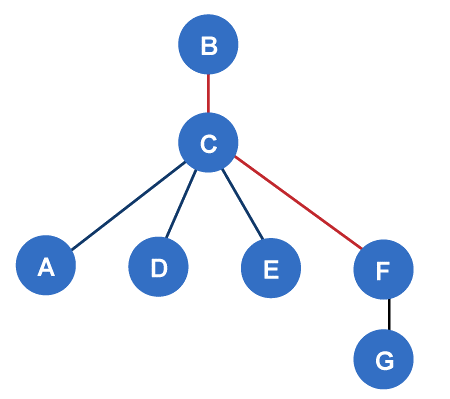

In the above graph, the Radius is 2. The reason is shown by seeing all available minimum radius, which is described below:

BC, CF

BC, CE

BC, CD

BC, CA

Hence Radius of G is 2.

Centre of Graph

We can calculate the centre of a graph if it has all the vertices which contain the eccentricity as a minimum. The centre of the graph can be described by a set of all central points of G. Here, radius and eccentricity are similar to each other. The vertex V will be known as the centre point of graph G if e(V) = r(V).

For example: If there is a school in the village centre, then the buses don't have to travel very much because it will reduce the distance. The example of determining the centre of a graph is described as follows: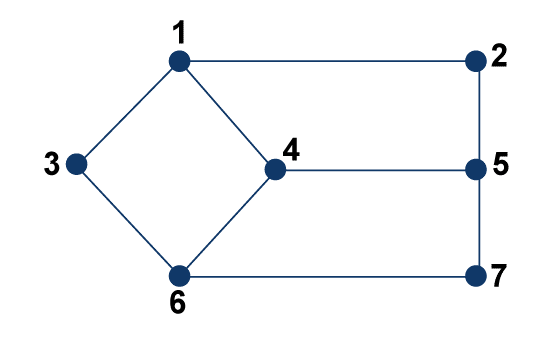

In the above graph, the Centre point is vertex 4. This is because

e(4)= r(4) = 2

There is one more example of Centre of a graph, which is shown in the below graph: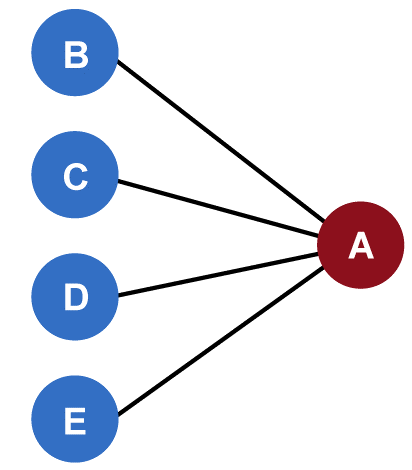

In the above graph, the centre point is A.

Circumference of a Graph

We can determine the circumference of a graph with the help of calculating the number of edges in the longest cycle of that graph. The example of determining the circumference of a graph is described as follows: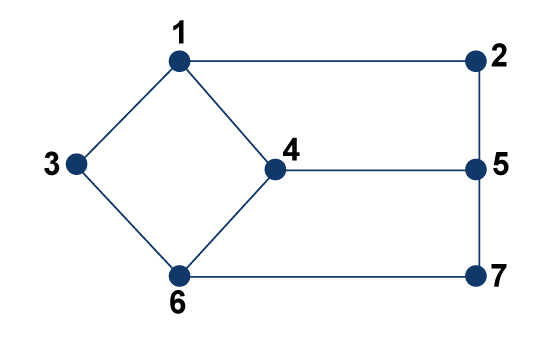

In the above graph, the circumference is 6. This is because, from the above graph, we can derive two longest cycles, i.e., 1-2-6-7-5-2-1or 1-2-6-4-5-2-1, and the longest cycle has 6 numbers of edges. So the circumference of this graph will be 6.

Girth of a Graph

We can determine the girth of a graph with the help of calculating the number of edges in the shortest path of that graph. The example of determining the girth of a graph is described as follows: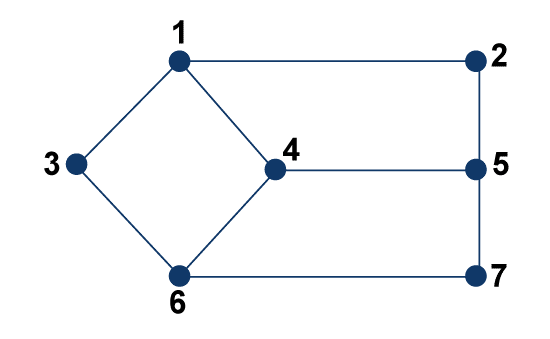

In the above graph, the Girth is 4. This is because, from the above graph, we can derive three shortest cycles, i.e., 1-3-6-4-1 or 4-6-7-5-4-1 or 1-2-5-4-1, and the shortest cycle has 4 numbers of edges. So the Girth of this graph will be 4.