Introduction to Mojette Transform

There are two ways in which the data can be roughly divided, i.e., continuous data and discrete data. The continuous data is used to contain any type of value, and discrete data is used to contain only the integer value. There is also a discrete geometry, which can be defined as a study of geometrical objects and properties of data, and those must be discrete. There are various types of applications in discrete geometry, but their main application is digital cameras and screens.

The fundamental of discrete geometry is also used by the Mojette transform. To completely understand the Mojette transform, we have to first understand the Radon transform. In 1917, the Johann radon was developed the Radon transform. It can be defined as an integral transform. To reconstruct the images, the inverse of radon transform will be used. There are various applications of radon transform, i.e., we can use it in the field of nuclear magnetic, optics, medicine, stress analysis, astronomy, and many more places.

The Mojette Transform

The Mojette transform can be described as a discrete and exact form of radon transform. A French word was used to derive the Mojette, which means beans. Discrete geometry is used by the Mojette transform so that it can store information onto discrete geometrical support. After that, this support will be projected by Mojette transform in discrete directions. The reconstruction will be possible only when it projects enough projections.

There are two types of characteristics in the Mojette transform, which is described as follows:

Mojette transform is able to reconstruct the image only with the help of additions or subtractions.
The discrete geometry is used by the transform.

The following equation is used to mathematically explain the Mojette transform like this: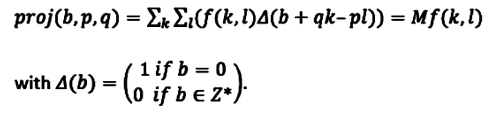

In the following image, we are going to see the various directions in Mojette transform in a 4*4 grid with 16 pixels like this: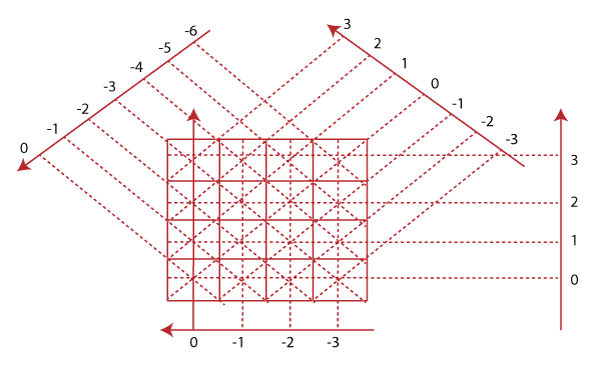

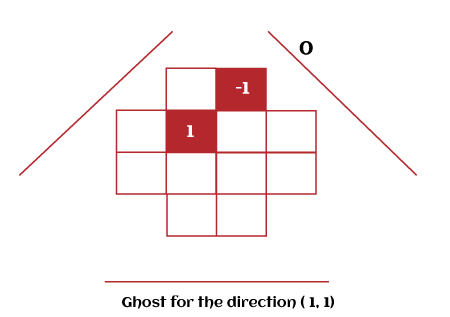
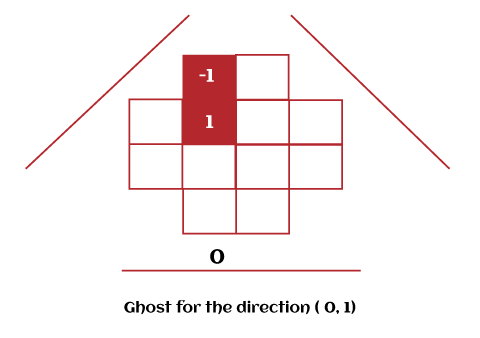
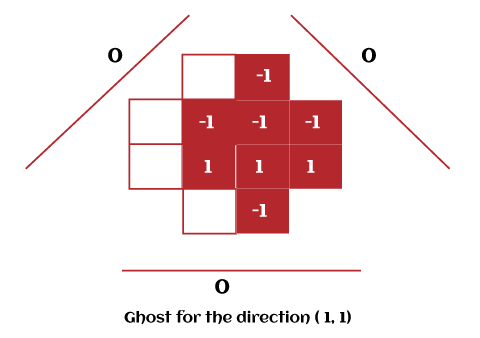
Ghosts in Discrete Tomography

There are a lot of applications in the Mojette transform, and most of them provide a unique result, but there are some cases in which unique results will not be possible. In these types of cases, we can use the phantoms or ghosts so that we can get all the possible reconstruction of images, which we can get with the help of Mojette transform. In the below image, we can see that the result of Mojette transform is not unique, so we use ghosts to get all the possible reconstructions.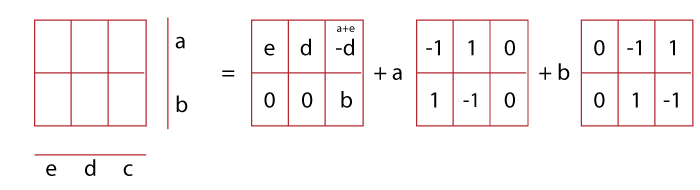

In simple words, we can define ghosts as noise or objects which we can add into the images, but we will not be able to see it in the projection of Mojette transform.

Applications of Ghosts

There are various applications of ghosts, which are described as follows:

Watermarking
Image Fingerprinting
Image Cryptography
Error correction code
Network protocol
Storage Distribution on network or disks
Distributed storage
Medical tomography

Example of Phantoms or Ghosts:

In this example, we try to introduce a ghost in direction (1, 1), which means that p = 1 and q = 1, in this case, the bin corresponds to the phantom, which shows no change, which is described in the following image:
In this example, we try to introduce a ghost in direction (0, 1), which means that p = 0 and q = 1, in this case, the bin corresponds to the phantom, which also shows no change, which is described in the following image:
The above two examples are used to show the single projection. In the below example, we will see a multi-projection ghost. The below image shows a ghost when the projections are (0, 1), (1, 1), and (-1, 1).