Cauchy's Mean Value TheoremCauchy's mean value theorem is a generalization of the normal mean value theorem. This theorem is also known as the Extended or Second Mean Value Theorem. The normal mean value theorem describes that if a function f (x) is continuous in a close interval [a, b] where (a≤x ≤b) and differentiable in the open interval [a, b] where (a < x< b), then there is at least one point x = c on this interval, given as f(b) - f (a) = f' (c) (b-a) It establishes the relationship between the derivatives of two functions and changes in these functions on a finite interval. Let's consider the function f(x) and g(x) be continuous on an interval [a,b], differentiable on (a,b), and g'(x) is not equal to 0 for all x ε (a,b). Then there is a point x = c in this interval given as 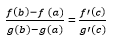
Proof of Cauchy's mean value theorem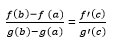
Here, the denominator in the left side of the Cauchy formula is not zero: g(b)-g(a) ≠ 0. If g(b) = g(a), then by Rolle's theorem, there is a point d ? (a,b), in which g'(d) = 0. Therefore, contradicts the hypothesis that g'(x) ≠ 0 for all x ? (a,b). Now, we apply the auxiliary function. F (x) = f (x) + λg(x) And select λ in such a way to satisfy the given condition F (a) = f (b). we get, f (a) + λg(a) = f (b) + λg(b) = f(b)-f (a) = λ[g(a)- g(b)] 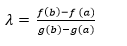
And the function F (x) exists in the form 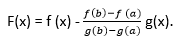
The function F (x) is continuous in the closed interval (a≤x ≤b), differentiable in the open interval (a < x< b) and takes equal vales at the endpoints of the interval. So, it satisfies all the conditions of Rolle's theorem. Then, there is a point c exist in the interval (a,b) given as F' (c) = 0. It follows that 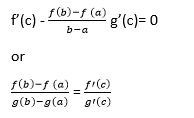
By putting g (x) = x in the given formula, we get the Lagrange formula: 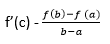
Cauchy's mean value theorem has the given geometric meaning. Consider the parametric equations give a curve ? X = f (t) and Y = g (t), where the parameter t lies in the interval [a,b]. When we change the parameter t, the point of the curve in the given figure runs from A (f (a). g(a) to B (f(b), g (b)). According to Cauchy's mean value theorem, there is a point (f(c), g(c)) on the curve ? where the tangent is parallel to the chord linking the two ends A and B of the curve. 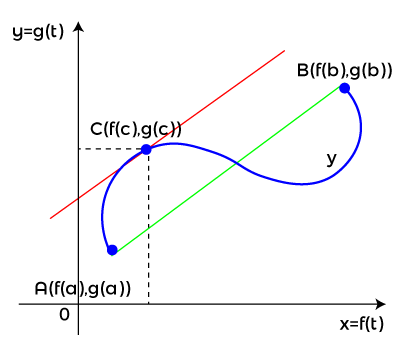
Questions Based on Cauchy's mean value theoremQuestion 1: Calculate the value of x, which satisfies the Mean Value Theorem for the following function F(x) = x2 + 2x + 2 Explanation: Given f(x) = x2 + 2x + 2 According to Mean Value theorem, 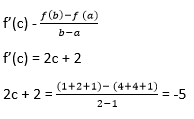
2c = -7 C = -7/2 Question 2: Calculate the value of x which satisfies the Mean Value Theorem for the following function F(x) = x2 + 4x + 7 Explanation: Given f(x) = x2 + 4x + 7 According to Mean Value theorem, 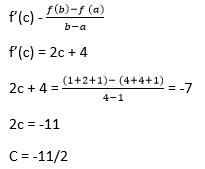
Next TopicSemantic difference between Set and Type
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










