Composition of RelationsLet A, B, and C be sets, and let R be a relation from A to B and let S be a relation from B to C. That is, R is a subset of A × B and S is a subset of B × C. Then R and S give rise to a relation from A to C indicated by R◦S and defined by: The relation R◦S is known the composition of R and S; it is sometimes denoted simply by RS. Let R is a relation on a set A, that is, R is a relation from a set A to itself. Then R◦R, the composition of R with itself, is always represented. Also, R◦R is sometimes denoted by R2. Similarly, R3 = R2◦R = R◦R◦R, and so on. Thus Rn is defined for all positive n. Example1: Let X = {4, 5, 6}, Y = {a, b, c} and Z = {l, m, n}. Consider the relation R1 from X to Y and R2 from Y to Z.
R1 = {(4, a), (4, b), (5, c), (6, a), (6, c)}
R2 = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)}
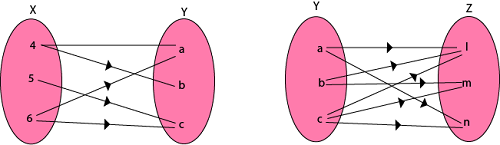
Find the composition of relation (i) R1 o R2 (ii) R1o R1-1 Solution: (i) The composition relation R1 o R2 as shown in fig: 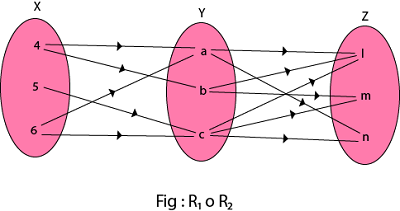
R1 o R2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)} (ii) The composition relation R1o R1-1 as shown in fig: 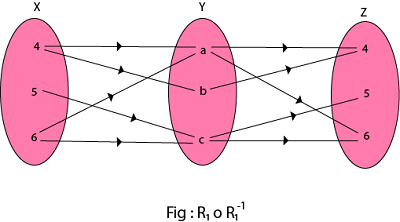
R1o R1-1 = {(4, 4), (5, 5), (5, 6), (6, 4), (6, 5), (4, 6), (6, 6)} Composition of Relations and MatricesThere is another way of finding R◦S. Let MR and MS denote respectively the matrix representations of the relations R and S. Then Example Solution: The matrices of the relation R and S are a shown in fig: 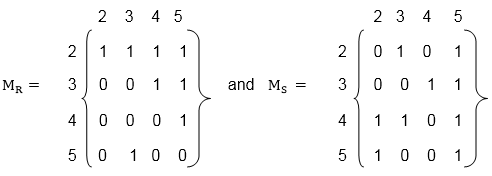 (i) To obtain the composition of relation R and S. First multiply MR with MS to obtain the matrix MR x MS as shown in fig: The non zero entries in the matrix MR x MS tells the elements related in RoS. So, 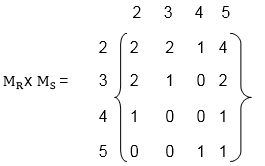
Hence the composition R o S of the relation R and S is (ii) First, multiply the matrix MR by itself, as shown in fig 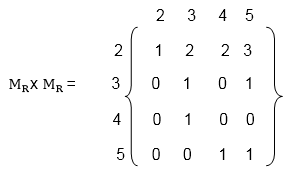
Hence the composition R o R of the relation R and S is (iii) Multiply the matrix MS with MR to obtain the matrix MS x MR as shown in fig: 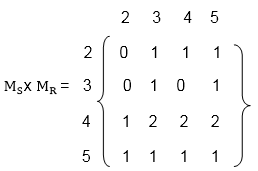
The non-zero entries in matrix MS x MR tells the elements related in S o R. Hence the composition S o R of the relation S and R is
Next TopicTypes of Relations
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










