Planar Graph:A graph is said to be planar if it can be drawn in a plane so that no edge cross. Example: The graph shown in fig is planar graph. 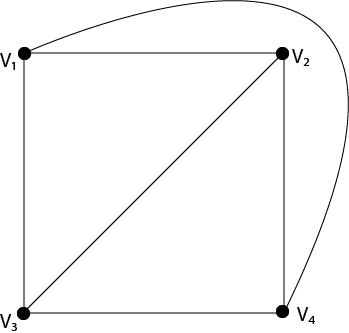 
Region of a Graph: Consider a planar graph G=(V,E).A region is defined to be an area of the plane that is bounded by edges and cannot be further subdivided. A planar graph divides the plans into one or more regions. One of these regions will be infinite. Finite Region: If the area of the region is finite, then that region is called a finite region. Infinite Region: If the area of the region is infinite, that region is called a infinite region. A planar graph has only one infinite region. Example: Consider the graph shown in Fig. Determine the number of regions, finite regions and an infinite region. 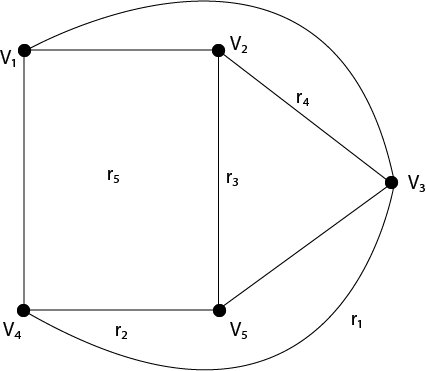
Solution: There are five regions in the above graph, i.e. r1,r2,r3,r4,r5. There are four finite regions in the graph, i.e., r2,r3,r4,r5. There is only one finite region, i.e., r1 Properties of Planar Graphs:
Example: Prove that complete graph K4 is planar. Solution: The complete graph K4 contains 4 vertices and 6 edges. We know that for a connected planar graph 3v-e≥6.Hence for K4, we have 3x4-6=6 which satisfies the property (3). Thus K4 is a planar graph. Hence Proved. Non-Planar Graph:A graph is said to be non planar if it cannot be drawn in a plane so that no edge cross. Example: The graphs shown in fig are non planar graphs. 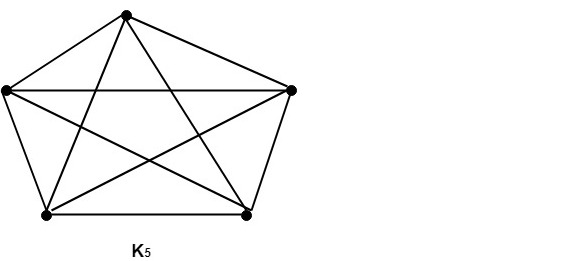
These graphs cannot be drawn in a plane so that no edges cross hence they are non-planar graphs. Properties of Non-Planar Graphs:A graph is non-planar if and only if it contains a subgraph homeomorphic to K5 or K3,3 Example1: Show that K5 is non-planar. Solution: The complete graph K5 contains 5 vertices and 10 edges. Now, for a connected planar graph 3v-e≥6. Hence, for K5, we have 3 x 5-10=5 (which does not satisfy property 3 because it must be greater than or equal to 6). Thus, K5 is a non-planar graph. Example2: Show that the graphs shown in fig are non-planar by finding a subgraph homeomorphic to K5 or K3,3. 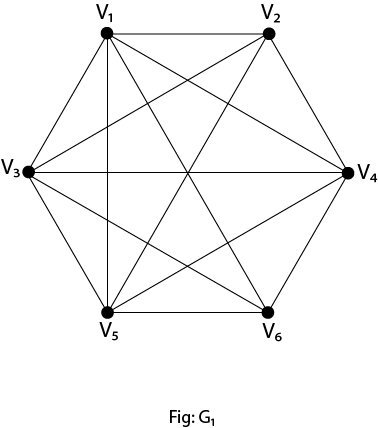 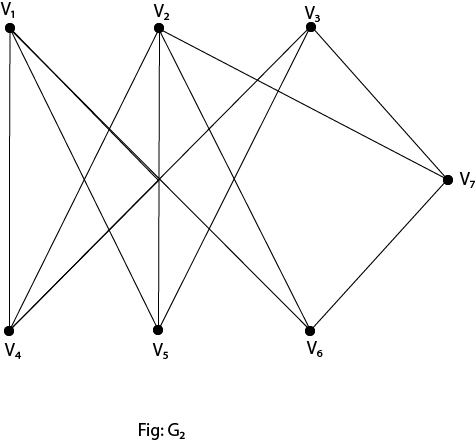
Solution: If we remove the edges (V1,V4),(V3,V4)and (V5,V4) the graph G1,becomes homeomorphic to K5.Hence it is non-planar. If we remove the edge V2,V7) the graph G2 becomes homeomorphic to K3,3.Hence it is a non-planar. Graph Coloring:Suppose that G= (V,E) is a graph with no multiple edges. A vertex coloring of G is an assignment of colors to the vertices of G such that adjacent vertices have different colors. A graph G is M-Colorable if there exists a coloring of G which uses M-Colors. Proper Coloring: A coloring is proper if any two adjacent vertices u and v have different colors otherwise it is called improper coloring. Example: Consider the following graph and color C={r, w, b, y}.Color the graph properly using all colors or fewer colors. 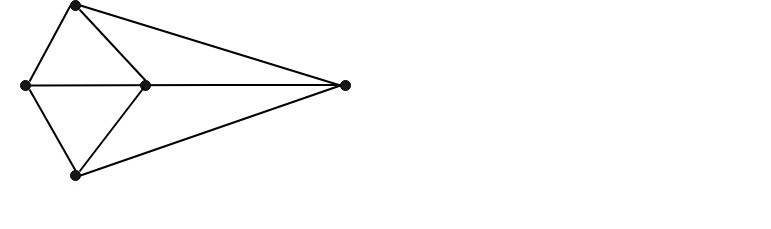
The graph shown in fig is a minimum 3-colorable, hence x(G)=3 Solution: Fig shows the graph properly colored with all the four colors. 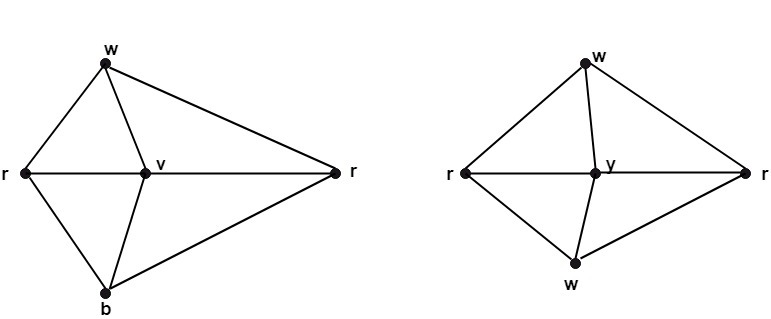
Fig shows the graph properly colored with three colors. 
Chromatic number of G: The minimum number of colors needed to produce a proper coloring of a graph G is called the chromatic number of G and is denoted by x(G). Example: The chromatic number of Kn is n. Solution: A coloring of Kn can be constructed using n colours by assigning different colors to each vertex. No two vertices can be assigned the same colors, since every two vertices of this graph are adjacent. Hence the chromatic number of Kn=n. Applications of Graph ColoringSome applications of graph coloring include:
State and prove Handshaking Theorem.Handshaking Theorem: The sum of degrees of all the vertices in a graph G is equal to twice the number of edges in the graph. Mathematically it can be stated as: ∑v∈Vdeg(v)=2e Proof: Let G = (V, E) be a graph where V = {v1,v2, . . . . . . . . . .} be the set of vertices and E = {e1,e2 . . . . . . . . . .} be the set of edges. We know that every edge lies between two vertices so it provides degree one to each vertex. Hence each edge contributes degree two for the graph. So the sum of degrees of all vertices is equal to twice the number of edges in G. Hence, ∑v∈Vdeg(v)=2e
Next TopicDijkstra's Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





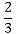 e.
e.




