Arguments in Discrete MathematicsIn discrete mathematics, the argument can be described as a part of philosophy and logical reasoning. It can also be used in mathematical proofs. In this section, we will show arguments in logical reasoning and in general life. In logical reasoning, mathematical logic is used to prove logical proof. The proof can be described as a type of valid argument that is used to determine the truth values (True or False) of mathematical statements. The arguments can be described as a series of statements or propositions. It usually has the premises and conclusion. The premises are used to show the rest statement, while the conclusion is used to describe the end statement. The premises will be represented by p1, p2, p3, ?, pk, and the conclusion or final statement will be represented by q. The final statement can be processed with the help of symbol "∴". The argument will be represented in the following form: If the statement of an argument is premises, in this case, premises can be used to provide support. If the statement of an argument is the conclusion, in this case, the conclusion is used to show that the premises are intended to provide support. In general terms, the goal of arguments is to persuade someone of something. If someone disagrees or have doubt about our viewpoint or claim, with the help of arguments, we have to convince him to agree with our viewpoint. For example: For starting the argument, we need a specific point of view on which the reader has some doubt. The reader must be convinced at the end of this argument, and they must no longer have any doubt on this view. The last or end statement is also known as the conclusion, and the remaining statements are also known as the premises. If we have to argue well, we have to put ourselves in the position of the reader and things about the doubt that the readers might have about our viewpoint. When we hear the word argument, we sometimes think it is quite aggressive and hostile, but it is not true. If an argument is good, it will be quite calm, fair-minded, and reasonable. Examples of ArgumentsExample 1: This argument is very common which is used by parents all the time for their children. It is using a technique known as rhetorical where we try to show that the reasoning of another person (in this example, the other person is son) is invalid when taken to its logical conclusion. In this example, the son is arguing with the parents: My friends are going for a picnic, so I also want to go. The parent shows that how the argument of a son fails. Types of ArgumentsThe arguments are basically of three types: Valid argument, Deductive arguments, and Inductive arguments. Valid ArgumentA valid argument can be described as an argument in which if all its premises are true, then the conclusion of that argument will also be true. If the true premise is contained in the valid arguments, the argument will be known as the sound. The arguments can either be sound or unsound and valid or invalid, and we have no middle ground to do this. Suppose the valid argument contains premises as p1, p2, p3, ..., pk and conclusion as q. Then the valid argument will be described as follows: For example: We can check the validity of an argument with the help of checking the critical row in the truth table. The critical row is a type of row where the true value is shown by all the premises, and these true values also correspond to the true value for the conclusion. Examples of Valid Arguments Example 1: We have to check whether the argument (p ∨ q, p → r, q → r, ∴ r) is valid or not. Solution: In this case, premises are shown by p ∨ q, p → r, q → r, and the conclusion is shown by r. This statement will be valid if all the premises are true and true premises also correspond to the true value of conclusion. To differentiate the premises and conclusion, we will use different colors. Grey color for the premises and red color for the conclusion. We will prove it with the help of a truth table, which is described as follows:
In this table, all the grey color shaded position contains the true value. That's why all these shaded rows are the critical rows, and these rows correspond to the true value for r. So in this table, if the premises (p ∨ q, p → r, q → r) are true, then the conclusion (r) is also true. Hence, the above argument (p ∨ q, p → r, q → r, ∴ r) is valid. Example 2: We have to check whether the argument (p → q, ∴ ∼ p → ∼ q) is valid or not. Solution: In this case, premises are shown by p → q, and conclusion is shown by ∼ p → ∼ q. This statement will be valid if all the premises are true and true premises also correspond to the true value of conclusion. To differentiate the premises and conclusion, we will use different colors. Grey color for the premises and red color for the conclusion. We will prove it with the help of a truth table, which is described as follows:
In this table, the critical rows are failed because, in the third row, the premise (p q) is true while the value of conclusion is false. Hence, the above argument is invalid. Example 3: We have to check whether the argument (p → q, q → r, ∴ p ∨ q → r) is valid or not. Solution: In this case, premises are shown by p → q, q → r, and conclusion is shown by p ∨ q → r. This statement will be valid if all the premises are true and true premises also correspond to the true value of conclusion. We will prove it with the help of a truth table, which is described as follows:
In this table, all the critical rows correspond to the true value for a conclusion. Hence, the argument (p → q, q → r, ∴ p ∨ q → r) is valid. In logic, the meaning of "valid" and "true" both are different. In the validity, we will check that whether the conclusion follows from premises, while in the truth, we will see whether the statements are making up an argument. On the basis of the truth value of premises, a false conclusion may be contained in the perfectly valid argument. Same as on the basis of the truth value of premises, a true conclusion may also be contained in the invalid argument. For example: In this example, we will take the above argument that is As we have seen in the above example 3 that this argument is perfectly valid. So we will assume p as "I sleep a lot", q as "I don't study a lot", and r as "I will do well in my exams". Hence, this statement will be translated as: "If I sleep a lot, then I don't study a lot. If I don't study a lot, then I will do well in my exams. Therefore, if I sleep a lot or don't study a lot, I will do well in my exams." We have seen that this argument is perfectly valid, but it is clearly not a true conclusion. Because with the help of first hypothesis, it is true, and the second hypothesis is false. That;s why the conclusion will also be false. Deductive ArgumentsIn discrete mathematics, the deductive argument is a type of argument in which if the premises have the true value, then the result of a conclusion will always be the true value. There will never be any case in which premises have the true value and generate a false value of conclusion. So we can say that the arguments which have a guarantee of premises success, in this case, the conclusion will be known as the deductive or valid argument. 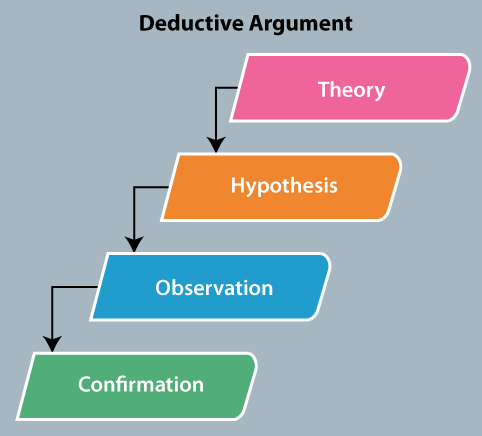
Example of Deductive argument: Example 1: Example 2: Example 3: The first two statements of all the examples are true, and that's why the conclusion will also be true. Example 4: Valid deductive argument In this example, we can see that the conclusion follows the word "So". If the above described two premises are true, it will provide the guarantee about truth of the conclusion. There is no way which can help us to decide that the two premises are true or not. So we are unable to say that the argument is deductively sound or not. It is one of them, but we don't know that it is which one. If we find out the given argument contains false premises and so is unsound, it will not be possible to change the fact that it is valid. Inductive ArgumentsThe inductive argument is intended with the help of the arguer. The argument will be known as strong if the true value is shown by all the premises, then it would not be possible that the conclusion is false. In the inductive argument, the truth of premises provides us a nice reason so that we can believe that the conclusion is probably true. In this section, we will use the term "strong" for a successful inductive argument, but actually, there is no standard term for this. If the inductive argument is not strong, it will be known as weak. But there is no sharp line that can differentiate the strong and weak. For example: Suppose there is an argument "dog biting me". This argument will be known as stronger if we are not able to think of any relevant conditions for why the next time will be different compared to the previous time. If there is a case that "I did walk by the dog", the argument will become more times stronger. If there is a case that "I have walked by the dog", the argument will become more time weaker. If the next time condition differs from the relevant conditions related to the past time, the argument will be weaker. For example, the dog has been sitting behind a closed door in the past time, but the gate will be opened the next time. 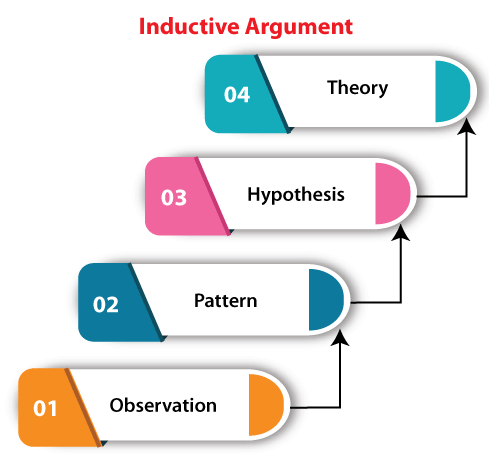
If we acquire some new premises (evidence), in this case, an inductive argument will be affected, but this same will not happen in a deductive argument. For example: Here we will describe a strong inductive argument like this: But the above inductive argument strength will be radically changed when the following premise is added: Example: The above argument is almost certainly true. This line of argument will readily accept by most of the persons. However, just like the deductive argument, we have noticed that it is not a matter of logical certainty, but a matter of probability. Because there is a possibility that aliens could come and destroy the sun. Due to this destroy, there will be no set or rise of the sun ever again. This situation is extremely unlikely, but it is not logically impossible. So the deductive argument seems stronger as compared to the inductive ones in the strict logical terms. Inductive arguments matter more, and there is a crucial advantage of inductive arguments. In our daily life, our almost decisions are taken with the help of inductive inferences like this: With the help of words used in an argument, we are not able to differentiate between inductive and deductive arguments. We can do this by knowing the intentions of arguer. It can be determined with the help of relationship between premises and conclusion believes by the arguer. The argument will be known as deductive if the arguer believes that the truth of a conclusion is definitely established by the truth of premises. The argument will be known as inductive if the arguer believes that the truth of premises provides us a nice reason so that we can believe that the conclusion is probably true. Suppose there are some persons who are accessing the quality of argument, and they don't have any information related to the intentions of arguer. In this case, they have to check for both arguments. Here we access the argument so that we can see whether it is inductively strong or deductively valid. 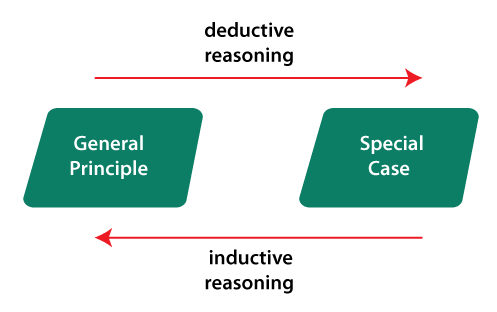
Importance of ArgumentsThe most important skill in daily life or discrete mathematics, and many more places, is the argument. If we do a master's degree in the art of persuasion, we are able to convince people very easily. Because of this skill, we will be very successful in our career, college, or school. Suppose we are very good at doing arguments and have convincing power, then we can persuade our parents, teacher, manager, boss, or leader of our viewpoint. In this case, we will be invincible. So we have realized that the power of argument is very huge. We should also know the difference between a good argument and a bad argument. We are able to see the good and bad arguments in our news channels, daily life, or at school conversations. In the case of critical thinking, an argument can be described as a basic task. Suppose a person doesn't have the skill of argument. In this case, advertisers or politicians are able to easily mislead him because they always try to persuade him to buy their products even if the product is not good or try to persuade him to vote for them Difference between Argument and FightingWhile watching sports analysis and political debates on news channels, many people sometimes get the impression that arguments are aggressive and hostile. They think their main goal is to defeat the opponent rather than persuade anyone. But it is not important that this is always true. In fact, an argument will be known as best if it comes from a place of friendship and sympathy. If the points of view of our friends and us are different, they will always try to explain the reasoning behind their view in a way that an understanding can be built. Due to this, a friendly debate or argument will be created. The most important skill that we should definitely learn and follow in our life is an argument. Whether it is personal or professional, we cannot avoid a certain amount of disagreement and conflict in our relationships. This conflict can be with your boss, employees, wife, parents, or with anyone. If we are unable to do argue with reason and logic, we will always end our argument with fighting. At the end of the argument, we must have an agreement. If there is no possibility of agreement, we should at least understand the reasons that why agreement is not possible. While, in case of fighting, we will express our emotions such as hurt, anger. At the time of fighting, we never care about the point of view of another person. In anger, we usually shout at the other person. In contrast, this problem can be resolved if we are able to do the right argument. In the case of fighting, the situations usually become worse. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









