The Pigeonhole Principle

If n pigeonholes are occupied by n+1 or more pigeons, then at least one pigeonhole is occupied by greater than one pigeon. Generalized pigeonhole principle is: - If n pigeonholes are occupied by kn+1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k+1 or more pigeons.

Example1: Find the minimum number of students in a class to be sure that three of them are born in the same month.

Solution: Here n = 12 months are the Pigeonholes
                    And k + 1 = 3
                    K = 2

Example2: Show that at least two people must have their birthday in the same month if 13 people are assembled in a room.

Solution: We assigned each person the month of the year on which he was born. Since there are 12 months in a year.

So, according to the pigeonhole principle, there must be at least two people assigned to the same month.

Inclusion-Exclusion Principle:

Let A₁,A₂......A_r be the subset of Universal set U. Then the number m of the element which do not appear in any subset A₁,A₂......A_r of U.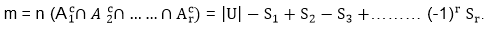

Example: Let U be the set of positive integer not exceeding 1000. Then |U|= 1000 Find |S| where S is the set of such integer which is not divisible by 3, 5 or 7?

Solution: Let A be the subset of integer which is divisible by 3
                Let B be the subset of integer which is divisible by 5
                Let C be the subset of integer which is divisible by 7

Then S = A^c ∩ B^c∩ C^c since each element of S is not divisible by 3, 5, or 7.

By Integer division,

          |A|= 1000/3 = 333
          |B|= 1000/5 = 200
          |C| = 1000/7 = 142
          |A∩B|=1000/15=66
          |B∩C|=1000/21=47
          |C∩A|=1000/35=28
          |A∩B∩C|=1000/105=9

Thus by Inclusion-Exclusion Principle

          |S|=1000-(333+200+142)+(66+47+28)-9
          |S|=1000-675+141-9=457