Inverse Function in Discrete mathematics

If there is a function f, then the inverse function can be indicated by f^-1. We can also call the constant function as an anti function because it is very easy to reverse this function into another function. In other words, we can say that if we have a function f that takes 'x to y', then inverse function f will take 'y to x'. Suppose there are an original function f and an inverse function f^-1. In case of the inverse function, the domain of f will become the range of the f^-1. Same as the range of f will become the domain of f^-1. We can get the graph of inverse function f^-1 with the help of replacing (x, y) with (y, x) with reference to line y = x. Here we should not get confused between -1 and the exponent or reciprocal because f^-1 is not the reciprocal of f. We will get the domain value x with the help of composition of the original function f and the reciprocal function f^-1 in the following way:

(f o f^-1) (x) = (f^-1 o f) (x) = x

If we have two inverse function f and g, then f(x) = y iff g(y) = x.

We had learned the use of an inverse sine function in trigonometry, where we use this function to determine the angle for which sine functions are able to generate the value. For example: sin^-1(1) = sin^-1(sin 90) = 90 degree. Here the value of sin 90 degree is 1.

Now we will learn about the definition of an inverse function, steps, graphs, and examples of the inverse function.

Definition Inverse function

A function will be known as an inverse function when each element in the domain x ∈ X must have a mapping with each and every element in the range y ∈ Y. We can also call this relation as an injunction relation or one-to-one relation. Suppose there is an inverse function f^-1 of the given function f in which the domain y ∈ Y is mapped with the distinct element x ∈ X in the codomain set. In that case, the relation with reference to function f will be known as the surjective function or onto function. Thus, those types of inverse functions, which is both one-to-one and surjective function, are known as the bijective function.

Suppose there is a function f with two sets X and Y. Here, set X is used to indicate the domain, and set Y is used to indicate codomain. This function will be invertible if we have another function g, whose domain is indicated by set Y, and its codomain is indicated by set X. The functions f and g can be indicated in the following way:

In the above type of situation, if the function f(x) is inverse, then the inverse of this function g(x) will always be unique. The two given functions will be known as inverse of each other if the result of composition of two functions f(x) and g(x) will be an identity function f(g(x)) = x. Suppose we have an original function f and an inverse function f^-1. In case of the inverse function, the domain of f will become the range of the f^-1. Same as the range of f will become the domain of f^-1.

Note:

When the relation is developed at the time of interchanging the independent variable with those types of variables which is dependent on a specific equation, in this case, the generated inverse may or may not be a function.
When we do the inverse of a function, and its inverse will be itself, then this type of function will be known as inverse function, which is indicated by f^-1(x).

Steps to find an Inverse function

We can easily determine the inverse function with the help of following sequence of steps. Here we will assume a function f where f(x) = ax + b, and then try to determine the inverse of this function with the help of following steps:

For the above function f(x) = ax + b, we will replace f(x) = y, and then obtain y = ax + b.
In this function, we will interchange y with x and x with y. After interchanging, y = ax + b will become x = ay + b.
Now we will solve this expression x = ay + b for y. After solve this expression, we will get y = (x - b) / a.
Lastly, we will replace y = f-1(x), and then we will have f-1(x) = (x - b) / a.

Find the Inverse of Function

In the process of finding the inverse, we generally do the swapping of coordinates x and y. It is not compulsory that this newly created inverse will be a function, but this inverse must be a relation. The newly created inverse will be indicated as a function if and only if there is a case where the original function is one to one function because we know that the inverse of injective function will always be a function. A function will be known as a one-to-one function if each element of one set has a mapping with a unique element of another set.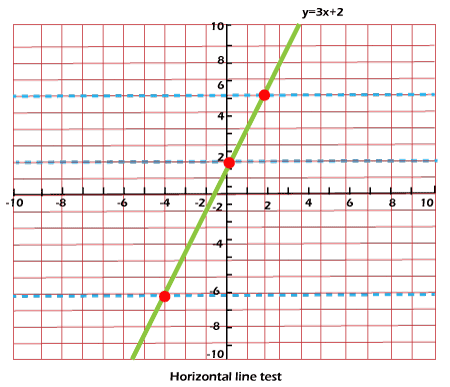

Inverse Function in Discrete mathematics

We can find whether the given function is one to one function or an injective function with the help of a horizontal line test. The function will be one-to-one, and its inverse will also be a function if there is a single region in which the horizontal line intersects the original function.

Types of Inverse function

We have various types of inverse functions. Some of them are: Inverse of log functions, inverse of rational functions, inverse of trigonometric functions, and inverse of hyperbolic functions. The inverse of some functions is described as follows:

Function	Inverse of function	Comment
*	/
+	-
x²	√y	Here, x and y are greater than or equal to 0.
xⁿ	y^1/n	Here, n is not equal to 0.
1/x	1/y	Here, x and y are not equal to 0.
cos(x)	Cos^-1(y)	0 to π
Sin(x)	Sin^-1(y)	-π/2 to + π/2
Tan(x)	Tan^-1(y)	-π/2 to + π/2
a^x	log a(y)	y and a>0
e^x	In(y)	y>0

Inverse of Trigonometric Functions

We can also call inverse trigonometric as an arc function. This is because the inverse trigonometric function is used to generate the length of an arc, which is used to get the particular value. We have total 6 types of inverse trigonometric functions. These functions are arcsecant (sec^-1), arccotangent(cot^-1), arcsine(sin^-1), arccosecant(cos^-1), arccosine(cos^-1), and arctangent(tan^-1).

Inverse Relation Function

The inverse relation must be in the form f(x) = P(x) /Q(x) where Q(x) is not equal to 0. We will use the following steps to determine the inverse of a relational function.

Step 1: In this step, we will replace f(x) = y.

Step 2: After that, we will interchange x and y.

Step 3: Now, we will solve for y in terms of x.

Step 4: Lastly, we will replace y with f^-1(x). From this, we will obtain the inverse of the function.

Inverse Hyperbolic Functions

Same as the inverse trigonometric function, this function is also the inverse of hyperbolic functions. We have total 6 types of inverse hyperbolic functions. These functions are: csch^-1, sech^-1, cosh^-1, coth^-1, sinh^-1, and tanh^-1.

Inverse Exponential Function and Inverse Logarithmic Functions

The natural log functions can be described as an inverse of exponential functions. Now we will understand the logarithm functions and inverse exponential function with the help of following example. We will also learn how we can solve these types of similar questions with the help of this example.

Finding Inverse function by Algebra

Here we will try to find the inverse function with the help of algebra. For this, we will put y for f(x) and then solve for x. The description of this is described in the following table:

Function is:	f(x)	=	2x+3
We will put 'y' for 'f(x)'	Y	=	2x+3
Now we will subtract 3 from both the sides	y-3	=	2x
Then we will divide both sides by 2.	(y-3) /2	=	x
Now we will swap x with y and y with x.	X	=	(y-3) /2
So the solution (put "f^-1(y)" for "x") is:	f^-1(y)	=	(y-3) /2

Graph of an Inverse function

The inverse function can be described as a reflection of the original function, which contains the reference of line y = x, and we can get it by replacing (x, y) with (y, x). The graph of the line y = x will be passed through the origin and must have the slope value 1. We can represent it in the following way:

y = f^-1(x)

It is equal to the following:

x = f(y)

The above relation is the same as y = f(x). Here f(x) is used to indicate the graph of f, but in this relation, the place of x and y is reversed. If we draw the graph of inverse function f^-1, we will swap the positions of x and y in axes.

If we have the graph of two functions, in this case, we can easily find out whether they are inverse of each other. Two functions will be inverse to each other if and only if the graphs of two functions are symmetric with reference to the line y = x. We confidently say this fact because we know that when (x, y) lies on the function, then (y, x) lies on its inverse function.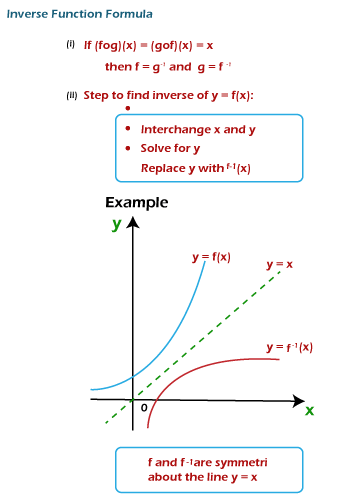

Examples of Inverse function

There are various examples of inverse functions. Some of the examples of inverse function are described as follows:

Example 1: In this example, we will consider two functions, f and g. Where f(x) = 2x + 3 and g(x) = (x-3) / 2. Now we have to determine the inverse of these functions with the help of formula of an inverse function.

Solution:

Here we have to show that (f o g)(x) = (g o f)(x) = x.

To prove this, first we will take the left side part, which is described as follows:

(f o g)(x) = f (g(x))

= f ((x-3) /2)

= 2 ((x-3) /2) + 3 (2 is cancelled by the 2)

= x-3+3

= x

Now we will take the right side of part and try to prove it like this:

(g o f)(x) = g (f(x))

= g(2x+3)

= (2x +3 -3) /2

= 2x /2

= x

Through this, we can see that (f o g)(x) = (g o f)(x) = x.

With the help of inverse formula, we can say that f and g are inverses of each other.

Hence, we have proved that f = g^-1 and g = f^-1.

Example 2: In this example, we have a function f. Where f(a) = 4a+1 /3a-2. Now we have to determine the inverse function with the help of formula of an inverse function.

Solution:

Here we will use the formula of inverse function to determine the inverse function.

As we know that the given function is:

b = (4a+1) / (3a-2)

When we interchange x and y, we will get the following:

a = (4b+1) / (3b-2)

Now we will solve the expression for y. For this, we will multiply both sides by (3b- 2) and get the following:

a(3b - 2) = 4b+1

3ab - 2a = 4b+1

3ab - 4b = 2a+1

b(3a - 4) = 2a+1

b = 2a+1 /3a-4