Difference between Function and Relation in Discrete Mathematics

The function and relation are very much similar to each other. To learn the difference between relation and function, we have to first learn about the function and relation, and after that, we are able to learn the difference between them.

Relation

In discrete mathematics, the relation can be described as a collection of ordered pairs. It is used to relate an object from one set to the other set, and the sets must be non-empty. The relation can contain two or more than two sets. Suppose there are two sets, A and B for instance. Set A contains an object a, and set B contains an object b. The objects will be related to each other if there is a relation of ordered pair (a, b). With the help of a Cartesian product of subsets, the relation R can be formed.

Now we will assume the two arbitrary sets A and B. The Cartesian product of A and B can be described as the set of ordered pairs (a, b), where a ∈ A and b ∈ B. The product of A and B is designated as A cross B. With the help of definition, we will get the following:

The Cartesian product is able to deal with the ordered pairs, which is why it is important to notice the order in which sets are considered. Now we will use the n(A) to represent the number of elements in set A, which is described as follows:

Types of relations:

In discrete mathematics, the relation can be of various types, and we will differentiate the relations on the basis of defining a connection between the sets.

Empty relation:

A relation will be known as empty relation if the elements of set have no relation with each other. The empty relation is described as follows:

Universal Relation:

In this relation, every element of set A has a relation with every element of set B. That's why this relation is also called a universal relation, and the universal relation and empty relation are also known as the trivial relation.

Identity Relation:

In the identity relation, every element of A has a relation to itself only. The identity relation is described as follows:

Inverse Relation:

Assume that there are two sets, set A and set B, and they have a relation from A to B. This relation will be described as R∈ A � B. The inverse relation will be obtained when we replace the first element of each pair with the second element in a set. The inverse relation is described as follows:

Reflexive Relation:

A relation will be known as reflexive relative if every element of set A is related to itself. The word reflexive means that in a set, the image of every element has its own reflection.

Symmetric Relation:

Suppose there are two elements in a set A, i.e., a, b. The relation R on a set A will be called symmetric relation if element 'a' has relation with 'b' is true, then 'b' has a relation with 'a' will also be true. The symmetric relation is described as follows:

Transitive Relation:

Suppose there are three elements in a set A, i.e., a, b, and c. The relation R on a set A will be known as transitive relation if 'a' has a relation with 'b' and 'b' has a relation with 'c', then 'a' will be also has a relation with 'c'. The transitive relation is described as follows:

Equivalence Relation:

A relation will be known as equivalence relation if it satisfies the properties of symmetric, transitive, and reflexive.

Note: All relations are not functions, but all functions are relations.

Example of Relation:

We will take the real-life example to understand the concept relation more. Suppose we are going to make a blanket. For this, we need the fabric, which will help to build a blanket. We will make a blanket with the help of sewing together swatches of fabric. For fabric, we will go to shore and see the sale on these swatches. We don't know that how much fabric we need to buy one, two or three, and without knowing, we buy three swatches at the cost $4.00. After that cost, if we want to buy swatches, each swatch costs an additional $2.00. The number of swatches we buy and the amount of money we spend are related to each other. This can be known as an example of a relation.

There are two sets of elements in a relation called input and output, which are related to each other in some way. In our example, the input will be described as a cost, and the output will be described as the number of swatches. The relation can also be represented with the help of ordered pairs like this:

That means when we have 4 as an input in the above relation, we have 1, 2, or 3 as an output. This relation shows that if we spend $4, we are able to get 1, 2, or 3 swatches of fabric. Similarly, if we have 8 as an input, then we have 5 as an output. That means if we spend $8 to buy the swatches, we will get 5 swatches of fabric.

Functions:

The set of input elements has a relation with the set of output elements, and that relation is known as the function. In the function, for each and every element in set A, there will be only one output element in set B. For example: Suppose there are two sets: set A and set B. Both the sets are connected with each other with the help of some way, i.e., elements of given set A has a relation with the one element of given set B or all elements of set A has a relation with only one element of set B. So we can say this type of relation is a function. Using this example, we have cleared that set A and set B in a function cannot have one-to-many relations. In order to quantify as a function, we need to satisfy two conditions, which are described as follows:

• In the first condition, each and every a ∈ A must have a connection with b ∈ B. That means the domain of function f must be A and not a subset of A.
• In the second condition, there is a requirement of uniqueness that is going to be expressed as follows:

Types of Functions

In discrete mathematics, the functions can be of various types. Here we will describe the functions in terms of relations, which are shown as follows:

One-to-one Function:

One to one function can also be called the injective function. A function will be known as one-to-one if one element of the domain set is connected with the one element of a co-domain set. We can also write one to one as 1-1. In the one to one function, the answers never repeat.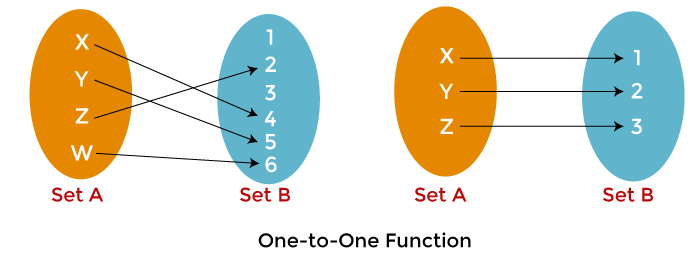

In the above image, we have two sets: Set A and Set B. The domain will be described by set A, and co-domain B will be described by set B. Here we can see that each and every element of Set A in image 1 and image 2 has a connection with a unique element of Set B. In image 1, X is connected with 4, Y is connected with 5, Z is connected with 2, and W is connected with 6. The same thing happens in image 2. That's why this function is known as one to one.

Example 1:

Here we will assume that there is a function f(x) = x - 4. Prove that this function is one to one function or not.

Solution:

If x = 1, then f(1) = -3

If x = 5 then f(5) = 2

If x = 7 then f(7) = 3

If x = 19 then f(19) = 15

Here we can see that the given function generates different outputs for every input value. That's why the function f(x) = x - 4 can be called one to one function.

Example 2:

Here we will assume that there is a function f(x) = x². Prove that this function is one to one function or not.

Solution:

If x = 3, then f(3) = 6

If x = -3 then f(-3) = 6

Here we can see that the given function generates the same answer 6 for value 3 and -3. That's why the function f(x) = x² cannot be called one to one function.

Many-to-one Function:

A function will be known as many to one function if more than one element of a domain set is connected with the same element of a co-domain set. That means a single element of co-domain can have connection with more than one element of the domain. The many to one function always contains repeated answers.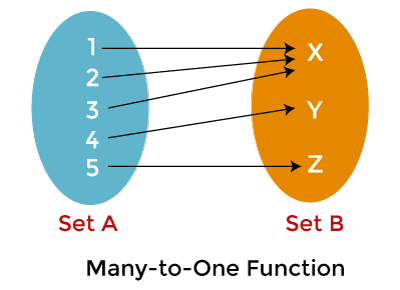

In the above image, we have two sets: Set A and Set B. The domain is described by set A, and the co-domain is described by set B. This image shows that many elements of Set A are mapped with a single element of Set B. Elements 1, 2, and 3 are connected with the same element X. That's why this function is many to one.

Example:

We will assume that there is a function f(x) = x². Prove that this function is many to one function or not.

Solution:

If x = 2, then f(2) = 4

If x = -2 then f(-2) = 4

Here we can see that the given function generates the same answer 4 for value 2 and -2. So we can say that the function f(x) = x2 is many to one function because, for the different values, this function generates the same answers.

Onto Function:

Onto function is also known as the Surjective function. A function will be known as a onto function if every element of a co-domain set is connected with at least one or more than one element of a domain set.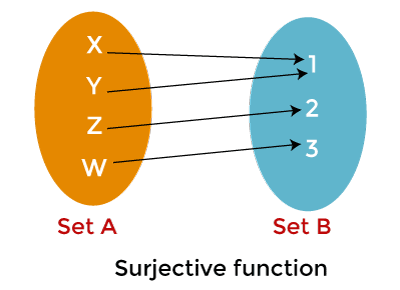

In the above image, we have two sets: Set A and Set B. Here we can see that each element of Set B is mapped with at least one element of Set A. The elements X and Y in set A are connected with element 1 in set B, Z is connected with 2, and W is connected with 3. That's why the above function is onto.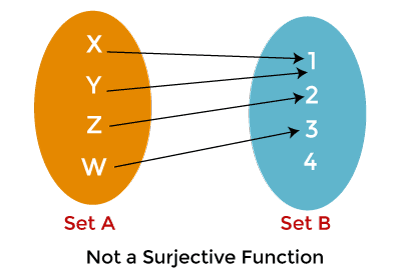

In this image, we again have two sets. Here we can see that one element of set B is not connected with any element of set A. Same as the above image, element X and Y are connected with 1, Z is connected with 2, W is connected with 3, but element 4 in set B has no connection with set A. That's why we can say that the above function is not onto.

Example:

Suppose there is a function f which contains two sets A and B. where A = {2, 5, 7, 8}, B = {4, 9}, and f = {(2, 4), (5, 9), (7, 4), (8, 9)}. Now prove that this function is onto function.

Solution:

So from the question we have

A = {2, 5, 7, 8}

B = {4, 9}

f = {(2, 4), (5, 9), (7, 4), (8, 9)}

So, all the elements on set 'B' have a domain element on set 'A'. That means elements on set 'A' 2, 5, 7, and 8 contain the same range with elements on set 'B' 4, and 9, respectively. That's why we can say that function f: A → B is an onto function.

One to one correspondence Function

The one to one correspondence function can also be called the Bijective function. This function is a combination of injective function (one to one function) and surjective function (onto function). A function will be known as one-to-one correspondence function if every element of the domain set is connected with exactly one element of a co-domain set and vice versa. In the bijective function, from set A to set B, there is an inverse function from set B to set A. In the bijective function, every element of the set has a relation with itself.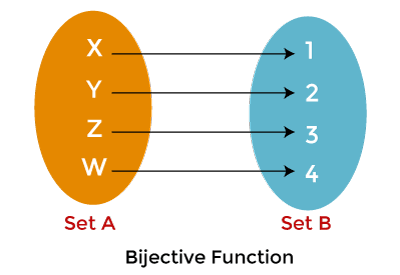

The above image shows that every element of co-domain (Set B) has been related to the distinct element of domain (Set A). The element X is connected with element 1, Y is connected with 2, Z is connected with 3, and W is connected with 4. That's why the above function is one to one correspondence.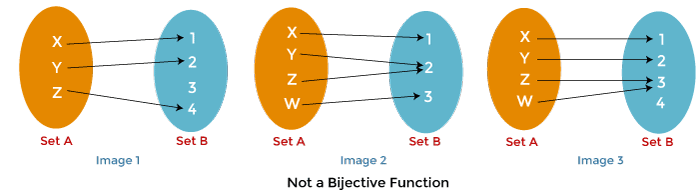

The above image shows that the function is not one to one correspondence because there are some elements in set B in image 1, don't have a connection with the element of set A. Element 3 in set B has no connection with any element of set A. In the images 2, and 3, more than one element of set A has a connection with one element of set B. The element Y, Z in image 2 has the same value 2. Same as in image 3, the elements Z, W has the same value 3. That's why we can say that the above function is not a bijective function.

There are four conditions that are required to satisfy the bijective function:

• Every element of set A will be connected with an element of set B.
• On a set A, the element is able to only pair with one element of set B.
• Each and every element of set B will be connected with an element of set A.
• On set B, the element can only be connected with one element of set A.

Properties of Bijective function

The bijective function has a lot of properties, which are described as follows:

• In the bijective function, there will be the same number of elements in the domain and co-domain sets.
• There will be the same amount between the co-domain and range of bijective function.
• There will be an inverse function in the bijective function.
• The constant function and the bijective function cannot be the same.
• If a graph is represented with the help of a bijective function, then it will always be a straight line.
• A lot of properties are followed by the bijective function such as symmetric, transitive and reflexive.

Example:

Suppose there is a function f which contains two sets A and B. where A = {2, 3, 4, 5}, B = {u, v, x, y}, and f: A → B. Now prove that this function is a bijective function.

Solution:

For this,

f(2) = u

f(3) = x

f(4) = v

f(5) = y

So the function f is onto and also one to one. That's why this function is a bijective function.

Other types of Functions:

There are many other types of functions, which are described as follows:

Constant Function: The constant function can be written as f(x) = c.

Inverse Function: The inverse function can be written as f^-1(x).

Absolute Value Function: The inverse value function can be written as f(x) = |x|.

Identity Function: The identity function can be written as f(x) = x.

Linear Function: The linear function can be written as f(x) = mx + c.

Example of Function:

Same as an example of relation, in this example, we will again make a blanket. But this time, when we go to the store to buy the swatches, on that day, there is no sale on the store. That's why the costs of swatches are $2 per piece. Because of this, the relation between input and output is going to be different. This relation can also be represented with the help of ordered pairs like this:

In our example, the input is also described as a cost, and the output is also described as the number of swatches, just like the example of a relation. However, this relation is called a special type of relation. There is the main difference between this example and the example we described in the relation, which we can explain with the help of first three ordered pairs in the relation.

When there was a sale on the swatches, we saw that the first three ordered pairs contained the same input with different outputs in the first relation. But if we consider this relation when there is no sale, we will see that each input contains only one output. In this case, when there is only one output for one input, the relation is known as the function. So with the help of this example, we can say that the number of swatches we buy is a function of the cost.

Difference between Function and Relation

The relation and function both are different concepts. The relation cannot be function, but all the functions are relations. The relation and function have the main difference, i.e., a relation is able to generate many outputs for at least one input, but in the case of function, it can only generate one output for every input. This factor is very basic to differentiate between them. For example: Here, we will assume that there is a student who collected some data in a math class. The table of data is described as follows:

In the above table, we are able to see the two places with more than one output (12, 72) for one input (5).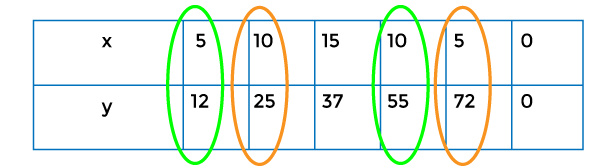

That's why the above set of ordered pairs show a relation, and it is not a function.

A relation can be described as a group of ordered pairs of elements, and it can be referred to as two-place relation or dyadic relation. The relation is also a subset of the Cartesian product. In order to form the model concepts, the relation is used. Relations provide us a sense of meaning such as "is equal to", "greater than", or "divides".

The function can be described as an ordered triple set, which contains A, B and F. In which A is used to represent the domain, B is used to represent the co-domain, and F is used to represent the set of ordered pairs. The primary element of each ordered pair comes from set A, the second element of this ordered pair comes from the co-domain (Set B), and it goes along with the help of necessary conditions. The one many relationships will not be contained by the function, which means one object cannot have a connection with many objects. The function will contain the many one relationships that mean many objects can have a connection with the one object.

The set of real numbers is contained by the domain and co-domain both. The property of items will be shown with the help of relations. Here some things are linked in some way. That's the reason it is known as the "relation". It doesn't imply that we don't have any in-between which can be used to distinguish between function and relation.

An item can be a function used to take a mixture of two-argument values that will generate a single output. The relation and function have one more difference, i.e., the function must contain a domain, which produces the outcome from the Cartesian product of two or more than two sets, but it is not compulsory that the relation will also generate the same things. Each input of two given sets in a function will generate only a single output. The relationship between the input elements and output elements will be represented with the help of relation.

We have listened to the term that all the relations are not function, but all the functions are relation. But now we will describe it in detail like this:

A function can be described as an ordered pair which generates only one value of b for every a's value. The relation can be described as any set of ordered pairs. Suppose there are set of ordered pairs (relation) and also have one value of b for every a. In this case, the relation is a function. So we can say that a function is a set of ordered pairs that generates only a single b's value for every a's value. If there is a case when we have only one value of b for every a, then the relation can always be a function.

In contrast to this, if the set of ordered pairs (relation) contain more than one output (b) for an input (a), in this case, the relation is not function. This will prove that the second statement, which says that all relations are not function will be true. We will also prove both the statement with the help of following examples. In the first example, the table is used to describe the relation that is a function. In the second example, the table is used to describe the relation that is not a function. In the third example, we have to determine that the given relation is a function or not.

Example 1: A relation that is a function is described as follows:

Here for every value of A, there is one value of B. That means 0 contains 0, 1 contains 1, 2 contains 2, and 3 contains 3. That's why this relation is a function.

Example 2: A relation that is not a function is described as follows:

Here for an input value of A, there is more than one value of B. That means for value 2, there are values 2 and 1. That's why this relation is not a function.

Example 3: We have to determine that the following relation is a function or not.

In the above table, every value of set A contains single value of B. That's why the above relation is a function.