Rolle's Mean Value Theorem

Roll's theorem is a special case of the mean value theorem. Rolle's theorem states that if a f be a real valued function defined on the closed interval [a, b] where (a?x ?b) and differentiable in open interval ]a,b[where (a < x< b), and f (a) = f(b) then there is at least one value c in ]a,b[for which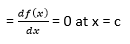

Proof of Rolle's mean value theorem

If the function f is continuous in [a,b] and differentiable in open interval ]a,b[, with f(a) = f (b)=0 then there exist c in (a,b) where f' (c) = 0.

Proof

Let's suppose the two cases that could happen:

Case 1:

f(x) = 0 for all x in [a,b].

In the above case, the value that exists between a and b can serve as the c (mentioned in the equation), as the function is constant on [a,b], and as we know, the derivatives of constant functions are always zero.

Case 2:

f(x) = ? 0 for x in open interval ]a,b[

We know by the extreme value theorem that f accomplishes both its absolute minimum and maximum values somewhere on [a,b].

As we discussed above, f(a) = f (b)=0, and that in this case, f(x) is not equal to zero for some x in open interval ]a,b[. Therefore, f will have either positive absolute maximum value at some C_max in closed interval [a,b] or a negative absolute minimum values in closed interval some C_min in ]a,b[ or both.

Take c to be either C_max or C_min, depending on which you have

In the open interval ]a,b[ contains c, and either;

• f(c) ? f(x) for all x in open interval in ]a,b[; or
• f(c) ? f(x) for all x in open interval in ]a,b[.

It means f has a local extremum at c.

As f is also differentiable at c, Fermat's theorem applies and concludes that

f' (c) = 0

Let's understand this concept with the help of an example

Example 1:

Verify Rolle's theorem for the function y = x² + 3, a = - 2 and b = 2

Solution:

We know the statement of the Rolle's theorem, the function y = = x² + 3 is continuous in [-2 ,2] and differentiable in (-2,2)

Given;

F(x) = x² + 3

F (-2) = (-2)² + 3 = 4 + 3 = 7

F (2) = (2)² + 3 = 4 + 3 = 7

Thus,

F (-2) = F (2)

Therefore, the value of f (x) at -2 and 2 coincide

Now,

F' (x) = 2x

At c = 0,

F'(c) = 2 (0), where c=0 ∈ (-2,2)

Example 2:

For all second-degree polynomials with y = mx² + nx + k, it is seen that the Rolle's point is at c = 0. Also, the value of k is zero. Then find the value of n?

Solution:

Given;

K = 0

We have to rewrite the function to get

y = mx² + nx

Now, differentiating the function yields

Y' = 2mx + n = 0

Equating it to zero we get the Rolle's point which is also zero

2m(0) + = 0

n= 0

Geometric Interpretation

The geometrical meaning of Rolle's mean value theorem states that the curve y = f (x) is continuous between x = a and x = b. At every point of time, within the interval, it is possible to make a tangent and ordinates corresponding to the abscissa and are equal then exists at least one tangent to the curve which is parallel to the x-axis.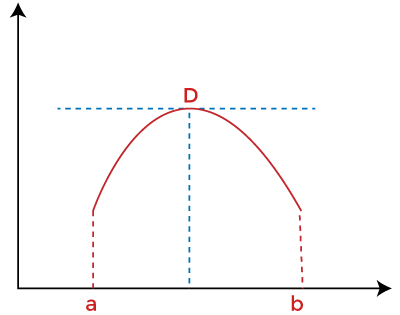

Algebraically, Rolle's theorem states that if f (x) is showing a polynomial function in x and the two roots of the equation f (x) = 0 and x = a and x = b, then there exists at least one root of the equation f (x) = 0 lying between these values.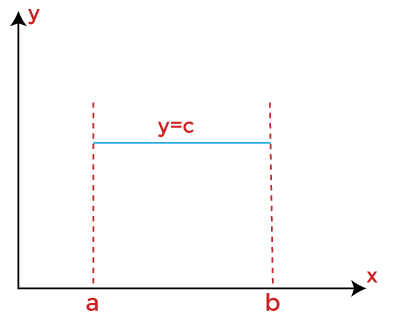

Questions based on Rolle's Theorem

Examples 1

Verify Rolle's theorem for the function y = x² + 5, a = - 3 and b = 3

Solution:

We know the statement of the Rolle's theorem, the function y = = x² + 5 is continuous in [-3 ,3] and differentiable in (-3,3)

Given;

F(x) = x² + 5

F (-3) = (-3)² + 5 = 9 + 5 = 14

F (3) = (3)² + 5 = 9 + 5 = 14

Thus,

F (-3) = F (3)

Therefore, the value of f (x) at -3 and 3 coincide

Now,

F' (x) = 2x

At c = 0,

F'(c) = 3 (0), where c=0 ∈ (-3,3)

Example 2:

For all second-degree polynomials with y = ix² + jx + k, it is seen that the Rolle's point is at c = 0. Also, the value of k is zero. Then find the value of j?

Solution:

Given;

K = 0

We have to rewrite the function to get

y = ix² + jx

Now, differentiating the function yields

Y' = 2ix + j = 0

Equating it to zero we get the Rolle's point which is also zero

2i(0) + j = 0

J = 0